HNU数据结构与算法分析-实验四--- 对输入的两棵二叉树A和B,判断B是不是A的子树
本篇代码包括实验报告与源码,
实验报告最终得分为94/100
下面我将先给出实验报告,再附上源码,
其中算法的精髓我在报告中彩色标注了,如果有不理解的同学可以先看看,我觉得应该会有帮助
最后,如果感觉有帮助的话还请点个赞,你的重要支持是我继续创作的动力。
【原题目】
【问题描述】
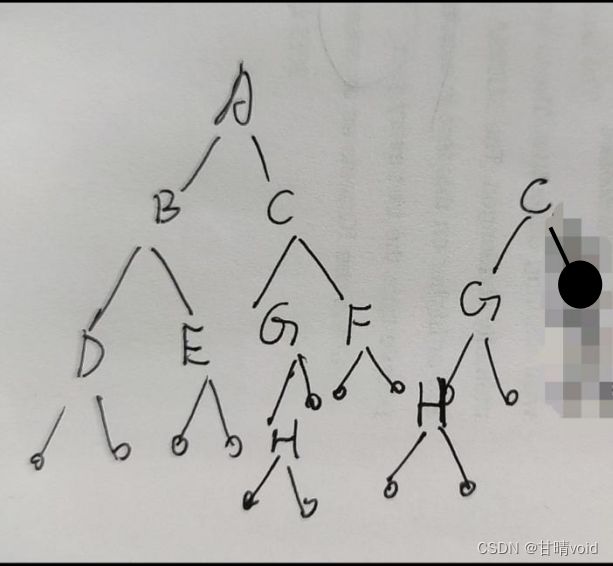
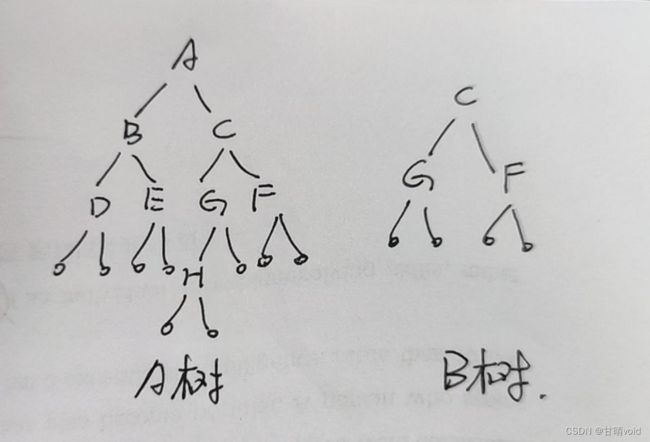
基于实验三设计的ADT,对输入的两棵二叉树A和B,判断B是不是A的子树。设T是一棵树,a是T中的一个顶点,由a以及a的所有后裔(后代)导出的子图称为树T的子树。如图:二叉树B就是二叉树A的一棵子树,而二叉树C不是二叉树A的子树。
【输入形式】
每个输入文件的第一行为二叉树A的前序遍历顺序表示法(N≤30)。二叉树B的前序遍历顺序表示法。
注意:用“#”代表空指针NULL。
【输出形式】
yes 代表二叉树B就是二叉树A的一棵子树。
no 代表二叉树B不是二叉树A的一棵子树。
【样例输入1】
AB##C##
AB##C##
【样例输出1】
yes
【样例说明1】
二叉树B是二叉树A的一棵子树
【样例输入2】
ABD##E##CGH###F##
CGH####
【样例输出2】
no
【样例说明2】
二叉树B不是二叉树A的一棵子树
【样例输入3】
ABD##E##CGH###F##
CG##F##
【样例输出3】
no
【样例说明3】
二叉树B不是二叉树A的一棵子树
【样例输入4】
ABD##E##CGH###F##
CGH###F##
【样例输出4】
yes
【样例说明4】
二叉树B是二叉树A的一棵子树
【评分标准】
源代码请提交工程压缩包,压缩包内至少包含以下三个文件:
1)XXX.h:二叉树ADT的定义和声明
2)XXX.h:二叉树ADT的实现
3)XXXXX.cpp:主程序
(要求基于ADT实现,否则计0分。)
【实验报告】
目录
1.问题分析
l1.1处理的对象(数据)
l1.2实现的功能
l1.3处理后的结果如何显示
l1.4请用题目中样例,详细给出样例求解过程。
2.数据结构和算法设计
2.1抽象数据类型设计
2.2物理数据对象设计(不用给出基本操作的实现)
2.3算法思想的设计
2.4关键功能的算法步骤(不能用源码)
3. 算法性能分析
3.1时间复杂度
3.2空间复杂度
4.不足与反思
【正文】
1.问题分析
l1.1处理的对象(数据)
处理的对象为用字符表示的前序遍历二叉树,每个输入文件的第一行为二叉树A的前序遍历顺序表示法(N≤30)。第二行为二叉树B的前序遍历顺序表示法。其中用“#”代表空指针NULL。
l1.2实现的功能
对输入的两棵二叉树A和B,判断B是不是A的子树l
1.3处理后的结果如何显示
yes 代表二叉树B就是二叉树A的一棵子树。
no 代表二叉树B不是二叉树A的一棵子树。
1.4请用题目中样例,详细给出样例求解过程。
【样例输入1】
AB##C##
AB##C##
- 通过前序遍历读入树的各节点,存入树结构中;
- 通过前序遍历在A树中寻找B树的根节点 ,找到为A;
- 通过前序遍历,分别将A中的A和B中的A的子树分别存入容器中;
- 比较容器内元素个数,发现7==7,即元素个数相同;
- 逐个比较容器内各元素的值,发现全部相同,返回结果yes。
【样例输入2】
ABD##E##CGH###F##
CGH####
1、通过前序遍历读入树的各节点,存入树结构中;
2、通过前序遍历在A树中寻找B树的根节点 ,找到为C;
3、通过前序遍历,分别将A中的C和B中的C的子树分别存入容器中;
4、比较容器内元素个数,发现9!=7,即元素个数不同,返回结果no;
【样例输入3】
ABD##E##CGH###F##
CG##F##
1、通过前序遍历读入树的各节点,存入树结构中;
2、通过前序遍历在A树中寻找B树的根节点 ,找到为C;
3、通过前序遍历,分别将A中的C和B中的C的子树分别存入容器中;
4、比较容器内元素个数,发现9!=7,即元素个数不同,返回结果no;
2.数据结构和算法设计
2.1抽象数据类型设计
template
class BinNode//结点类
{
private:
BinNode*lc;//左孩子
BinNode*rc;//右孩子
E elem;
public:
BinNode();//默认构造函数,设置左右孩子为空
BinNode(E tmp, BinNode*l=NULL, BinNode*r=NULL);
//带参构造函数
BinNode*left();//返回左孩子
BinNode*right();//返回右孩子
void setLeft(BinNode*l);//设置左孩子
void setRight(BinNode*r);//设置右孩子
void setValue(E tmp);//设置当前结点的值
E getValue();//获得当前结点的值
};
template
class BinTree//二叉树类
{
private:
BinNode
void clear(BinNode
public:
BinTree();//默认构造函数
~BinTree();//析构函数
bool BinTreeEmpty();//判断二叉树是否为空
BinNode
void setRoot(BinNode
//下面的函数是对外的函数,所以内部还会有一些同名的函数,但是参数列表不一样,实现数据的封装,外部的调用不会涉及到内部的数据对象
void preOrder(void(*visit)(BinNode
//先序遍历,传入相对应的访问函数即可对该当前结点实现不同功能的访问(本程序为输出)
bool find(E e);//查找二叉树中是否存在名为e的结点
BinNode
//查找二叉树中是否含有某个名为e的结点
};
2.2物理数据对象设计(不用给出基本操作的实现)
//BinaryTreeNode二叉树的节点的实现
BinNode
BinNode
//模板函数的默认参数似乎必须在第一次声明的时候给出,也就是说,这里不能有两个=NULL,详情参见https://blog.csdn.net/u013457310/article/details/89510406
BinNode
BinNode
void BinNode
void BinNode
void BinNode
E BinNode
//BinaryTree二叉树的实现
BinNode
BinTree
BinTree
BinNode
void BinTree
//下面的函数是对外的函数,所以内部还会有一些同名的函数,但是参数列表不一样,实现数据的封装,外部的调用不会涉及到内部的数据对象
bool BinTree
//类外函数
BinNode
//建立树结构
void creatBinaryTree(BinTree
//读入数据,为存入树结构做准备工作
void preOrder1(BinNode
//通过前序遍历的方式,在A树中寻找B树的根节点C
bool compare(BinNode
//逐个比较取入容器中的A中C的子树与B中C的子树各个节点是否一致
2.3算法思想的设计
记输入的两个二叉树为分别为a1,a2
记a2的根节点对应的值为h
1)先创建二叉树的类来储存输入的元素
2)a1中进行遍历查找h。
3)在未查找到h,则输出‘no’并return
4)若查到h则返回以h为根节点的二叉树记做e
5)对a2和e分别进行先序遍历,并将遍历到的节点装入两个容器中,若遍历到的左节点或右节点为空则将‘#’装入容器
(若不进行插“#”的操作,不能保证两个二叉树前序遍历相同则两个二叉树相同)
6)对两个容器进行size的比较,
若不同则输出“no”并返回
若相同则对两个容器进行遍历逐个比较若有不同输出“no”并返回
直到遍历完容器中所有元素,此时说明两个容器元素相同,即两个二叉树相同,也说明a2为a1的子树,输出“yes”并return
2.4关键功能的算法步骤(不能用源码)
1.二叉树节点类与二叉树类的实现
这是本次实验的底层代码,二叉树节点类与二叉树的类,以及相关的部分成员函数,这些在实验三中有体现了,这里主要是将实验三中部分有用的代码进行迁移,并将无关的代码删除。主要是preorder前序遍历函数的改写,因为是对于该子树所有节点的一个保存,因此需要在前序遍历时将节点全部存入容器vector中,以便之后的比较。
2.在A树中寻找B树的根节点C
这是本题的关键算法,倘若不能在A树中找到B树的根节点C,那么说明一定不存在这样的一个树B作为A的子树。领悟这一点也是解答本题的关键。至于找到C之后对于两边的C的子树的储存与注意比较,就是自然而然的了。
3、对于容器中元素的逐一比较
考虑到有可能因为元素数量不同而本身就不可能是成立的,故需要在一开始就检查是否两个vector内元素个数相同,若不相同则直接退出。若相同,则用循环逐个检查每一个元素,若仍然相同,则返回答案。
4、特别注意”#”的意义
特别注意对于空节点的处理,因为对于仅有前序遍历,是没有办法唯一确定出一棵二叉树的,所以本题的特殊性在于它同时保存了每个空节点(也就是叶子节点)。若不进行插“#”的操作,不能保证两个二叉树前序遍历相同则两个二叉树相同。
3.算法性能分析
3.1时间复杂度
该算法的时间复杂度是O(n),下面是具体分析。由于大多是递归函数,我们主要采取功能的方法来分析。
1、准备部分:
creatBinaryTree();的两次调用,为0(1),但在creatBinaryTree()中又调用了creatBinaryTree
2、在A树中查找B树的根节点C:
BinNode
3、分别存储A中C的子树与B中C的子树的各个节点:
这里在函数compare中调用了两次preorder1函数,preorder1函数的功能是在前序遍历的同时以前序遍历的方式存储各个节点,这种遍历方式是O(n)的,记作c3n;
4、compare函数主体的逐个比较:
for循环逐个比较,显然为O(n),记作c4n;
综上所述,时间复杂度为
![]()
3.2空间复杂度
由于使用链表结构存储二叉树,而又不是morris算法遍历,仅仅使用递归来遍历,所以该算法的空间复杂度是O(n)
4.不足与反思
在算法上本题应该已经是比较优化的了,包括采取先判断个数是否相同等方法来剪枝,达到了很好的优化效果。但在遍历上,有一种morris算法可以将空间复杂度降到O(1),可以考虑。此外如果还有其他不足或可优化的地方,请务必向我提出。
【源代码】
BinaryTreeJudge.cpp
#include
#include"BinaryTree-realize.h"
#include"string"
#include
using namespace std;
int main()
{
BinTree* BT = new BinTree;
creatBinaryTree(BT);
BinTree* BT1 = new BinTree;
creatBinaryTree(BT1);
BinNode* tem = BT->find(BT->getRoot(), BT1->getRoot()->getValue());
if (tem!=NULL)
{
if (compare(tem, BT1->getRoot()))
{
cout << "yes";
return 0;
}
}
else cout << "no";
cout << "no";
return 0;
} BinaryTree-ADT.h
//BinaryTree-ADT.h
//二叉树ADT的定义和声明
#include
using namespace std;
template
class BinNode//结点类
{
private:
BinNode*lc;//左孩子
BinNode*rc;//右孩子
E elem;
public:
BinNode();//默认构造函数,设置左右孩子为空
BinNode(E tmp, BinNode*l=NULL, BinNode*r=NULL);//带参构造函数
BinNode*left();//返回左孩子
BinNode*right();//返回右孩子
void setLeft(BinNode*l);//设置左孩子
void setRight(BinNode*r);//设置右孩子
void setValue(E tmp);//设置当前结点的值
E getValue();//获得当前结点的值
bool isLeaf();//判断当前结点是否为叶子结点
};
template
class BinTree//二叉树类
{
private:
BinNode*root;//根结点
void clear(BinNode*r);//清空二叉树
public:
BinTree();//默认构造函数
~BinTree();//析构函数
bool BinTreeEmpty();//判断二叉树是否为空
BinNode*getRoot();//获得根节点
void setRoot(BinNode*r);//设置根节点
//下面的函数是对外的函数,所以内部还会有一些同名的函数,
//但是参数列表不一样,实现数据的封装,外部的调用不会涉及到内部的数据对象
void preOrder(void(*visit)(BinNode*node));
//先序遍历,传入相对应的访问函数即可对该当前结点实现不同功能的访问(本程序为输出)
BinNode* find(BinNode* tmp, E e);//查找二叉树中是否含有某个名为e的结点
}; BinaryTree-realize.h
//BinaryTree-realize.h
//二叉树ADT的实现
#include"BinaryTree-ADT.h"
#include
#include"string"
#include
//BinaryTreeNode二叉树的节点的实现
template
BinNode::BinNode()//默认构造函数,设置左右孩子为空
{
setLeft(NULL);
setRight(NULL);
}
template
BinNode::BinNode(E tmp, BinNode*l, BinNode*r)//带参构造函数
//模板函数的默认参数似乎必须在第一次声明的时候给出,也就是说,这里不能有两个=NULL
//详情参见https://blog.csdn.net/u013457310/article/details/89510406
{
elem=tmp;
lc=l;
rc=r;
}
template
BinNode* BinNode::left()//返回左孩子
{
return lc;
}
template
BinNode* BinNode::right()//返回右孩子
{
return rc;
}
template
void BinNode::setLeft(BinNode*l)//设置左孩子
{
lc=l;
}
template
void BinNode::setRight(BinNode*r)//设置右孩子
{
rc=r;
}
template
void BinNode::setValue(E tmp)//设置当前结点的值
{
elem=tmp;
}
template
E BinNode::getValue()//获得当前结点的值
{
return elem;
}
template
bool BinNode::isLeaf()//判断当前结点是否为叶子结点
{
return (lc==NULL && rc==NULL);
}
//BinaryTree二叉树的实现
template
BinNode* BinTree::find(BinNode* tmp, E e)
{
if (tmp == NULL)return NULL;
else if (tmp->getValue() == e)return tmp;
else
{
BinNode* tmp1 = find(tmp->left(), e);
if (tmp1)return tmp1;
else
{
BinNode* tmp2 = find(tmp->right(), e);
if (tmp2)return tmp2;
}
}
return NULL;
}
template
BinTree::BinTree()//默认构造函数
{
root=new BinNode;
}
template
BinTree::~BinTree()//析构函数
{
clear(root);
}
template
bool BinTree::BinTreeEmpty()//判断二叉树是否为空
{
if (root == NULL) return true;
else return false;
}
template
BinNode* BinTree::getRoot()//获得根节点
{
return root;
}
template
void BinTree::setRoot(BinNode*r)//设置根节点
{
root = r;
}
//下面的函数是对外的函数,所以内部还会有一些同名的函数,但是参数列表不一样,
//实现数据的封装,外部的调用不会涉及到内部的数据对象
//类外函数
template
BinNode* creatBinaryTree(string s[], int& x, int n)
{
if (s[x] == "#")
return NULL;
else
{
BinNode* node = new BinNode(s[x]);
x = x + 1;
if (x < n)
node->setLeft(creatBinaryTree(s, x, n));
x = x + 1;
if (x < n)
node->setRight(creatBinaryTree(s, x, n));
return node;
}
}
void creatBinaryTree(BinTree* BT)
{
int n = 0;
string te;
cin >> te;
n = te.size();
string* s = new string[n];
for (int i = 0; i < n; i++)
{
s[i] = te[i];
}
int now = 0;
BT->setRoot(creatBinaryTree(s, now, n));
}
template
void preOrder1(BinNode* tmp, vector< string>& ve)
{
if (tmp == NULL)
{
ve.push_back("#");
return ;
}
ve.push_back(tmp->getValue());
preOrder1(tmp->left(),ve);
preOrder1(tmp->right(),ve);
}
bool compare(BinNode* s, BinNode* s1)
{
vector ve,ve1;
preOrder1(s, ve);
preOrder1(s1, ve1);
if (ve.size() != ve1.size())return 0;
else
{
for (int i = 0; i < ve.size(); i++)
{
if (ve[i] != ve1[i])return 0;
}
}
return 1;
}