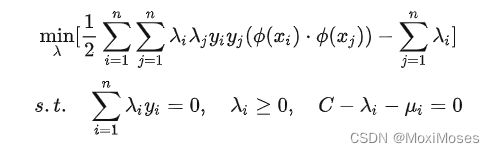2023.02.19 学习周报

---

摘要

This week, I read an article about the self-attention mechanism, this article proposes a novel method, that is, fusing item similarity models with self-attention networks for sequential recommendation, it aims to solve the following two problems, namely, the imperfect modeling of users’ global preferences in most sequential recommendation methods based on DL and the uncertainty of users’ intentions brought by candidate projects. The innovation of this article is to take the most advanced SASRec as the local representation learning module, and further propose the global representation learning module and the gating module.Finally, the research on five common datasets shows that the performance of the model is higher than the current latest baseline. In addition, I learn the mathematical knowledge related to SVM, the main content of which is the dual problem, which can be used to solve the optimization problem of SVM.

本周，我阅读了一篇关于自注意力机制相关的文章，文章提出了一种新颖的方法，即将项目相似性模型与自注意力网络融合用于顺序推荐，旨在解决以下两个问题，即大多数基于深度学习的顺序推荐方法中用户全局偏好的不完善建模和候选项目带来的用户意图的不确定性。文章的创新点在于将最先进的自我注意力顺序推荐模型（SASRec）作为本地表示学习模块，并且进一步提出了全局表示学习模块和门控模块。最后，在五个常用数据集上研究表明，模型的表现均高于当前最新的基线。此外，我学习了SVM相关的数学知识，主要内容是对偶问题，用此思想可以解决SVM优化问题。

---

文献阅读

1.题目

文献链接：FISSA: Fusing Item Similarity Models with Self-Attention Networks for Sequential Recommendation

2.摘要

Sequential recommendation has been a hot research topic because of its practicability and high accuracy by capturing the sequential information. As deep learning (DL) based methods being widely adopted to model the local and dynamic preferences beneath users’ behavior sequences, the modeling of users’ global and static preferences tends to be underestimated that usually, only some simple and crude users’ latent representations are introduced. Moreover, most existing methods hold an assumption that users’ intention can be fully captured by considering the historical behaviors, while neglect the possible uncertainty of users’ intention in reality, which may be influenced by the appearance of the candidate items to be recommended. In this paper, we thus focus on these two issues, i.e., the imperfect modeling of users’ global preferences in most DLbased sequential recommendation methods and the uncertainty of users’ intention brought by the candidate items, and propose a novel solution named fusing item similarity models with self-attention networks (FISSA) for sequential recommendation. Specifically, we treat the state-of-the-art self-attentive sequential recommendation (SASRec) model as the local representation learning module to capture the dynamic preferences beneath users’ behavior sequences in our FISSA, and further propose a global representation learning module to improve the modeling of users’ global preferences and a gating module that balances the local and global representations by taking the information of the candidate items into account. The global representation learning module can be seen as a locationbased attention layer, which is effective to fit in well with the parallelization training process of the self-attention framework. The gating module calculates the weight by modeling the relationship among the candidate item, the recently interacted item and the global preference of each user using an MLP layer. Extensive empirical studies on five commonly used datasets show that our FISSA significantly outperforms eight state-of-the-art baselines in terms of two commonly used metrics.

3.介绍

背景：推荐系统是缓解信息过载问题的智能工具，尤其是在用户意图不确定时。传统推荐系统仅处理一般推荐，其中用户-项目交互记录可以放置在二维评级矩阵中，以便通过填充该矩阵的空缺来实现预测。与一般推荐不同，顺序推荐将用户的历史记录视为项目序列而不是项目集，以便准确预测他们将与之互动的下一个项目。

FPMC由两部分组成，即将一类反馈矩阵分解的传统矩阵分解模型，以及对通过个性化马尔可夫链生成的过渡矩阵进行分解的新型MF模型。Fossil的改进模型用因子项目相似性模型（FISM）替换了FPMC的前一个组件，通过包括多个转换矩阵将后者的组件扩展到更高阶版本，并且还引入了一些个性化的加权因子平衡这些全球和本地偏好。

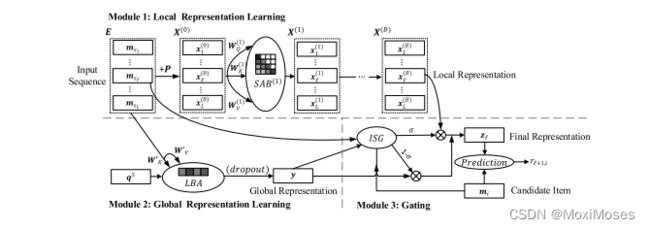
模型：FISSA不仅将有效的全局表示学习与自注意力顺序推荐（SASRec）结合起来，而且还可以平衡用户对每个候选商品的短期和长期兴趣。具体而言，模型包含三个主要组件，即本地表示学习模块，全局表示学习模块和用于平衡这两种表示的选通模块。

对于局部表示学习，作者遵循SASRec，因为它具有出色的性能以及增强动态兴趣建模；对于全局表示学习，文章应用基于位置的关注层来实现FISM的专注版本，其中引入了所有序列共享的查询向量，从而区分了生成全局变量的不同项目的重要性；文章设计了基于多层感知器的门控网络，该网络通过考虑因素来决定局部和全局表示的贡献率候选项目，最近交互的项目与目标用户的整体偏好之间的关系。

4.本文贡献

1）文章提出了一种新的模型FISSA，以解决两个问题，即在大多数基于深度学习的顺序推荐方法中，用户的全局偏好建模不完善，以及受到候选项的影响，导致用户意图的不确定性。
2）文章设计了一个全局表示学习模块，以在模型FISSA中有效地捕捉用户的全局偏好，该模块可以被看作一个基于位置的注意力层，与自注意力框架的并行化训练过程非常吻合。
3）文章在FISSA中设计了一个基于MLP的门控模块，该模块通过考虑候选项的信息来平衡本地和全局表示，从而同时处理用户意图的不确定性。
4）文章对5个常用数据集进行了广泛的实证研究，实验表明FISSA显著优于8个最先进的基线。

5.方法

5.1 Local Representation Learning

文章将局部表示学习模块建立在自注意力顺序推荐模型的基础上，该模型是一个优秀的顺序推荐模型，具有令人满意的简洁性和效率。我们将来自顶部自我注意力块的输出向量 xl(b) ∈ R1×d 作为局部表示，它代表用户行为序列中第l个步骤的动态偏好。层次结构对局部表示很重要，具体来说，底部的自关注块倾向于捕捉长期依赖关系，而较高的块可能会关注更近的依赖关系。

1）输入序列S嵌入成矩阵E = [ ms1 , , , msl ]
2）为了捕捉位置影响，加了一个Position: p = [ p1 , , , pl ]
3）最终得到了输入矩阵：X = msl + pl
4）对X进行softmax归一化得到SAL（X)
5）然后通过FFL的激活函数得到self-attention block: SAB（X）
6）SAB(X) = FFL(SAL(X)) where X ∈ Rl×d

5.2 Global Representation Learning

具有相似项目的序列往往具有相似的表示。作者认为，如果注意到更多有代表性的项目，这种效果可以得到加强。因此，文章引入一个所有序列共享的可学习查询向量qS ∈ R1×d ​来计算序列中最具代表性的项目，而不是使用平均权重的聚合。

全局表示学习模块用来提取用户的长期偏好，作者先是通过传统的推荐模型FISM来引入的。在FISM中，用户u对下一个交互物品su的偏好被建立为其他交互物品表示的聚合:

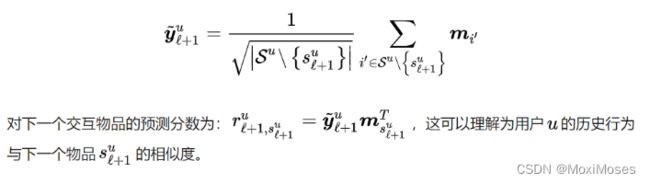
作者认为不同的历史物品应该具有不同的权重。但如何来分配权重呢？这里作者采用了attntion mechanism，但是比较有意思的是模型中的query是可学习的q∈ R1xd，通过query来实现对每个历史物品权重的分配：

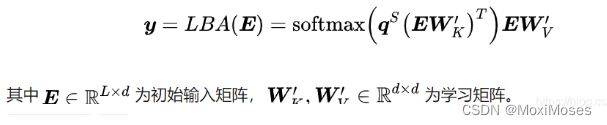
加入dropout layer：

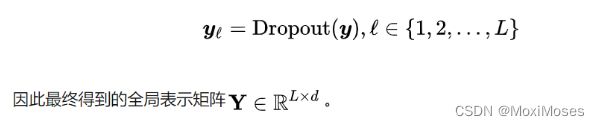
5.3 Item Similarity Gating

局部表示与全局表示的融合：如何联合局部表示和全局表示，作者早期分别做了求和和拼接的测试，结果证明求和效果更好，但作者认为这些组合方法仍然只是基于历史信息，这可能是理想化的。

为了解决序列推荐中用户意图不确定性的问题，受到神经注意物品相似度(NAIS)的启发，作者提出一个item similarity gating模块，通过建模候选物品i和最近交互的物品Sl之间的物品相似度，以及候选物品i和历史行为物品的聚合之间的物品相似度来计算局部表示和全局表示的权重：

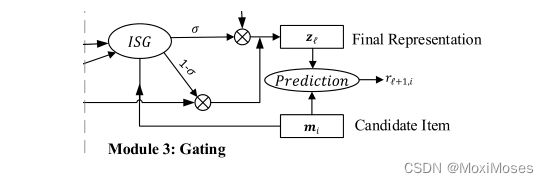
6.实验

6.1 数据集

6.2 结果

1）Performance Comparison:
如下图所示，FISSA在五个数据集上都取得了最佳性能，这清楚地表明了论文提出的模型的优越性。

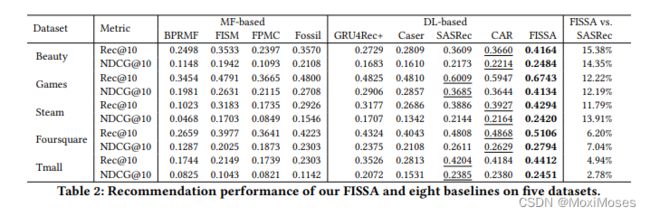
2）Ablation Study:

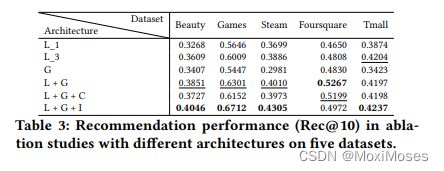
3）Quantitative Study:
如下图所示，随着维度d在Games和Steam上变大，FISSA获得了更好的结果，但在Beauty、Foursquare和Tmall上更容易过拟合，其中d=30和d=40表现最好。

如下图所示，与SASRec不同，设置区块数B=2足以让FISSA在大多数情况下获得最佳性能，而采用更多区块可能会适得其反。这是因为尽管层级结构仍然有用，但我们在FISSA中学习到的全局表示实际上是SASRec底层模块中学习到长期过渡的一种新的替代。

4）Exploratory Study:
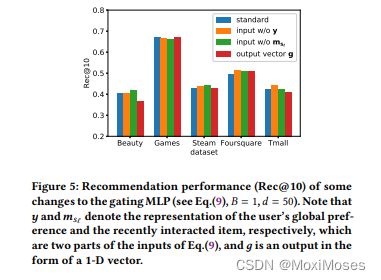
如下图所示，特征级选通在四个数据集上带来了更差的结果，尽管预计它会细化不同维度的权重。事实上，在实验中发现特征级选通会使模型更不稳定，这往往会陷入局部最优。

7.结论

文章提出了一种新颖的解决方案，即将项目相似性模型与自注意力网络融合，用于顺序推荐。具体来说，模型包括三个主要组件，即局部表示学习模块、全局表示学习模块和门控模块。文章将基于SASRec模型的局部表示学习模块，为全局表示学习设计了一个关注版本的FISM，以填补大多数基于深度学习的顺序推荐方法中对全局偏好学习考虑不足的空白。文章还设计了一个门控网络，它考虑了候选项、最近的交互和每个用户的全局偏好之间的关系，以处理用户意图的不确定性。

深度学习

运筹学-对偶问题：https://blog.csdn.net/Kobe123brant/article/details/115604380
凸优化-对偶问题：https://zhuanlan.zhihu.com/p/133457394

1.对偶问题

1.1 拉格朗日乘数法

1）等式约束优化问题

高等数学中的拉格朗日乘数法是等式约束优化问题：


上图中的方程组是等式约束的极值必要条件，但是否为极值点需根据问题本身的具体情况检验。

等式约束下的Lagrange乘数法引入了L个Lagrange乘子，我们将xi与λk看作优化变量，共有(n + L)个优化变量。

2）不等式约束优化问题

解决不等式约束优化问题的主要思想是将不等式约束条件转变为等式约束条件，引入松弛变量，将松弛变量也视为优化变量。

以下图为例：
1）加平方的原因主要是为了不再引入新的约束条件，因为要确保松弛变量大于等于0。
2）最后的方程组是不等式约束优化优化问题的KKT条件，λi称为KKT乘子。

1.2 强对偶性

对偶问题其实就是将：

转化成：

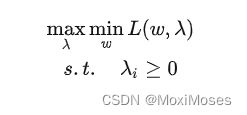
假设有一个函数f：min max f >= max min f
即最大的里面挑出最小的也要比最小的里面挑出最大的要大，这实际上就是弱对偶关系，而强对偶关系是当等号成立时，即：min max f = max min f。
如果f是凸优化问题，则强对偶性成立，而上面求出的KKT条件是强对偶性的充要条件。

2.SVM优化

SVM优化的主问题是：

求解线性可分的 SVM 的步骤为：

1）SMO（序列最小优化算法）的核心思想：每次只优化一个参数，其他参数先固定住，仅求当前这个优化参数的极值。
2）将问题转化成只变动一个参数，即仅有一个约束条件的最优化问题。
3）sign为阶跃函数：

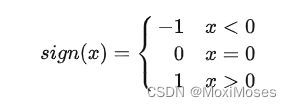
3.软间隔

3.1 解决问题

在实际应用中，完全线性可分的样本是很少的，如果遇到了不能够完全线性可分的样本，我们应该怎么办？如下图所示：

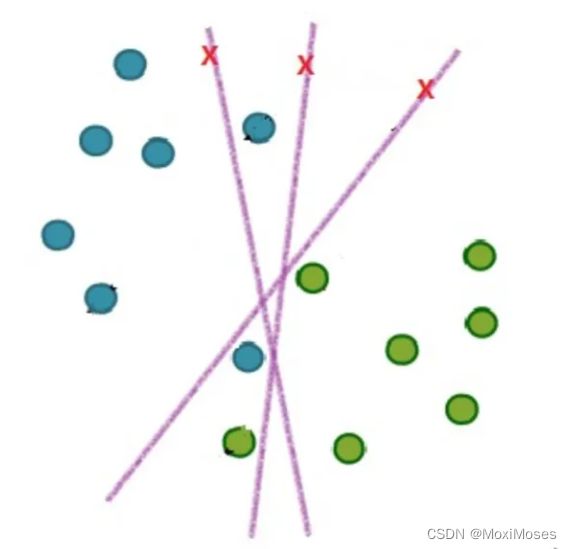
于是就有了软间隔，相比于硬间隔的严格条件，我们允许个别样本点出现在间隔带里面，比如：

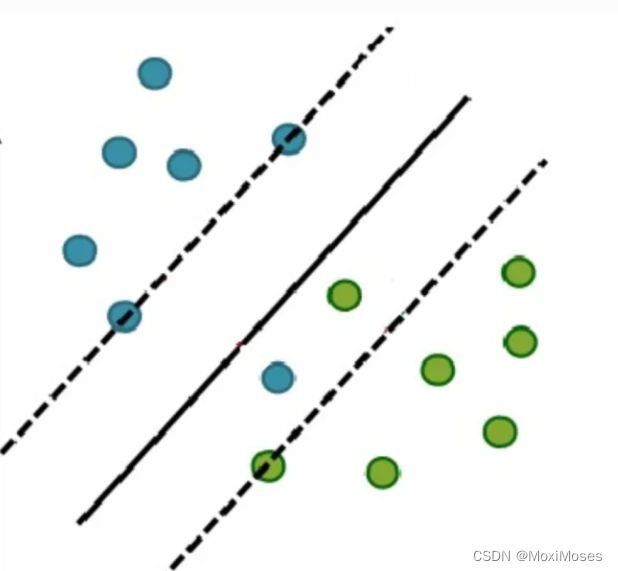
允许部分样本点不满足约束条件：

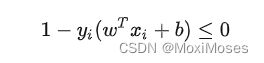
为了度量这个间隔软到何种程度，于是为每个样本引入一个松弛变量 ：

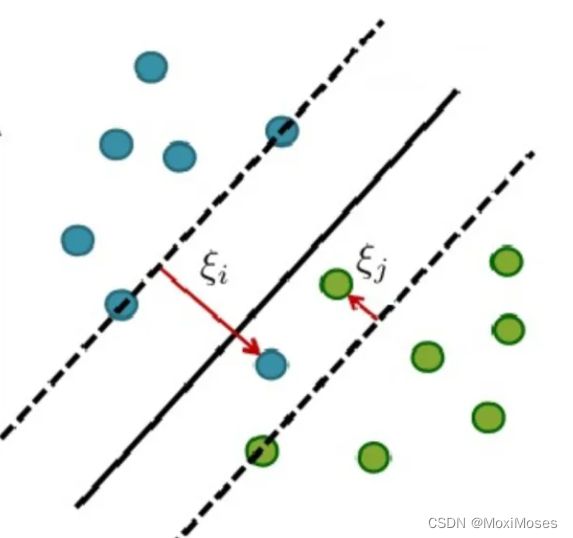
3.2 优化目标及求解

增加软间隔后优化目标变成了：

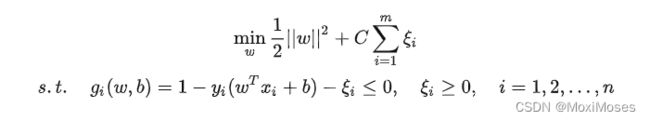
其中：C是一个大于 0 的常数，可以理解为错误样本的惩罚程度；若C为无穷大，则松弛变量必然无穷小，线性SVM就又变成了线性可分SVM；当C为有限值的时候，才会允许部分样本不遵循约束条件。

针对新的优化目标求解最优化问题：

这里有一个问题，在间隔内的样本点是不是支持向量？
从求出参数w的式子可以看出，只要是λi > 0的点都能够影响到超平面，因此都是支持向量。

4.核函数

4.1 线性不可分

实际上，我们可能会碰到的一种情况是样本点不是线性可分的，如下图所示：

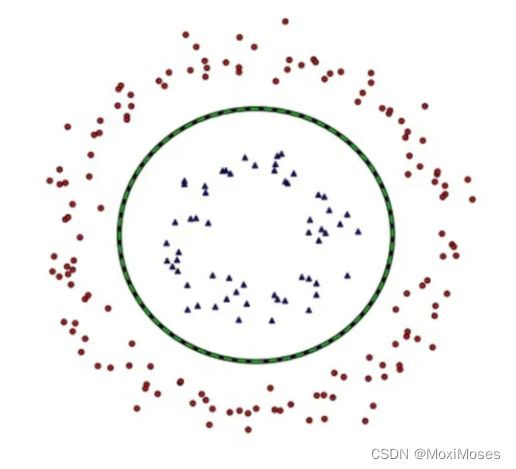
解决方法：将二维线性不可分样本映射到高维空间中，让样本点在高维空间线性可分。

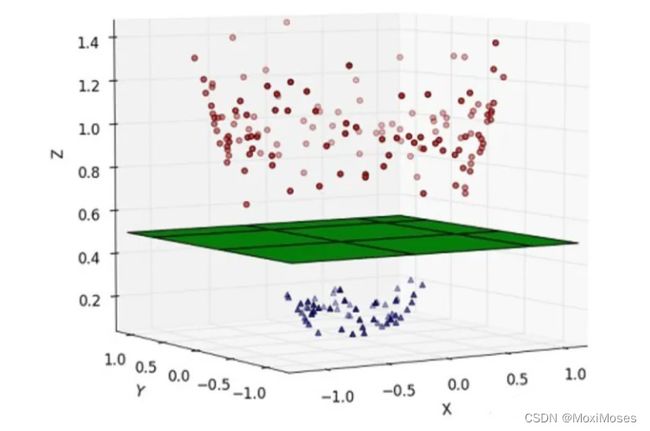
我们将 x 表示原来的样本点，用Ф(x)表示 x 映射到新的特征空间后的新向量。那么分割超平面可以表示为： f(x) = wФ(x) + b。

即非线性 SVM 的对偶问题就变成：

4.2 核函数的作用

低维空间映射到高维空间后维度可能会很大，如果将全部样本的点乘全部计算出来，计算量太大了。因此核函数的优点在于减少了我们计算量，以及减少了存储数据的内存使用量。

---

总结

本周的学习内容主要还是围绕着上周未学习完的SVM的数学知识，其中的对偶问题也是补充了自己的知识储备，收获颇丰。下周将完成对Self-attention剩余内容的学习，以及继续学习机器学习的相关知识。