py征途3之填坑(pagerank个人详解)
在开始之前请容我哭诉一下近期学业繁重,没有办法继续写博客(懒?不可能的)
py征途这个坑也是挖了许久未填的大坑,其实一直以来都有学习,甚至还做了几个小项目,这里就小宣传一波:
github的项目说明及源码
 这次的pagerank就放到csdn吧。(主要是懒,不想再去写readme)
这次的pagerank就放到csdn吧。(主要是懒,不想再去写readme)
哦,对了,我的大学课程比较拉,没有学线代和随机,下面的内容是自学的,也算是一篇小论文吧,原pdf文件和相关参考资料就放在github上了。
(不得不说,数学公示在markdown中是一生之敌,就用C代码的代码块勉强表示吧,需要的小伙伴可以下载并查看pdf哦。)
文章目录
- PageRank的算法研究
-
- 一,数学原理
-
- (一)矩阵
-
- 1 矩阵的定义
- 2 矩阵的计算
-
- (1)加法
- (2)数与矩阵相乘
- (3)矩阵与矩阵的乘法
- (4)矩阵的转置
- (二)一阶马尔可夫链
- (三)马尔可夫模型
- 二、PageRank 定义
-
- (一) 基本思想
- (二)有向图和随机游走模型
-
- 1 有向图
- 2 随机游走模型
-
- (1)定义
- (2)转移矩阵的性质
- (3)随机游走
- (三)PageRank 的基本定义
-
- 1 一阶马尔可夫链
- 2 具体定义
- 三、案例分析
-
- (一)案例描述
- (二)状态转移矩阵和初始分布向量
- (三)进行迭代运算
-
- 1 单步矩阵相乘
- 2 设计迭代相乘
- 3 非理想结果
- 四、两大常见问题和解决方法
-
- (一)常见问题
-
- 1 终止点问题
- 2 采集器陷阱问题
- (二)解决方法—— PageRank 的一般定义
- (三)案例再分析
-
- 1 单步矩阵相乘
- 五、算法设计与优化
-
- (一)初始算法设计
-
- 1 有向图和状态转移矩阵
-
- (1)需求分析
- (2)算法设计
- (3)代码设计
- (4)输出
- 2 随机游走计算 PageRank 值
- 3 预期误差达到平稳分布
-
-
- (1)需求分析
- (2)算法设计
- (3)代码设计
-
- (二)算法优化设计
-
-
- 1 优化角度
- 2 算法重设计
- 3 代码重设计
-
- (三)最终成果
-
- 1 最终代码
- 2 结果截图
- 3 总结与体会
- 参考文献
PageRank的算法研究
一,数学原理
(一)矩阵
1 矩阵的定义
由 m×n 个数 (= 1,2,…,m;j= 1,2,…,n)排成的 m 行 n 列的数表
11 12 ⋯ 1
21 22 ⋯ 2
⋮ ⋮ ⋮
1 2 ⋯
称为 m 行 n 列矩阵,简称 × 矩阵。
为表示它是一个整体,总是加一个括弧,并用大写黑体字母表示它,记作
A=(
11 12 ⋯ 1
21 22 ⋯ 2
⋮ ⋮
1 2 ⋯
)
这 × 个数称为矩阵 A 的元素,简称为元。
数位于矩阵 A 的第行 第列,称为矩阵 A 的(,)元。以数 为(,)元的矩阵可简记作()或() × , × 矩阵 A 也记作 × 。
2 矩阵的计算
(1)加法
定义:设有两个 × 阵 A=()和 B=(),那么矩阵 A 与 B 的和记作 +
规定:只有当两个矩阵是同型矩阵时,这两个矩阵才能进行加法运算
规律:矩阵加法满足下列运算规律(设 A,B,C 都是 × 矩阵):
() A +B = B +A;
()(A +B)+ C = A +(B +C)
设矩阵 A = (),记 -A = (−), -A 称为矩阵 A 的负矩阵显然有 A +(-A)= O, 由此规定矩阵的减法为 A - B = A +(- B)
(2)数与矩阵相乘
定义:数λ与矩阵 A 的乘积记作
规定:
λA=Aλ=(
11 12 ⋯ 1
21 22 ⋯ 2
⋮ ⋮
1 2 ⋯
)
规律:数乘矩阵满足下列运算规律(设 A、B 为 × 矩阵,λ、μ为数):
()(λμ)A =λ(μA)
()(λ+μ)A =λA +μA
()λ(A +B)=λA +λB
矩阵加法与数乘矩阵统称为矩阵的线性运算。
(3)矩阵与矩阵的乘法
定义:只有当第一个矩阵(左矩阵)的列数等于第二个矩阵(右矩阵)的 行数时,两个矩阵才能相乘。
设 A=()是一个 × 矩阵,B=()是一个 × 矩阵,那么规定矩阵 A 与
矩阵 B 的乘积是一个 × 矩阵 C =(),其中
= 11 + 22 + ⋯ + = ∑ ( = 1,2, … , ; = 1,2, … , )
并把此乘积记作 C = A B. 按此定义,一个 1×s 行矩阵与一个 s×1 列矩阵的乘积是一个 1 阶方阵,也就 是一个数。
由此表明乘积矩阵 A B = C 的(,)元 就是 A 的第行与 B 的第 j 列的乘积。
规律:矩阵的乘法不满足交换律,即在一般情形下,A B≠BA。对于两个 n 阶方阵 A、B,若 A B = BA,则称方阵 A 与 B 是可交换的。
矩阵的乘法虽不满足交换律,但仍满足下列结合律和分配律(假设运算都 是
可行的):
()(A B)C = A(B C)
()λ(A B)=(λA)B = A(λB)(其中λ为数)
() A(B + C)= A B +A C,(B + C)A = BA + CA
(4)矩阵的转置
定义:把矩阵 A 的行换成同序数的列 得到一个新矩阵,叫做 A 的转置矩阵,
记作 。
规律:矩阵的转置也是一种运算,满足下述运算规律(假设运算都是可行的):
()() = A
()( + )= +
() ()=
()( ) =
(二)一阶马尔可夫链
随机过程就是一些统计模型,利用这些统计模型可以对自然界的一些事物进
行预测和处理。
考虑一个随机变量的序列 X ={0,1, ⋯ , , ⋯ },这里的 表示时刻 t 的随机变量,t=0,1,2,⋯。每个随机变量(t=0,1,2,⋯)的取值集合相同,称为状态空间,表示为 S。随机变量可以是离散的,也可以是连续的。以上随机变量的序列构成随机过程(stochastic process)。
假设在时刻 0 的随机变量 X0 遵循概率分布 P(X0)= 0 ,称为初始状态分布。在某个时刻 t≥1 的随机变量 Xi 只依赖与 Xt-1,而不依赖于过去的随机变量 X={X0,X1,⋯,Xt-2} ,这一性质称为马尔可夫性,即
P(|0,1, ⋯ , −1) = P(+1|)t = 0,1,2, ⋯
具有马尔可夫性的随机序列 X={0,1, ⋯ , , ⋯ } ,称为马尔可夫链(Markov chain),或马尔可夫过程(Markov process)。条件概率分布 P(Xt|Xt-1)称为马尔可夫链的转移概率分布。转移概率分布决定了马尔可夫链的特性。
(三)马尔可夫模型
假设我们的序列状态是
⋯ −2,−1,,+1 ⋯,那么我们的在时刻 Xt+1 的状态的条件概率仅仅依赖于时刻 ,即:
P(+1| ⋯ , −2,−1,) = P(+1|)
既然某一时刻状态转移的概率只依赖于它的前一个状态,那么只要能求出
系统中任意两个状态之间的转换概率,这个马尔科夫链的模型就确定了。
二、PageRank 定义
在实际应用中许多数据都以图(graph)的形式存在,比如,互联网、社交网
络都可以看作是一个图,图数据上的机器学习具有理论与应用上的重要意义。
PageRank 算法是图的链接分析(link analysis)的代表性算法,属于图数据上的无监督学习方法。PageRank 可以定义在任意有向图上,后来被应用到社会影响力分析、文本摘要等多个问题。
(一) 基本思想
历史上,PageRank 算法作为计算互联网网页重要度的算法被提出。PageRank是定义在网页集合上的一个函数,它对每个网页给出一个正实数,表示网页的重要程度,整体构成一个向量,PageRank 值越高,网页就越重要,在互联网搜索的排序中可能就被排在前面。
假设互联网是一个有向图,在其基础上定义随机游走模型,即一阶马尔可夫
链,表示网页浏览者在互联网上随机浏览网页的过程。假设浏览者在每个网页依照连接出去的超链接以等概率跳转到下一个网页,并在网上持续不断进行这样的随机跳转,这个过程形成一阶马尔可夫链。PageRank 表示这个马尔可夫链的平稳分布。每个网页的 PageRank 值就是平稳概率。
图 1 表示一个有向图,假设是简化的互联网实例,节点 A,B,C,D 表示网页,有向边结点之间的有向边表示网页之间的超链接,边的权值表示网页之间随机跳转的概率。
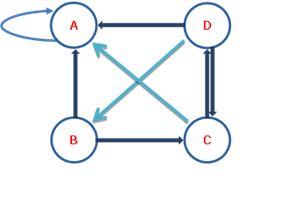
图 1
假设有一个浏览者,在网上随机游走,如果浏览者在网页 B,则下一步以 1/2的概率前往 A,1/2 的概率前往 B。
一个网页,如果指向该网页的超链接越多,随机跳转到该网页的概率也就越
高,该网页的 PageRank 值就越高,这个网页也就越重要。
一个网页,如果指向该网页的 PageRank 值越高,随机跳转到该网页的概率也就越高,该网页的 PageRank 值就越高,这个网页也就越重要。
PageRank 值依赖于网络的拓扑结构,一旦网络的拓扑(连接关系)确定,
PageRank 值就确定。
(二)有向图和随机游走模型
1 有向图
有向图(directed graph)记作 G=(V,E) ,其中 V 和 E 分别表示结点和有向边的集合。
比如,互联网就可以看作是一个有向图,每个网页是有向图的一个结点,网
页之间的每一条超链接是有向图的一条边。
强连通图:从一个结点出发到达另一个结点,所经过的边的一个序列称为一
条路径 (path) , 路径上边的个数称为路径的长度。如果一个有向图从其中任何一个结点出发可以到达其他任何一个结点,就称这个有向图是强连通图
(strongly connected graph) 。
周期性图:假设 k 是一个大于 1 的自然数,如果从有向图的一个结点出发返回到这个结点的路径的长度都是[公式]的倍数,那么称这个结点为周期性结点。
如果一个有向图不含 有周期性结点,则称这个有向图为非周期性图 (aperiodic graph),否则为周期性图。
图 2 是一个周期性有向图的例子。从结点 A 出发返回到 A,必须经过路径 AB-C-A ,所有可能的路径的长度都是 3 的倍数,所以结点 A 是周期性结点。 这个有向图是周期性图。A 是周期性结点。 这个有向图是周期性图。

图 2
2 随机游走模型
(1)定义
给定一个含有 个结点的有向图,在有向图上定义随机游走(random walk)模型,即一阶马尔可夫链,其中结点表示状态,有向边 表示状态之间的转移,假设一个结点到通过有向边相连的所有结点的转移概率相等。
具体来说,转移矩阵是一个 n 阶矩阵 M
= []×
第行 第 j 列的元素取值规则如下:如果结点 j 有条有向边连出,并且
结点是其连出的一个结点,则 = 1/;否则 = 0, , = 1,2, ⋯ ,
(2)转移矩阵的性质
≥ 0∑=1
即每个元素非负,每列元素之和为 1,即矩阵 M 为随机矩阵(stochastic matrix)。
(3)随机游走
随机游走者每经一个单位时间转移一个状态,如果当前时刻在第 j 个结点(状态),那么下一个时刻在第个结点(状态)的概率是,这一概率只依赖于当前
的状态,与过去无关,具有马尔可夫性。
根据图 1 和上述描述,可以得到每个单位时间内的转移概率表。

从而,写出该随机游走的状态转移矩阵
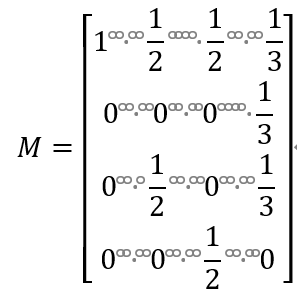
随机游走在某个时刻 t 访问各个结点的概率分布就是马尔可夫链在时刻 t 的
状态分布,可以用一个 n 维列向量 Rt 表示,那么在时刻 t+1 访问各个结点的概率分布 Rt+1 满足
+1 =
给定一个包含 n 个结点的强连通且非周期性的有向图,在其基础上定义随机
游走模型:
假设转移矩阵为 M,在时刻 0,1,2,… ,t,…访问各个结点的概率分布为
0, 0, 20, ⋯ , 0则极限lim→∞0 = 存在,极限向量 R 表示马尔可夫链的平稳分布,满足MR=R。
(三)PageRank 的基本定义
1 一阶马尔可夫链
不可约 且非周期的有限状态马尔可夫链,有唯一平稳分布存在,并且当时
间趋于无穷时状态分布收敛于 唯一的平稳分布。
根据马尔可夫链平稳分布定理,强连通且非周期的有向图上定义的随机游走
模型(马尔可夫链),在图上的随机游走当时间趋近于无穷时状态分布收敛于唯一的平稳分布。
2 具体定义
给定一个包含 n 个结点1,2, …,的强连通且非周期性的有向图在有
向图上定义随机游走模型,即一阶马尔可夫链。随机游走模型的特点是从一个结点到有向边给出的所有结点的转移概率相等,转移矩阵为 M。
这个马尔可夫链具有平稳分布 R:MR = R
平稳分布 R 称为这个有向图的 PageRank。R 的各个分量称为各个结点的
PageRank 值。
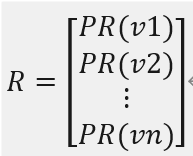
其中,(), = 1,2, ⋯ , 表示结点 vi的 PageRank 值。
那么:

M(vi)表示指向结点的结点集合。
L()表示结点连出的有向边的个数。
PageRank 的基本定义是理想化的,在这中情况下,PageRank 存在,而且可以通过不断迭代求得 PageRank 值。
三、案例分析
(一)案例描述
根据以下有向图,进行 PageRank 的数学分析和程序设计。
(二)状态转移矩阵和初始分布向量
根据随机游走模型,用户访问每个网页的可能性相同,故取初始分布向量 R0为
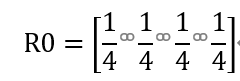
(三)进行迭代运算
设计矩阵相乘的 python 程序进行理论验证。
1 单步矩阵相乘
import numpy as np
a=np.array([[1,1/2,1/2,1/3],[0,0,0,1/3],[0,1/2,0,1/3],[0,0,1/2,0]])
b=np.array([1/4,1/4,1/4,1/4])
print(np.dot(a,b))
以转移矩阵 M 乘初始向量 R0 得
2 设计迭代相乘
import numpy as np
a=np.array([[1,1/2,1/2,1/3],[0,0,0,1/3],[0,1/2,0,1/3],[0,0,1/2,0]])
b=np.array([1/4,1/4,1/4,1/4])
while 1:
PR=np.dot(a,b)
print(PR)
b=PR
以转移矩阵 M 连乘初始向量 R0 得到向量序列:
R0 = [1 0 0 0]
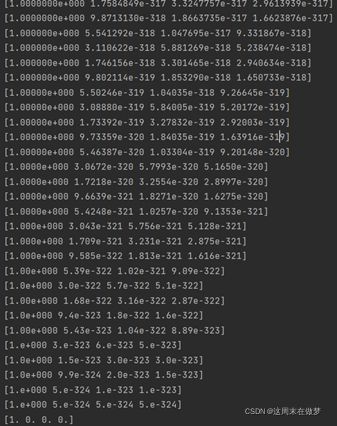
3 非理想结果
通过 R0 的最终迭代情况可以发现,PR 值陷入了一种 A 网站的权威值最高
(为 1),其他网站的权威值为 0 的情况,在这里我把它称为“采集器陷阱”。
四、两大常见问题和解决方法
实际上,案例所给模型仍旧欠缺了另一种问题的考虑,下面针对出现的问题
进行分析与修改。
(一)常见问题
1 终止点问题
问题描述:某一些网站没有出链。
修改的思路:
方法一:修改 M 矩阵;
方法二:给终止点增加一个链向其他所有外联网的连接
方法三:删除终止点
2 采集器陷阱问题
问题描述:一组网页不 链向他们之外的其他网页
修改的思路:抽税法:给每一个网页增加指向所有页面的链接,并给每个链
接一个参数(B-阻尼系数)控制的转移概率。
(二)解决方法—— PageRank 的一般定义
给定一个含有 n 个结点的任意有向图,在有向图上定义一个一般的随机游走
模型,即一阶马尔可夫链。一般的随机游走模型的转移矩阵由两部分的线性组合组成,一部分是有向图的基本转移矩阵 M,表示从一个结点到其连出的所有结点的转移概率相等,另一部分是完全随机的转移矩阵,表示从任意一个结点到任意一个结点的转移概率都是 1/n,线性组合系数为阻尼因子d(0≤d≤1)。这个一般随机游走的马尔可夫链存在平稳分布,记作 R。定义平稳分布向量 R 为这个有向图的一般 PageRank。R 由公式
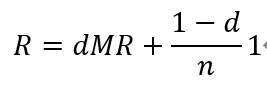
决定,其中 1 是所有分量为 1 的 n 维向量。
一般 PageRank 的定义意味着互联网浏览者,按照以下方法在网上随机游走:
在任意一个网页上,浏览者
1 要么以概率 d 决定按照超链接随机跳转,这时所有浏览者以该网页中存在
的超链接为基础,等概率从连接出去的超链接跳转到下一个网页。
2 要么以概率(1-d)决定完全随机跳转,这时以等概率 1/n 跳转到任意一个
网页。
这个机制保证从没有连接出去的超链接的网页也可以跳转出,从而解决了终
止点问题和采集器陷阱问题。这样即可以保证平稳分布,又实现了模拟真实用户的浏览情况。
一般 PageRank 的存在因此适用于任何结构的网络。
(三)案例再分析
根据以上模型,预设 d=0.85。
1 单步矩阵相乘
import numpy as np
d=0.85
a=np.array([[1,1/2,1/2,1/3],[0,0,0,1/3],[0,1/2,0,1/3],[0,0,1/2,0]])
b=np.array([1/4,1/4,1/4,1/4])
R=dnp.dot(a,b)+(1-d)/4np.ones(4)#增加以 d 为基础的完全随机概率的矩阵
print®
以转移矩阵 M 乘初始向量 R0 并增加阻尼系数得
2 设计迭代相乘
import numpy as np
d=0.85
a=np.array([[1,1/2,1/2,1/3],[0,0,0,1/3],[0,1/2,0,1/3],[0,0,1/2,0]])
b=np.array([1/4,1/4,1/4,1/4])
while 1:
R=d*np.dot(a,b)+(1-d)/4*np.ones(4)#增加以 d 为基础的完全随机概率的矩
阵
print(R)
b=R
以转移矩阵 M 连乘初始向量 R0 并增加阻尼系数得
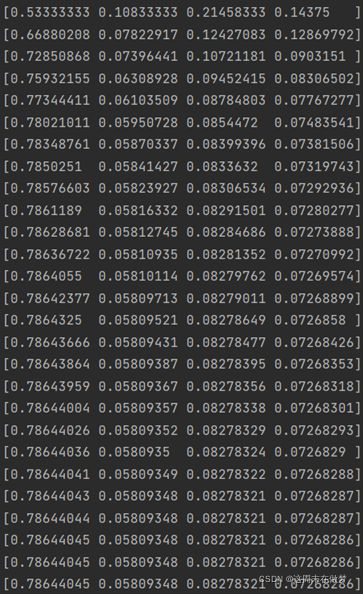
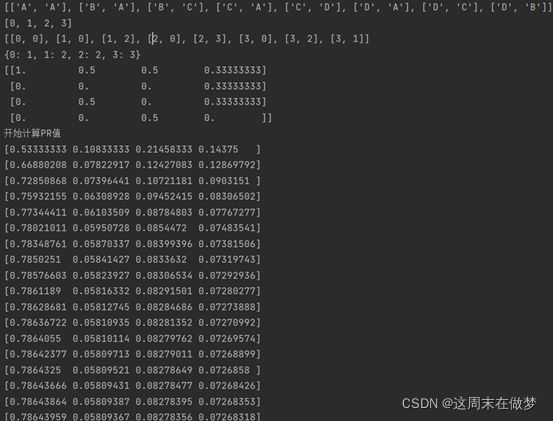
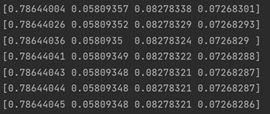
最终,PR 值稳定在[0.78644045 0.05809348 0.08278321 0.07268286]。
至此,以上终止点问题和采集器陷阱问题得到了有效的解决。
五、算法设计与优化
完成了案例分析后,PageRank 的核心模块就完成了。接下来只需要设计读入有向图的模块就可以了。
(一)初始算法设计
1 有向图和状态转移矩阵
(1)需求分析

根据案例的有向图,下面为四个网站之间的超链接关系。
根据超链接关系生成,状态转移矩阵。
(2)算法设计
读入有向图,存储边
根据边获取节点集合
获取结点的出链个数
序号转化
循环遍历初始矩阵并归一化
(3)代码设计
import numpy as np# 读入有向图,存储边
edges=[]
f = open('1.txt', 'r')
for line in f:
edges.append(line.strip('\n').split(' '))
print(edges)# 根据边获取节点的集合
nodes = []
for edge in edges:
if edge[0] not in nodes:
nodes.append(edge[0])
if edge[1] not in nodes:
nodes.append(edge[1])
print(nodes)# 获取节点出链的个数
sides=dict()
for edge in edges:
if edge[0] not in sides:
sides[edge[0]]=1
elif edge[0] in sides:
sides[edge[0]] += 1
print(sides)
#序号转化
edges_num=[]
for edge in edges:
line=[]
for i in edge:
if i=='A':
i=0
elif i=='B':
i=1
elif i=='C':
i=2
elif i=='D':
i=3
line.append(i)
edges_num.append(line)
print(edges_num)
M = np.zeros([len(nodes),len(nodes)])#生成空矩阵
#循环遍历归一化
for i in edges_num:
M[i[1],i[0]]=i[0]+1
if M[i[1],i[0]]==1:
M[i[1], i[0]]=1/sides['A']
elif M[i[1],i[0]]==2:
M[i[1], i[0]]=1/sides['B']
elif M[i[1],i[0]]==3:
M[i[1], i[0]]=1/sides['C']
elif M[i[1],i[0]]==4:
M[i[1], i[0]]=1/sides['D']
print(M)
(4)输出
2 随机游走计算 PageRank 值
使用案例中,改进后的 PageRank 算法即可。
import numpy as np
d=0.85
a=np.array([[1,1/2,1/2,1/3],[0,0,0,1/3],[0,1/2,0,1/3],[0,0,1/2,0]])
b=np.array([1/4,1/4,1/4,1/4])
while 1:
R=d*np.dot(a,b)+(1-d)/4*np.ones(4)#增加以 d 为基础的完全随机概率的矩
阵
print(R)
b=R
3 预期误差达到平稳分布
(1)需求分析
误差即精度,需要计算到什么情况下停止。按照一阶马尔可夫链的原理,最
终的迭代结果将会趋近平稳分布,那么就会出现三种情况:设置的精度迭代结束后未平稳分布;设置的精度迭代后接近平稳分布;设置的精度迭代结束前就平稳分布。
正常情况为“设置的精度迭代后接近平稳分布”。
就“设置的精度迭代结束后未平稳分布”而言,既然是设置了精度本身就是估计,即“在误差范围内”可以接受的,无需在考虑该情况。
就“设置的精度迭代结束前就平稳分布”而言,只需要在设计算法的时候予
以考虑即可。
(2)算法设计
设计误差为循环结束条件
误差为当前矩阵同下一次迭代后的矩阵差的绝对值
设置误差值为 float 的精准度即可
(3)代码设计
import numpy as np
d=0.85
a=np.array([[1,1/2,1/2,1/3],[0,0,0,1/3],[0,1/2,0,1/3],[0,0,1/2,0]])
b=np.array([1/4,1/4,1/4,1/4])
e=1
while e > 0.00000001:
R=d*np.dot(a,b)+(1-d)/4*np.ones(4)#增加以 d 为基础的完全随机概率的矩
阵
print(R)
e=R-b
e= max(map(abs, e))
b=R
(二)算法优化设计
1 优化角度
提高代码适应性:使得任意数量的网站都可以进行计算
降低代码的冗余程度:将相同的分支结构合并
2 算法重设计
序号转化重设计:使用 ASCII 转化为 DEC 数字的 chr 和 ord 函数直接映射
分支结构重设计:将“获取边结点的集合”同“获取边的数量”一同计算
3 代码重设计
import numpy as np# 读入有向图,存储边
edges=[]
f = open('1.txt', 'r')
for line in f:
edges.append(line.strip('\n').split(' '))
print(edges)
nodes = []
sides=dict()
for edge in edges:
edge[0] = ord(edge[0]) - 65
edge[1] = ord(edge[1]) - 65
# 根据边获取结点的集合
if edge[0] not in nodes:
nodes.append(edge[0])
if edge[1] not in nodes:
nodes.append(edge[1])
# 根据边获取边的字典
if edge[0] not in sides:
sides[edge[0]] = 1
elif edge[0] in sides:
sides[edge[0]] += 1
print(nodes)
print(edges)
print(sides)
M = np.zeros([len(nodes),len(nodes)])#生成空矩阵
#循环遍历归一化
for i in edges:
M[i[1],i[0]]=i[0]+1
for k in range(len(nodes)):
if M[i[1],i[0]]==k+1:
M[i[1], i[0]]=1/sides[k]
print(M)
(三)最终成果
1 最终代码
import numpy as np# 读入有向图,存储边
edges=[]
f = open('1.txt', 'r')
for line in f:
edges.append(line.strip('\n').split(' '))
print(edges)
nodes = []
sides=dict()
for edge in edges:
edge[0] = ord(edge[0]) - 65
edge[1] = ord(edge[1]) - 65
# 根据边获取结点的集合
if edge[0] not in nodes:
nodes.append(edge[0])
if edge[1] not in nodes:
nodes.append(edge[1])
# 根据边获取边的字典
if edge[0] not in sides:
sides[edge[0]] = 1
elif edge[0] in sides:
sides[edge[0]] += 1
print(nodes)
print(edges)
print(sides)
M = np.zeros([len(nodes),len(nodes)])#生成空矩阵
#循环遍历归一化
for i in edges:
M[i[1],i[0]]=i[0]+1
for k in range(len(nodes)):
if M[i[1],i[0]]==k+1:
M[i[1], i[0]]=1/sides[k]
print(M)
print("开始计算 PR 值......")
d=0.85
page_num = len(nodes)
#计算初始分布向量 R
R0 = np.ones(page_num)
for i in range(page_num):
R0[i]=1/page_num
e=1
while e > 0.00000001:
R=d*np.dot(M,R0)+(1-d)/4*np.ones(4)#增加以 d 为基础的完全随机概率的
矩阵
print(R)
e=R-R0
e= max(map(abs, e))
R0=R
2 结果截图
3 总结与体会
经历了此次的学习,不得不说兴趣的主导性是非常强悍的。从一个月前开始
对 PageRank 算法产生浓厚的兴趣开始,一直到现在自学了部分的随机过程和概率论,丝毫没有学习大学数学的压力,也许是所有的计算都可以通过程序来完成吧(偷笑)。最后,直到完成 PageRank 的全部学习和编程,我成长了许多。
每每就着清晨的黑夜开始进行程序设计的那一刻,我的内心都得到了极大的
满足,似乎我就可以掌控指尖的世界一样。程序称成了我的数学伙伴,更确切点,它让我不用在费时费力的去学习什么矩阵如何计算,不用去学什么幂法和代数算法,更不用去考虑什么逆矩阵——就简简单单的几行代码和基础数学知识就能走进数学的世界。
还记得 1 个月前发过一次说说:

那时的我恰巧听完了“网络情报收集与分析”的 PageRank 算法课程,当时
老师就比较“细致”的讲解了一下该算法。由于我既没学过线性代数,又没学过概率论,因此听矩阵相乘是懵逼的,听一阶马尔可夫链是懵逼的,听随机游走模型还是懵逼的…….心酸的往事在现在回想起来都有点好笑,明明“那么简单的知识”还好意思说“大受震撼”(微笑)——好吧,其实一切的原因都来自于知识上的不足。
知识是学不完的,唯有“学习能力”才是关键,最后,一句简单的话送给自
己——“生活很忙,那就对了。”
参考文献
[1] 郑华,孙宇锋. PageRank 思想在若干数学课程教学中的渗透[J]. 教育教学论坛, 2020,
476(30): 294-295.
[2] 同济大学数学系编. 工程数学 线性代数 第 6 版[M]. 北京:高等教育出版
社, 2014.06.
[3] 李航著. 统计学习方法 第 2 版[M]. 北京:清华大学出版社, 2019.05.
[4] 清华大学《统计学习方法》第 2 版课件
[5] 原理参考:https://blog.csdn.net/gamer_gyt/article/details/47443877
[6] 初始算法参考:https://blog.csdn.net/ten_sory/article/details/80927738
[7] PageRank 算法研究现状与展望
https://wenku.baidu.com/view/ebb4f694b9f67c1cfad6195f312b3169a451ea8d.html
[8] PageRank 算法详解:https://zhuanlan.zhihu.com/p/137561088