王道计算机组成原理课代表 - 考研计算机 第二章 数据的表示和运算 究极精华总结笔记
本篇博客是考研期间学习王道课程 传送门 的笔记,以及一整年里对
计算机组成知识点的理解的总结。希望对新一届的计算机考研人提供帮助!!!
关于对数据的表示和运算章节知识点总结的十分全面,涵括了《计算机组成原理》课程里的全部要点(本人来来回回过了三遍视频),其中还陆陆续续补充了许多内容,所以读者可以相信本篇博客对于考研计算机组成原理 “数据的表示和运算” 章节知识点的正确性与全面性;
但如果还有自主命题的学校,还需额外读者自行再观看对应学校的自主命题材料。
计算机组成原理笔记导航
- 第一章 计算机系统概述
- 第二章 数据的表示和运算
⇦当前位置- 第三章 存储系统
- 第四章 指令系统
- 第五章 中央处理器
- 第六章 总线
- 第七章 输入输出系统
计算机组成原理 复试精简笔记 (加班中...)- 408 全套初复试笔记汇总 传送门
如果本篇文章对大家起到帮助的话,跪求各位帅哥美女们,
求赞 、求收藏 、求关注!
你必考上研究生!我说的,耶稣来了也拦不住!
食用说明书:
第一遍学习王道课程时,我的笔记只有标题和截图,后来复习发现看只看图片,并不能很快的了解截图中要重点表达的知识点。
在第二遍复习中,我给每一张截图中 标记了重点,以及 每张图片上方总结了该图片 对应的知识点 以及自己的 思考 。
最后第三遍,查漏补缺。
所以 ,我把目录放在博客的前面,就是希望读者可以结合目录结构去更好的学习知识点,之后冲刺复习阶段脑海里可以浮现出该知识结构,做到对每一个知识点熟稔于心!
请读者放心!目录展示的知识点结构是十分合理的,可以放心使用该结构去记忆学习!
注意(⊙o⊙)!,每张图片上面的文字,都是该图对应的知识点总结,方便读者更快理解图片内容。
《计算机组成原理》第2章 数据的表示和运算
【考纲内容】
P38 ~
(一) 数制与编码 网课耗时:
2 h
- 进位计数制及其相互转换;
- 定点数的编码表示;
(二) 运算方法和运算电路
网课耗时:
1.5 h
- 基本运算部件:加法器,算法逻辑单元(ALU);
- 加 / 减运算:补码加/减运算器,标志位的生成;
- 乘 / 除运算 :乘/除法运算的基本原理,乘法运算和除法电路的基本结构;
(三) 整数的表示和运算
网课耗时:
1.5 h
- 无符号整数的表示和运算;
- 带符号整数的表示和运算;
(四) 浮点数的表示和运算
网课耗时:
1.5 h
- 浮点数的表示:IEEE 754标准;
- 浮点数的加/减运算;
【复习提示】
纵观近几年的真题,不难发现 unsigned、short、int、long、float、double 等在C语言中的表示、运算、溢出判断、隐式类型转换、强制类型转换、IEEE 754浮点数的表示,以及浮点数的运算,都是考研考查的重点,需要牢固掌握。
2.1 数制与编码
2.1.1 进位计数制与其相互转换
1. 进位计数法
对于
r进制来说,r 是 基数 ,ri 是第 i 位数的 位权;
2. 不同进制之间的相互转换
学了r进制,然后学各进制之间的转换,这合理吧!
(1) 任意进制 转换为 十进制(简单的一批)
以二进制举例: (11011.1)2 = (1 * 24) + (1 * 23) + (0 * 22) + (1 * 21) + (1 * 20) (按 “权” 展开法)
感兴趣可以再去了解课本里的 按基值重复相乘(除)法 本类型还可以推广到 二进制转换为r进制,方法类似。
(2) 十进制 转换为 任意进制
重点关注 十进制 转换为 二进制
① 整数十进制 转换为 二进制
举例:将十进制数123 转为 二进制数
| 重复除以2 | 得商 | 取余数 |
|---|---|---|
| 123÷2 | 61 | 1(最低位) |
| 61÷2 | 30 | 1 |
| 30÷2 | 15 | 0 |
| 15÷2 | 7 | 1 |
| 7÷2 | 3 | 1 |
| 3÷2 | 1 | 1 |
| 1÷2 | 0 | 1(最高位) |
| 答案:(123)十 = (1111011)二 |
② 小数十进制 转换为 二进制
举例:将十进制0.6875 转为 二进制
| 重复乘2 | 得小数部分 | 取整数 |
|---|---|---|
| 0.6875×2 | 0.3750 | 1(最高位) |
| 0.3750×2 | 0.7500 | 0 |
| 0.7500×2 | 0.5000 | 1 |
| 0.5000×2 | 0.0000 | 1(最低位) |
| 答案:(0.6875)十 = (0.1011)二 |
③ 补充:特殊分数 转换为 二进制
举例:
3/100 = 0.03 (分数可以转为小数)
7/16 = (111)2 × 2-4 = [0.0111]2
9/64 = (1001)2 × 2-6 = [0.001001]2
(3) 二进制 与 八、十六进制数 之间的转换
原理:23 = 8,24 = 16,故 三位二进制 正好对应 一位八进制,四位二进制 正好对应 ==一位十六进制;==反之同理。
举例:将二进制 1111000010.01101 分别转为八进制、十六进制数
具体过程看下图(十六进制和八进制差不多过程),答案:(1702.32)八, (3C2.68)十六
3. 真数 和 机器数
- 真值 :带 “+” 或 “-” 的数;如:+15、-8;
- 机器数 :把符号 “数字化” 的数;如;:0 1111、1 1000;(一定要注意符号位)
小结
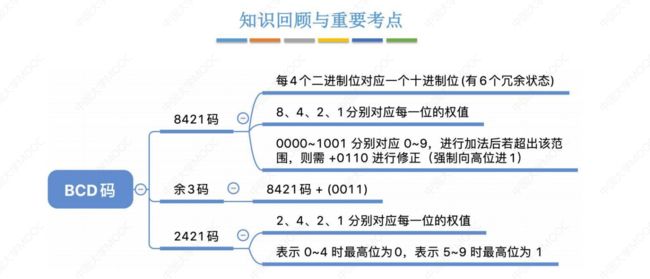
2.1.2 BCD码
BCD :Binary-Coded Decimal,用二进制编码的十进制,解决二进制转十进制的问题(快速转换、一一对应)
1. 8421BCD码
- 每四位二进制表示一位十进制(有6个冗余状态);
- 8、4、2、1分别对应每一位的权值(有权码);
- 0000 ~ 1001 分别对应 0 ~ 9,进行加法后若超出该范围,则需 +0110 进行修正;
2. 余3码
- 8421码 + (0011)2 (无权码)
3. 2421码
- 2、4、2、1分别对应每一位的权值;(有权码)
- 表示 0 ~ 4 时最高位为0,表示 5 ~ 9 时最高位为1;(避免歧义,例如5:1011 正确;0101 错误)
| 真值 | 8421BCD | 余3码 | 2421码 |
|---|---|---|---|
| 0 | 0000 | 0011 | 0000 |
| 1 | 0001 | 0100 | 0001 |
| 3 | 0011 | 0110 | 0011 |
| …… | …… | …… | …… |
| 8 | 1000 | 1011 | 1110 |
| 9 | 1001 | 1100 | 1111 |
| 10 | 0001 0000 |
小结
2.1.3 奇偶校验码
不着急学习这个,学完 2.2.1 无符号数和有符号数 再回来看这个
1. 为什么要校验码 ?
答:检测错误;
数据传输过程中可能会出现错误,校验码首先就是能发现是否数据出错,其次是纠错!
2. 码距是什么 ?
码距是指在一个编码体系中,任意两个合法码之间,对应位上编码不同的最大位数(不懂看例子)
二位二进制(此时码距为1):任意选两个(如:00、10),最多有1位不同。
三位二进制(此时码距为2):任意选两个(如:000、110),最多有2位不同。
| 东 | 南 | 西 | 北 | |
|---|---|---|---|---|
| 两位二进制 | 00 | 01 | 10 | 11 |
| 三位二进制(采用偶校验) | 0 00 | 1 01 | 1 10 | 0 11 |
3. 校验码组成
校验码 = 校验位 + 数据位
奇偶校验分为 奇校验 和 偶校验
4. 奇偶校验码原理
以 “奇校验(校验码有奇数个1)” 举例: 发送方要发送一份8位数据:01010101;
经过“奇校验”处理:1 01010101
① 如果传输过程没出错
接收方收到数据:1 01010101;
接收方“奇校验”发现没错,就将数据解包得到数据位:01010101;
② 如果数据传输过程发送1位错误(随便1位不对,数据位、校验位都可能出错)
接收方收到数据:1 11010101;
当接收方“奇校验”发现有偶数个1,这就不对了,发现错误要求重发!
③ 如果数据传输过程发送2位错误(随便2位不对)
接收方收到数据:1 10010101;
当接收方“奇校验”发现有奇数个1,就发现不出错误!!!
通过例子总结下奇偶校验码的优缺点:
优点:校验位位数少,简单,传输效率高;
缺点:只能发现奇数个错误;
2.1.4 Hamming 校验码 *
计算机网络:第三章 数据链路层 3.2 差错控制
2.1.5 CRC循环冗余校验码 *
计算机网络:第三章 数据链路层 3.2 差错控制
2.2 数据的表示
2.2.1 无符号数和有符号数
计算机中参与运算的数分为两大类:
无符号数和有符号数
1. 无符号整数
概述(先简单了解,在下面学习中理解这几句话):
计算机中的数都放在 寄存器 中,所以称寄存器的位数为 机器字长; 无符号数,就是将寄存器中的每一位数都用来存放数值;
当存放 有符号数 时,需留出位置存放符号;
当机器字长相同时,无符号数与有符号数所对应的 ==数值范围不同。==以机器字长为16位举例:
无符号数的表示范围:
0 ~ 65 535 有符号数的表示范围:
-32 768 ~ +32 767(对应补码)
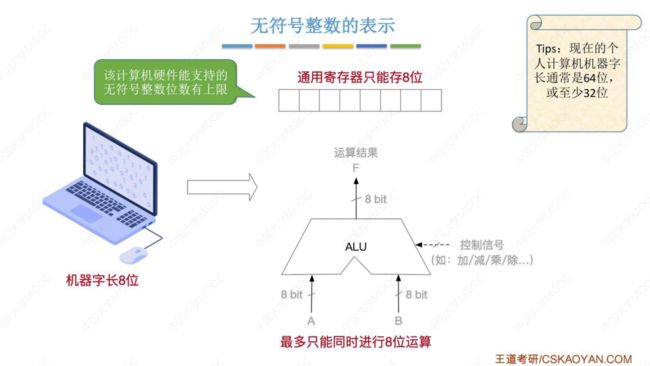
(1) 无符号整数在计算机硬件中如何表示 ?
假设现有一台计算机,通用寄存器最多能存8位
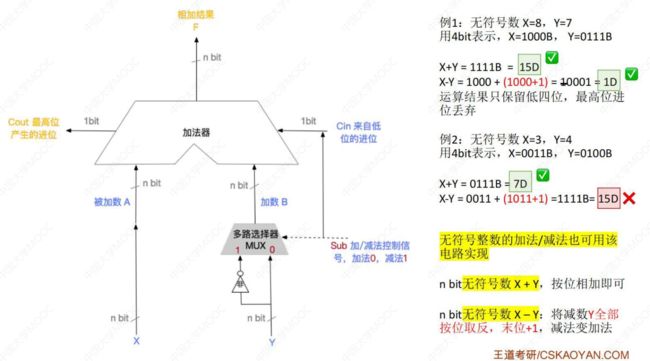
(2) 无符号整数的运算
① 无符号整数的加法运算
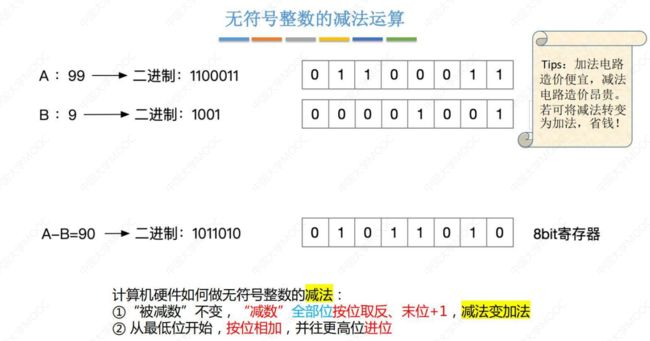
② 无符号整数的减法运算
2. 带符号数
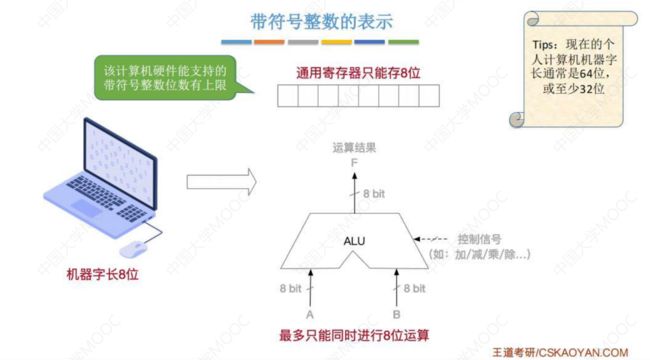
(1) 带符号整数在计算机硬件中如何表示 ?
假设现有一台计算机,通用寄存器最多能存8位
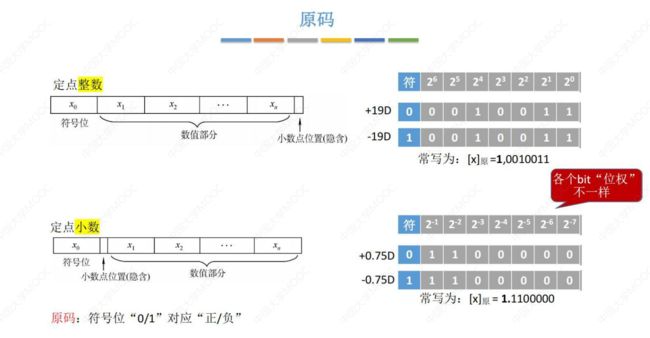
① 原码表示法
原码 :带符号的绝对表示 N位原码的表示范围:[1 1……1, 0 1……1] (符号位占1位,剩余的是数值位)
整数范围:[ -(2n-1 -1), (2n-1 -1) ]
小数范围:[-(1 - 2-(n-1)), (1 - 2-(n-1))]
真数0有两种形式: [+0]原 = 0, 000;[-0]原 = 1, 000;(注意!与补码做对比)
| 形式(举例:四位原码) | 真数(整数) | 真数(小数) | |
|---|---|---|---|
| 最大正数 | 0 111 | 7 | 0.875 |
| 最小负数 | 1 111 | -7 | -0.875 |
原码特点:简单、直观,但是 ==不适合操作数异号的加法运算,==也就是符号位不能参与运算!(补码可以)
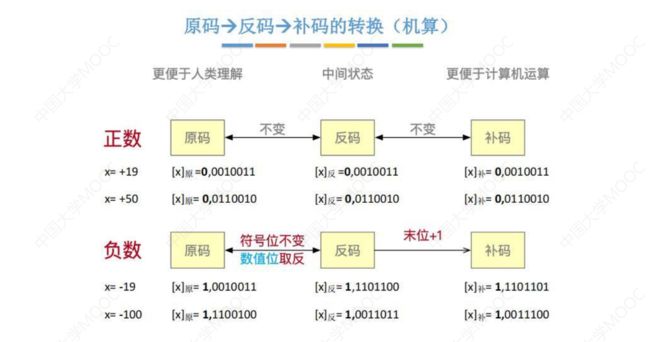
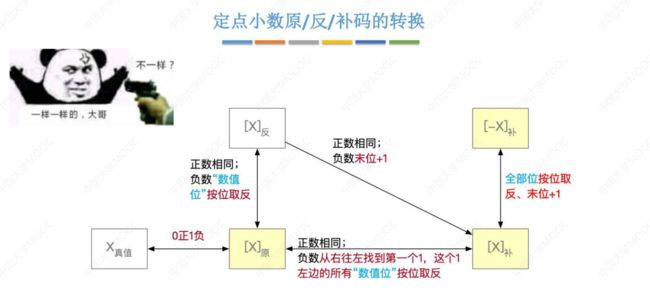
② 补码表示法
原码正数时,补码和原码相同; 原码负数时,除符号位外,各位取反,末位加1;
特点:N位补码表示范围 与 N位原码不同;补码在二进制中用来表示负数,解决 异号加法问题(符号位可以参与运算)
| -4 | -2 | -1 | 0 | 1 | 2 | 4 | |
|---|---|---|---|---|---|---|---|
| 原码 | 1 100 | 1 010 | 1 001 | 0 000 | 0 001 | 0 010 | 0 100 |
| 补码 | 1 100 | 1 110 | 1 111 | 0 000 | 0 001 | 0 010 | 0 100 |
N位补码的表示范围:[ 1 0……0, 0 1……1]
整数范围:[ -2n-1, 2n-1 - 1]
小数范围:[ -1, 1 - 2-(n-1)]
注意!与原码相比,补码的0只有一种表示形式:0000;且规定把 1000 当作 -8
| (4位补码) | 形式 | 真数(整数) | 真数(小数) |
|---|---|---|---|
| 最大正数 | 0 111 | 7 | 0.875 |
| 最小负数 | 1 000 | -8 | -1 |
③ 反码表示法
原码正数时,反码和原码相同;
原码负数时,除符号位外,各位取反;
特点:做为
原码 - 反码 - 补码互相转换的中间计算过程; N位反码的表示范围 与 N位原码相同;
(2) 带符号数的运算
例题1:补码的加法运算
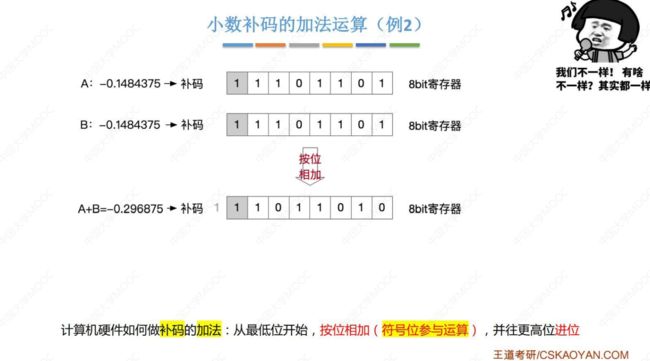
例题2:补码的加法运算
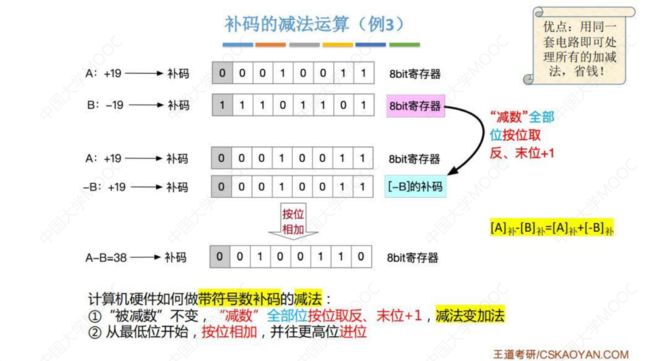
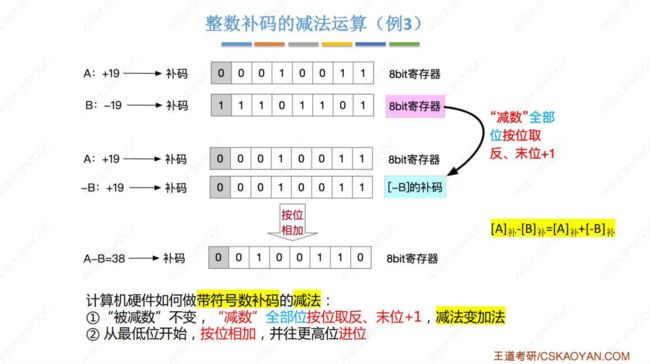
例题3:补码的减法运算
(3) 原、反、补码的特性比较
(4) 移码表示法
移码 :在补码的基础上,将符号位取反 特点:补码不能 判断数值大小,移码可以;注意!移码 只能用于表示整数!
N位移码整数的表示范围和补码相同:[ -2n-1, 2n-1 - 1];(真数0只有一种表示形式)
小结
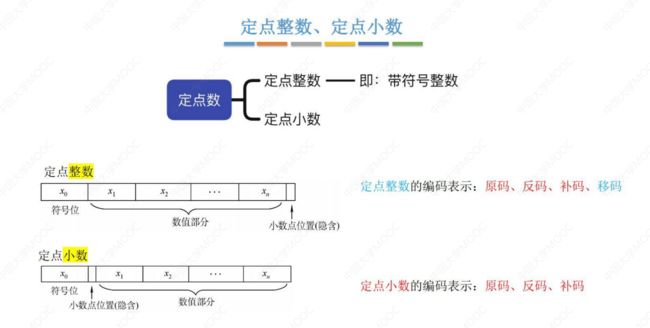
2.2.2 数的定点表示
两种方法表示小数点的存在:定点表示 和 浮点表示 ;
定点数:小数点固定在某一位置的数;
1. 定点整数 和 定点小数(纯整数 和 纯小数)
2. 数的定点表示
注意 !移码只能用来表示整数 !
2.2.3 数的浮点表示
1. 浮点数的作用
n 位的定点数 能表示的范围有限,可以采用 浮点数 可以提高数据的表示能力;
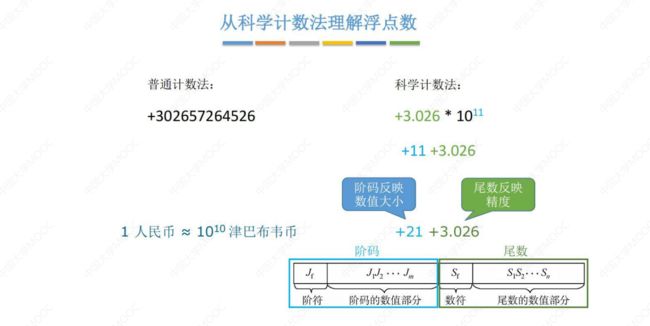
【引例】浮点数 的原理类似 科学计数法:
阶码 + 尾数;
- 阶码表示数值 大小;
- 尾数反映数值 精度;
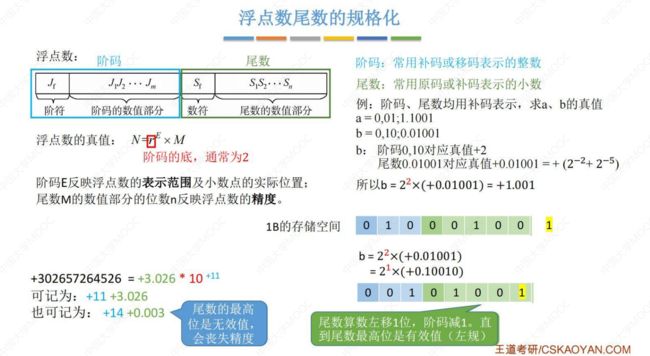
2. 浮点数的表示
浮点数的真值:N = M × r j ,由 阶码 j 和 尾数M 两部分组成。其中,M 是尾数,j 是阶码,r 是尾数的基值;
- 阶码 E 反映浮点数的 表示范围 ,是整数;
- 尾数 M 反映浮点数的 精度 ,是小数;
举例:
N = 11.0101
= 0.110101 × 210
= 1.10101 × 21
= 1101.01 × 2-10
= ……
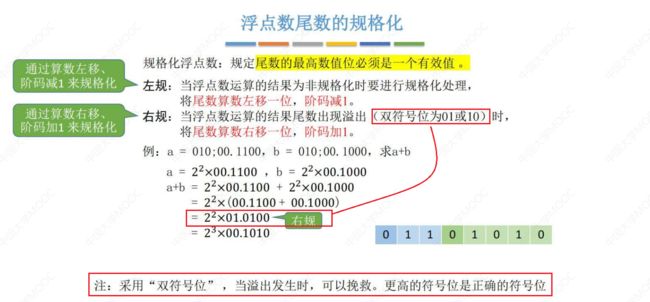
3. 规格化
图中,使用 1B = 8bit 的存储空间来存储 b,会发现它最后一位的1存储不下了;
如果把 1 舍弃,那 b 的精度就下降了,可以采用浮点数 尾数的规格化 就是来解决这样的问题;
规格化浮点数,就是要求 尾数的数值部分的第一位,必须是一个有效值 ;
| 原码表示尾数 | 补码表示尾数 | |
|---|---|---|
| 正数最大值 | 0.11 … 1 = (1 - 2-n) | 0.11 … 1 = (1 - 2-n) |
| 正数最小值 | 0.10 … 0 = 1/2 | 0.10 … 0 = 1/2 |
| 负数最大值 | 1.10 … 0 = -1/2 | 1.01 … 0 |
| 负数最小值 | 1.11 … 1 | 1.00 … 0 = -1 |
【了解】浮点数的表示范围大纲已经删除
运算结果大于最大正数时称为 正上溢,小于绝对值最大负数时称为 负上溢,正上溢和负上溢统称 上溢; 数据一旦产生上溢,计算机必须中断运算操作,进行溢出处理;
当运算结果在0至最小正数之间时称为 正下溢 ,在0至绝对值最小负数之间时称为 负下溢 ,正下溢和负下溢统称 下溢 ;
数据下溢时,浮点数值趋于零,计算机仅将其当作机器零处理;
小结
2.2.4 浮点数的标准:IEEE 754
浮点数中,阶码 一般以 移码 的形式表示,现简单回顾下移码的知识点;
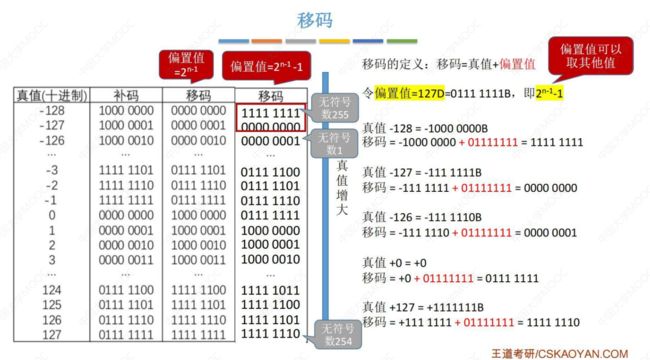
1. 移码的定义
移码最原始的定义为:
移码 = 真值 + 偏置值; 采用不同的 偏置值 ,就会得到不同的 移码;(下面例子分别采用偏置值为 128D、127D)
此时,移码的 偏置值 = 127D ,但也出现了一个问题:
例如:-128 的移码 = -1000 0000 + 0111 1111 = 1111 1111 ;
会发现 0111 1111 不够减,那么就会就其变成 1 0111 1111 ;
因为它们加减之后的结果相等于进行一个 28 的取余运算,所以加一个 1 0000 0000 给被减数,不会有影响还解决了问题;
2. IEEE 754标准
例1
例2
3. IEEE 754 的表示范围
IEEE 754所能表示的 最小绝对值 和 最大绝对值
阶码全 1,全 0 的的情况
小结
2.3 数据的运算
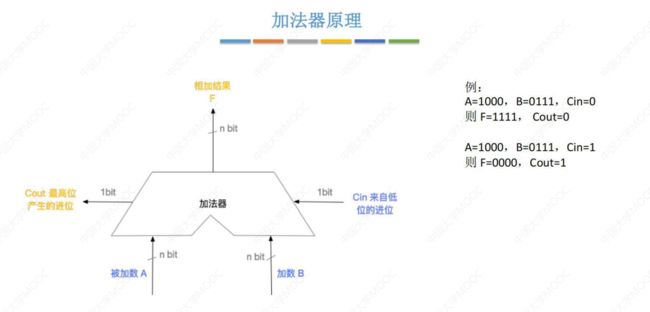
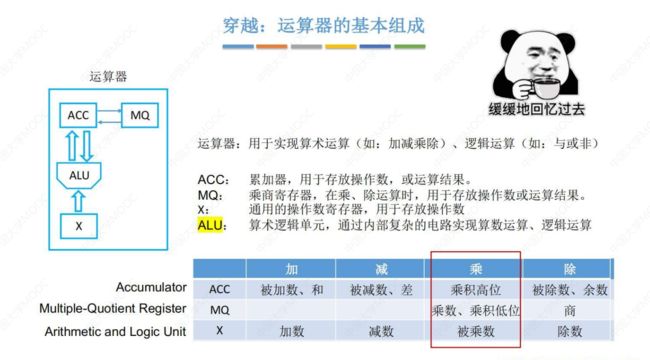
2.3.1 基本运算部件
1. ALU的作用、原理
左下侧红框是简易的 ALU 结构,两个输入信号 + 控制信号 = 输出信号 ;
右下侧是经典的 74181芯片,其中:
- ( M,S0,S1,S2,S3) ,是控制信号,M=1为逻辑运算,M=0为算术运算。S0 - S3,4bit 可以表示16种运算;
- A端和B端,分别是 4bit 的输入端;
- F端,4bit 的输出端;
- 其它未提及的端口,暂时不需要了解;
机器字长,指计算机能同时处理 nbit 运算,实际硬件原理就是 ALU 输入端的位数(例如下图中的 4bit);
为了硬件之间的协调,寄存器 也会对应 ALU 相同的位数;
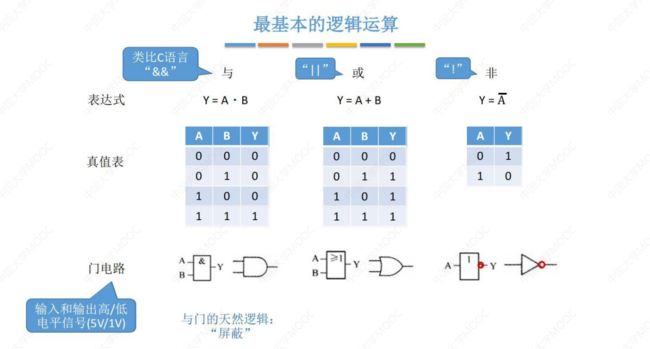
2. 电路基础知识
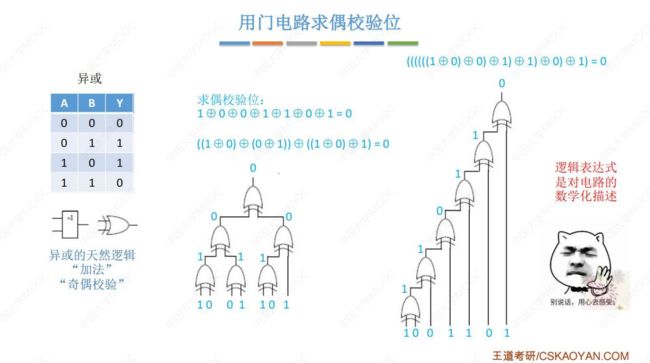
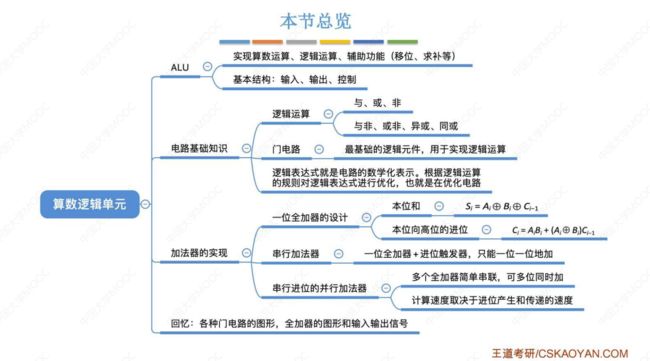
3. 加法器的实现
① 一位全加器
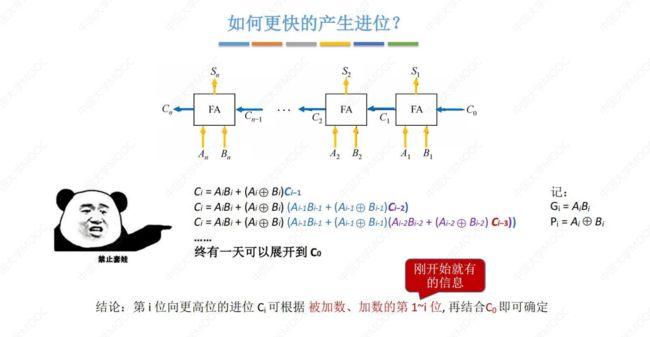
② 串行加法器
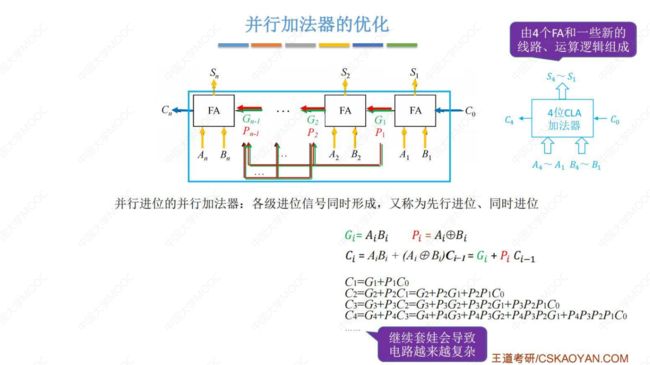
③ 并行加法器
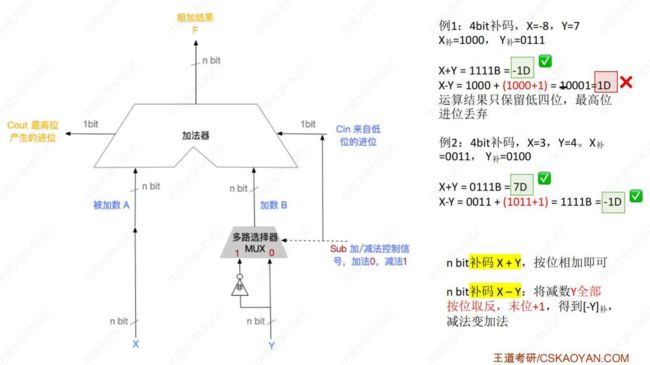
④ 补码加法器
小结
2.3.2 定点数的移位运算
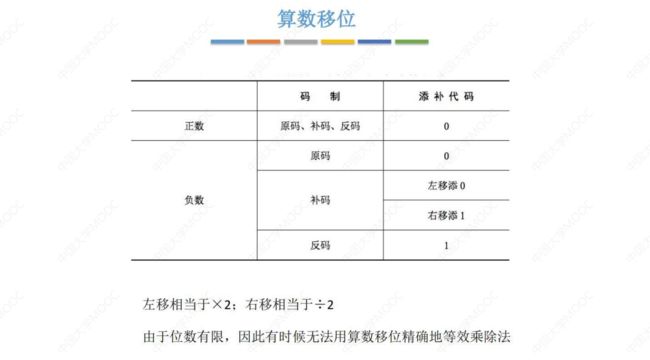
1. 算数移位
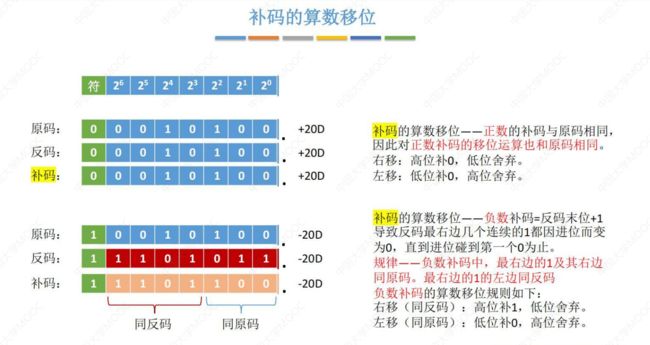
① 原码的算数移位
② 反码的算数移位
③ 补码的算数移位
2. 逻辑移位
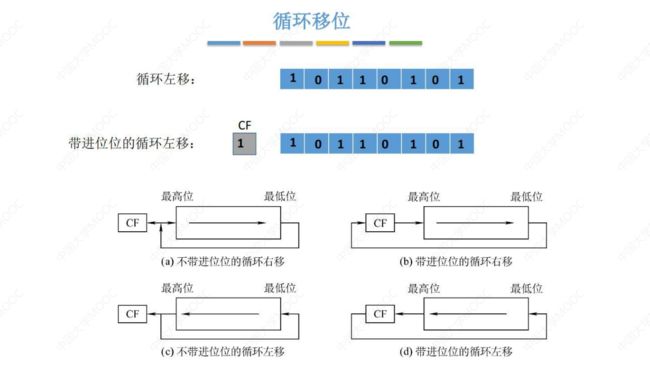
3. 循环移位
小结
2.3.3 定点数的加减运算
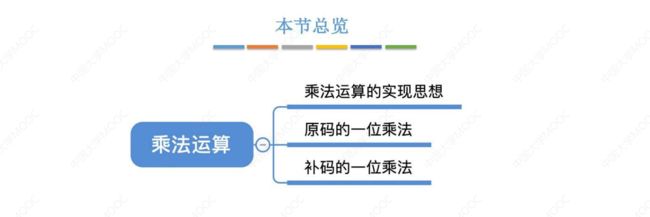
2.3.4 定点数的乘除运算
1. 定点数的乘法运算
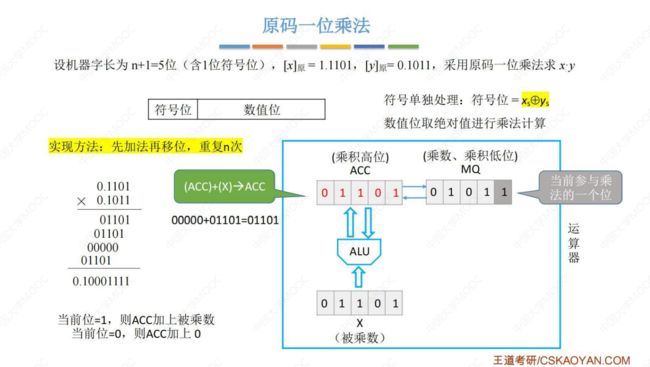
(1) 乘法运算的实现思想
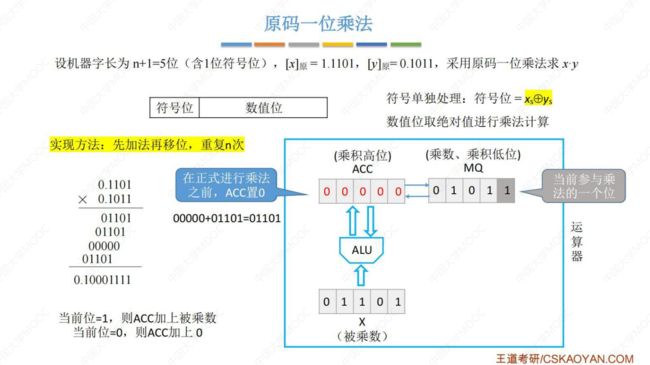
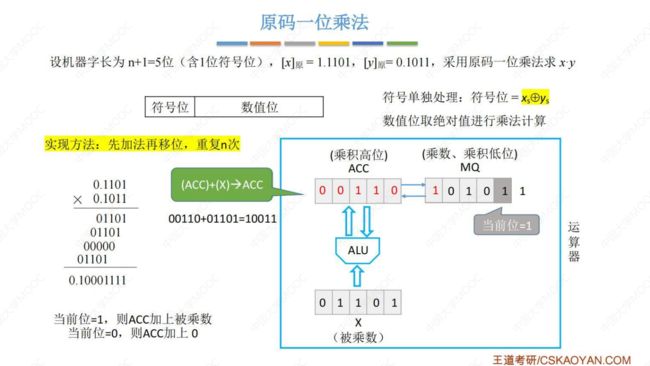
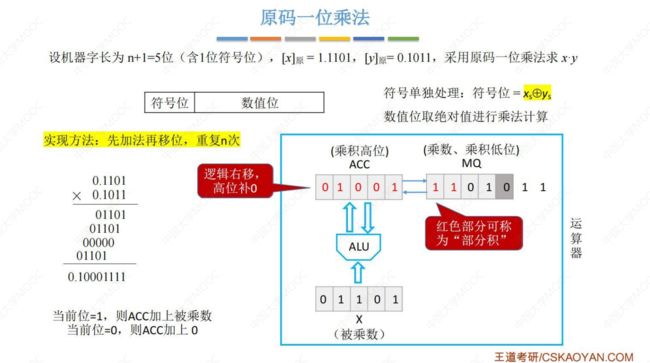
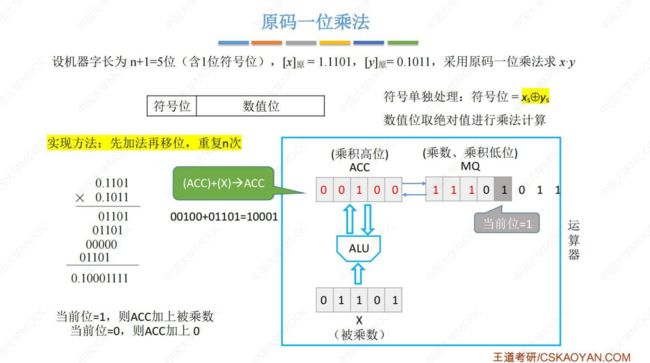
(2) 原码一位乘法
(3) 补码乘法运算
小结
2. 定点数的除法运算
(1) 除法运算的思想
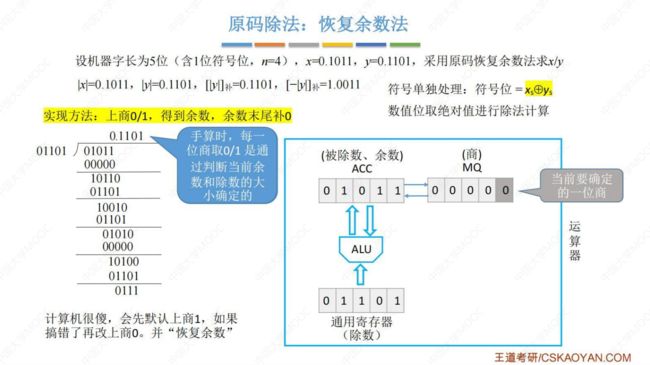
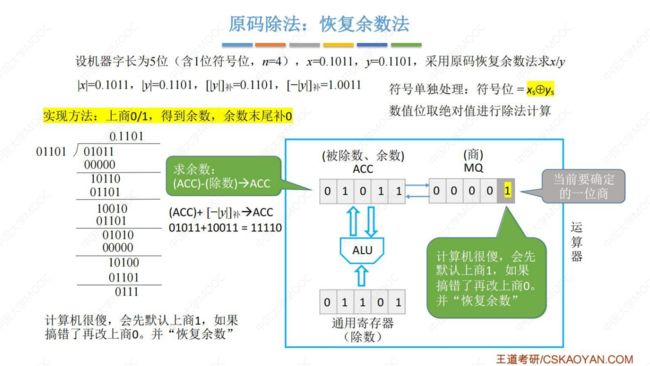
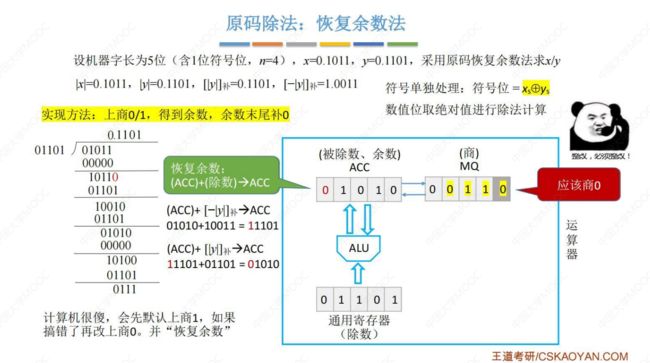
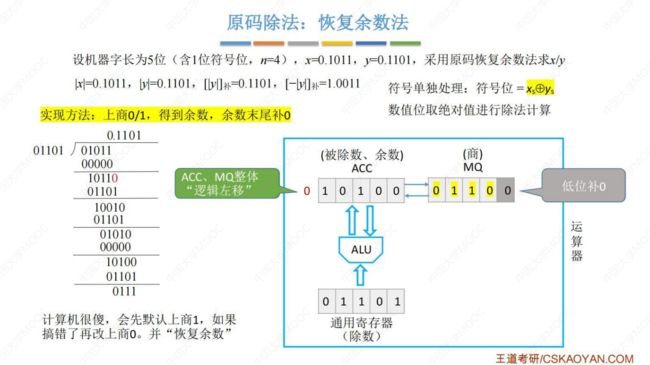
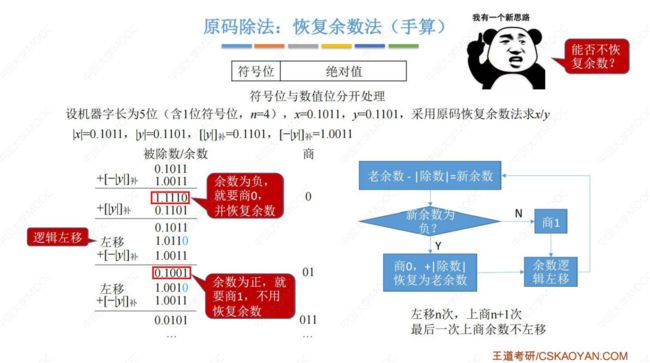
(2) 原码除法:恢复余数法
(3) 原码除法:加减交替法
(4) 补码除法:加减交替法
小结
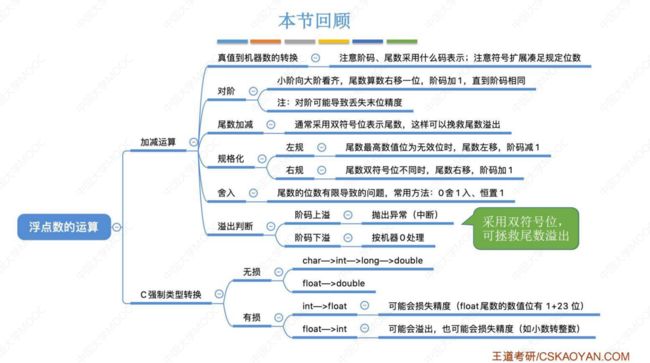
2.3.5 浮点数的加减运算
1. 加减运算步骤介绍
- ① 对阶,规定小阶往大阶靠齐;
- ② 尾数加减;
- ③ 规格化
- ④ 舍入(看具体的舍入规则);
- ⑤ 判溢出;
举例
2. 强制类型转换
下图结束了C语言中的 定点整数 如何进行强制类型转换;
小结
2.2.6 数据的存储和排序
边界对齐,是一种 空间换时间 的存储方式
2.4 常见问题和易混淆知识点
1. 如何表示一个数值数据 ?计算机中的数值数据都是二进制数吗 ?
在计算机内部,数值数据的表示方法有以下两大类:
① 直接用二进制数表示。
分为有符号数和无符号数,有符号数又分为定点数表示和浮点数表示。无符号数用来表示无符号整数(如地址等信息)。
② 二进制编码的十进制数,一般采用BCD码表示,用来表示整数。
所以,计算机中的数值数据虽然都用二进制表示,但不全是二进制,也有用十进制表示的。
后面一章有关指令类型的内容中,就分别有二进制加法指令和十进制加法指令。
2. 什么称为无符号整数的“溢出” ?
对于无符号定点整数来说,若寄存器位数不够,则计算机运算过程中一般保留低n位,舍弃高位。
这样,会产生以下两种结果:
① 保留的低n位数不能正确表示运算结果。
在这种情况下,意味着运算的结果超出了计算机所能表达的范围,有效数值进到了第n+1位,称此时发生了“溢出”现象。
② 保留的低n位数能正确表达计算结果,即高位的舍去并不影响其运算结果。
3. 如何判断一个浮点数是否是规格化数 ?
为了使浮点数能尽量多地表示有效位数,一般要求运算结果用规格化数形式表示。
规格化浮点数的尾数小数点后的第一位一定是个非零数。
因此,对于原码编码的尾数来说,只要看尾数的第一位是否为1就行;
对于补码表示的尾数,只要看符号位和尾数最高位是否相反。
需要注意的是,IEEE 754标准的浮点数尾数是用原码编码的。
4. 对于位数相同的定点数和浮点数,可表示的浮点数个数比定点数个数多吗 ?
不是,可表示的数据个数取决于编码所采用的位数。
编码位数一定,编码出来的数据个数就是一定的。
n位编码只能表示2n个数,所以对于相同位数的定点数和浮点数来说,可表示的数据个数应该一样多(有时可能由于一个值有两个或多个编码对应,编码个数会有少量差异)。
5. 浮点数如何进行舍入 ?
舍入方法选择的原则是:
① 尽量使误差范围对称,使得平均误差为0,即有舍有入,以防误差积累。
② 方法要简单,以加快速度。IEEE 754有以下4种舍入方式:
- 就近舍入:舍入为最近可表示的数,若结果值正好落在两个可表示数的中间,则一般选择舍入结果为偶数。
- 正向舍入:朝+∞方向舍入,即取右边的那个数。
- 负向舍入:朝-oo方向舍入,即取左边的那个数。
- 截去:朝0方向舍入,即取绝对值较小的那个数。
6. 现代计算机中是否要考虑原码加减运算 ?如何实现 ?
因为现代计算机中浮点数采用IEEE 754标准,所以在进行两个浮点数的加减运算时,必须考虑原码的加减运算,因为IEEE 754规足浮点数的尾数都用原码表示。
原码的加减运算可以有以下两种实现方式:
- 转换为补码后,用补码加减法实现,结果再转换为原码。
- 直接用原码进行加减运算,符号和数值部分分开进行(具体过程见原码加减运算部分)。
1)在计算机中,为什么要采用二进制来表示数据 ?
答案已在本章开头说明;
2)计算机在字长足够的情况下 能够精确地表示每个数吗 ?若不能,请举例说明。
计算机采用二进制来表示数据,在字长足够时,可以表示任何-一-个整数。而二进制表示小数时只能够用1/(2")的和的任意组合表示,即使字长很长,也不可能精确表示出所有小数,只能无限接近。例如0.1就无法用二进制精确地表示。
3)字长相同的情况下,浮点数和定点数的 表示范围与精度有什么区别 ?
字长相同时,浮点数取字长的一部分作为阶码,所以表示范围比定点数要大,而取一部分作为阶码也就代表着尾数部位的有效位数减少,而定点数字长的全部位都用来表示数值本身,精度要比同字长的浮点数更大。
4)用移码表示浮点数的阶码有什么好处 ?
浮点数进行加减运算时要比较阶码的大小,移码比较大小更方便。
检验移码的特殊值(О和max)时比较容易。阶码以移码编码时的特殊值如下。0:表示
指数为负无穷大,相当于分数分母无穷大,整个数无穷接近0,在尾数也为О时可用来表示0:尾数不为零表示未正规化的数。max:表示指数正无穷大,若尾数为0,则表示浮点数超出表示范围(正负无穷大);尾数不为0,则表示浮点数运算错误。。