王道数据结构课代表 - 考研数据结构 第五章 树和二叉树 究极精华总结笔记
本篇博客是考研期间学习王道课程 传送门 的笔记,以及一整年里对数据结构知识点的理解的总结。希望对新一届的计算机考研人提供帮助!!!
关于对树和二叉树章节知识点总结的十分全面,涵括了《王道数据结构》课程里的全部要点(本人来来回回过了三遍视频),其中还陆陆续续补充了许多内容,所以读者可以相信本篇博客对于考研数据结构“树和二叉树”章节知识点的正确性与全面性;
但如果还有自主命题的学校,还需额外读者自行再观看对应学校的自主命题材料。
数据结构与算法笔记导航
- 第一章 绪论
(无)- 第二章 线性表
- 第三章 栈和队列
- 第四章 串-KMP(看毛片算法)
- 第五章 树和二叉树
⇦当前位置- 第六章 图
- 第七章 查找(B树、散列表)
- 第八章 排序 (内部排序:八大排序动图演示与实现 + 外部排序)
数据结构与算法 复试精简笔记 (未完成)- 408 全套初复试笔记汇总 传送门
如果本篇文章对大家起到帮助的话,跪求各位帅哥美女们,
求赞 、求收藏 、求关注!
你必考上研究生!我说的,耶稣来了也拦不住!
精准控时:
如果不实际操作代码,只是粗略过一下知识点,需花费 95 分钟左右过一遍
这个95分钟是我在后期冲刺复习多次尝试的时间,可以让我很好的在后期时间紧张的阶段下,合理分配复习时间;
但是刚开始看这份博客的读者也许会因为知识点陌生、笔记结构不太了解,花费许多时间,这都是正常的。
重点!!!学习一定要多总结多复习!重复、重复、再重复!!!
食用说明书:
第一遍学习王道课程时,我的笔记只有标题和截图,后来复习发现看只看图片,并不能很快的了解截图中要重点表达的知识点。
所以再第二遍复习中,我给每一张截图中标记了重点,以及每张图片上方总结了该图片对应的知识点以及自己的思考。
最后第三遍,查漏补缺。
所以 ,我把目录放在博客的前面,就是希望读者可以结合目录结构去更好的学习知识点,之后冲刺复习阶段脑海里可以浮现出该知识结构,做到对每一个知识点熟稔于心!
请读者放心!目录展示的知识点结构是十分合理的,可以放心使用该结构去记忆学习!
注意(⊙o⊙)!,每张图片上面的文字,都是该图对应的知识点总结,方便读者更快理解图片内容。
第5章 树和二叉树
文章目录
- 第5章 树和二叉树
-
- 5.1 树和二叉树的定义
-
- 5.1.1 树的定义
- 5.1.2 树的基本术语
- 5.1.3 树的性质
- 5.1.4 二叉树的定义
- 5.2 二叉树的性质和存储结构
-
- 5.2.1 几种特殊的二叉树
-
- 1.满二叉树
- 2.完全二叉树
- 3.二叉排序树
- 4.平衡二叉树
- 5.小结
- 5.2.2 二叉树的性质
-
- 1.二叉树的参考性质
- 2.完全二叉树的参考性质
- 3.小结
- 5.2.3 二叉树的存储结构
-
- 1.顺序存储
-
- 1)算法思想
- 2)代码实现
- 3)算法分析
- 2.链式存储
-
- 1)算法思想
- 2)代码实现
- 3)小结
- 5.3 遍历二叉树和线索二叉树
-
- 5.3.1 遍历二叉树
-
- 1.算法思想
- 2.代码实现 - 先中后
- 3.先序遍历
- 4.中序遍历
- 5.后序遍历
- 6.树的深度
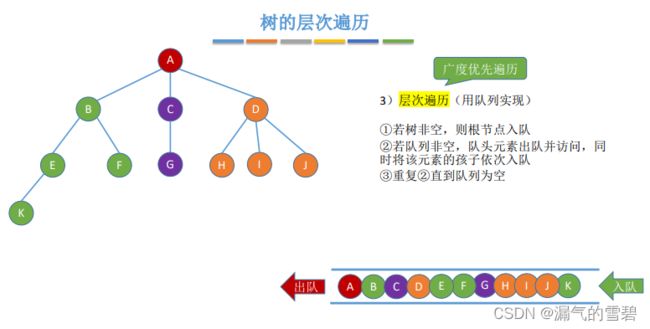
- 7.层次遍历
-
- 1)算法思想
- 2)代码实现
- 8.小结
- 5.3.2 根据遍历序列确定二叉树
-
- 1.单个遍历序列确定二叉树
- 2.算法思想 - 举例
- 3.小结
- 5.3.3 线索二叉树
-
- 1.前言
- 2.线索二叉树的基本概念
- 3.线索二叉树的存储结构
- 4.线索二叉树的构造
- 5.3.4 二叉树线索化
-
- 1.老办法
- 2.中序线索化
-
- 1)算法思想
- 2)代码实现
- 3)算法分析
- 3.先序线索化
- 4.后序线索化
- 5.小结
- 5.3.5 线索二叉树的使用
-
- 1.中序线索二叉树
-
- 1)找中序后继
- 2)找中序前驱
- 2.先序线索二叉树
-
- 1)找先序后继
- 2)找先序前驱
- 3.后序线索二叉树
-
- 1)找后序后继
- 2)找后序前驱
- 4.小结
- 5.4 树和森林
-
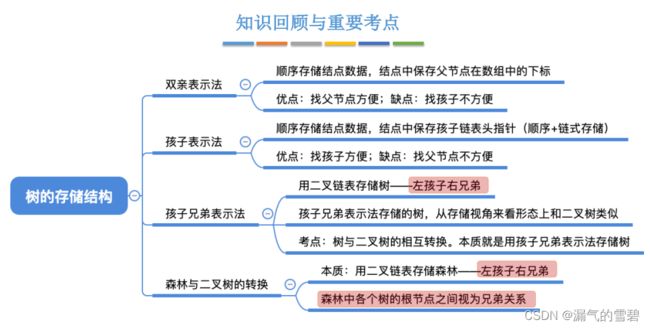
- 5.4.1 树的存储结构
-
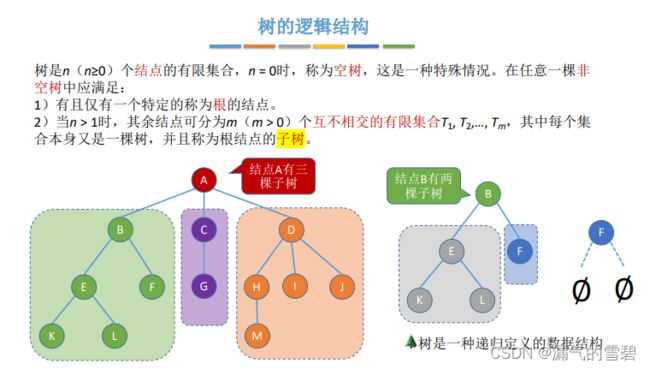
- 1.树的逻辑结构回顾
- 2.双亲表示法 - 顺序
-
- 1)算法思想
- 2)增、删操作
- 3.孩子表示法 - 顺序 + 链式
- 4.孩子兄弟表示法
- 5.树、森林与二叉树的转换
- 6.小结
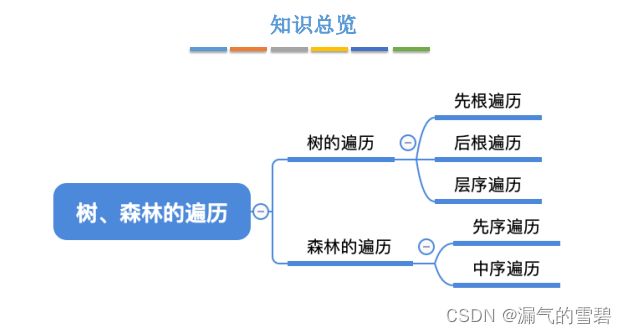
- 5.4.2 树和森林的遍历
-
- 1.树的遍历
-
- 1)先根遍历
- 2)后跟遍历
- 3)层次遍历
- 2.森林的遍历
-
- 1)先序遍历
- 2)中序遍历
- 3.小结
- 5.5 树和二叉树的应用
-
- 5.5.1 二叉排序树(BST)
-
- 1.定义
- 2.查找
- 3.插入
- 4.构造
- 5.删除
- 6.查找效率分析
- 7.小结
- 5.5.2 平衡二叉树(AVL)
-
- 1.定义
- 2.插入
- 3.调整最小不平衡子树A
-
- 1)LL
- 2)RR
- 3)LR
- 4)RL
- 5)小小小结
- 6)扩展
- 7)练习
- 4.平衡二叉树的查找
- 5.小结
- 5.5.3 哈夫曼树
-
- 1.带权路径长度
- 2.定义
- 3.构造
- 4.举例
- 5.小结
5.1 树和二叉树的定义
5.1.1 树的定义
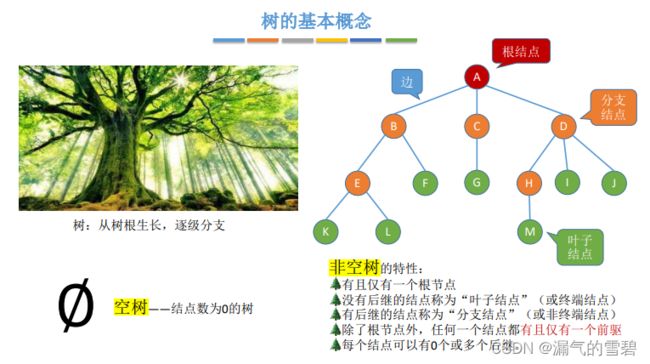
- 根节点、分支结点、边、叶子结点
- 空树、非空树
- 前驱(除根结点之外,所有结点有且只有一个前驱)、后继(0个或多个后继)
- 根(特定、唯一)
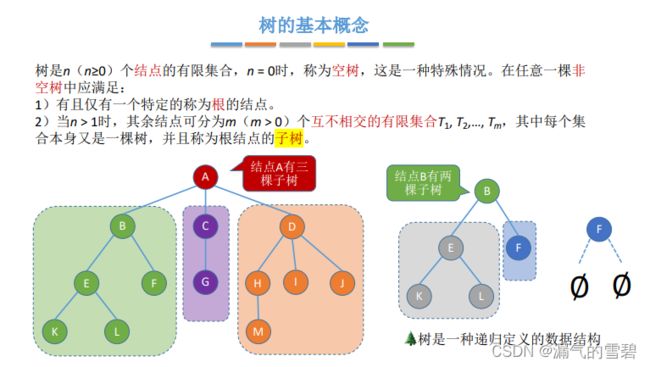
- m个不相交的有限集合
5.1.2 树的基本术语
- 祖先结点:直系长辈 - 父亲、爷爷
- 子孙结点:直系子孙
- 孩子结点:只是下一代孩子
- 兄弟结点:父亲、二叔
- 堂兄弟结点:L、M(也可以知道L、M位于同一层)
- !!! 路径:只能从上往下
- 路径长度:经过几条边
- !!!树的路径长度:从根节点到每个结点的路径长度的总和
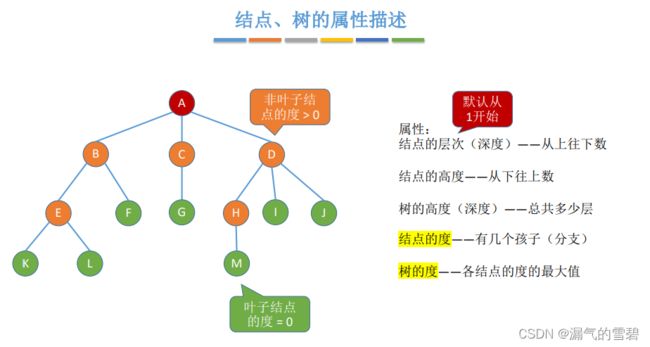
- 结点的层次:从1开始(考试的时候看实际情况),从上往下
- 结点的高度:从下往上
- 树的高度(深度):有几层
- 结点的度(和 “高度” 做区别):有几个分支
- 树的度:最大的结点度
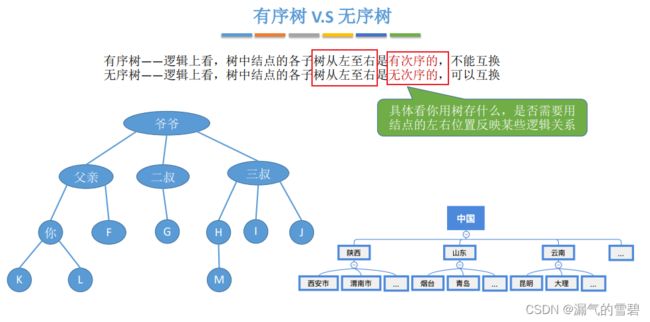
- 有序树:从左至右有次序
- 无序树
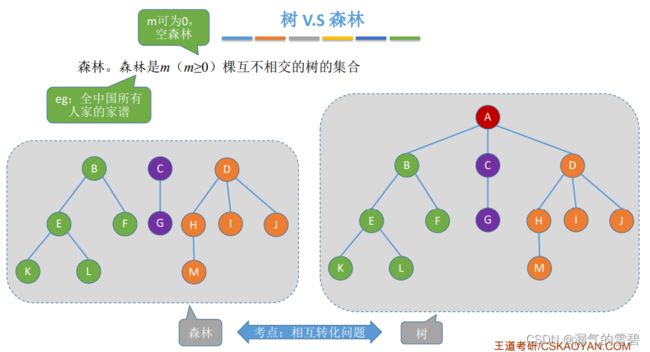
- 森林:互不相交的的树的集合
- 可以有空森林
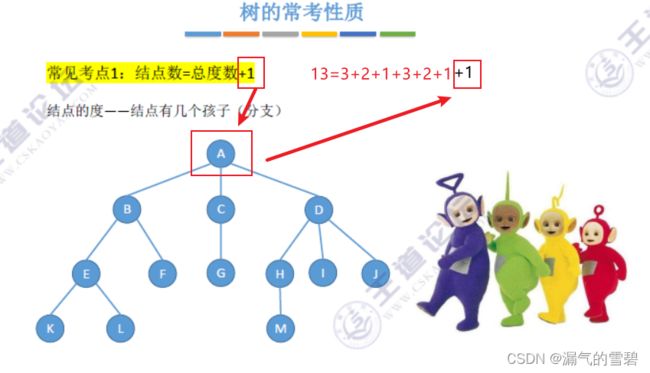
5.1.3 树的性质
- 结点数 = 总度数(边数) + 1
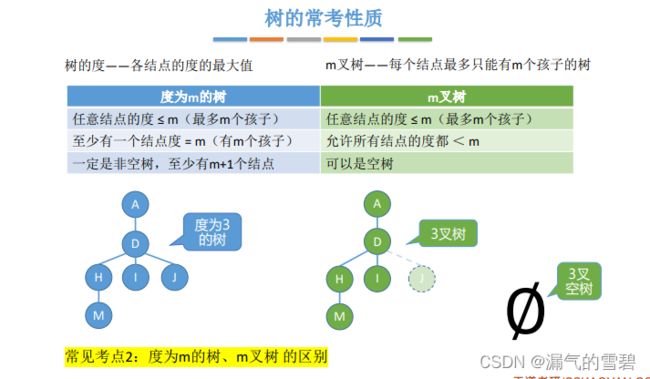
- m叉树:可以所有结点的度都 < =m(结点的度最大为m,可以为空树)
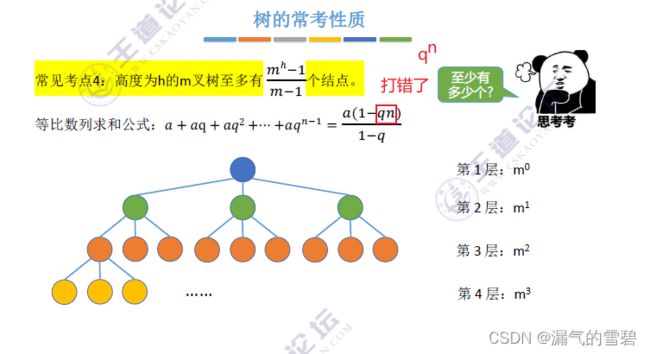
- 度为m的树:至少一个结点的度 = m(至少m+1个结点)
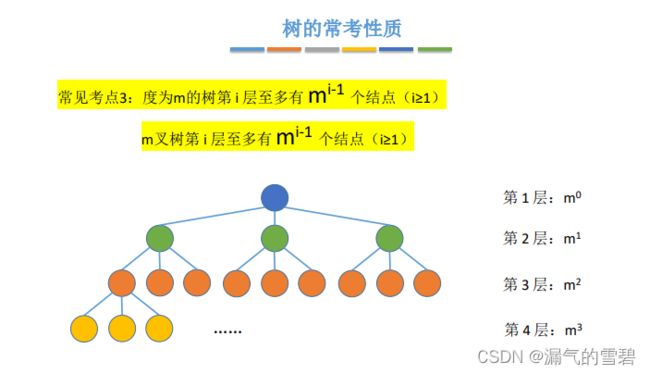
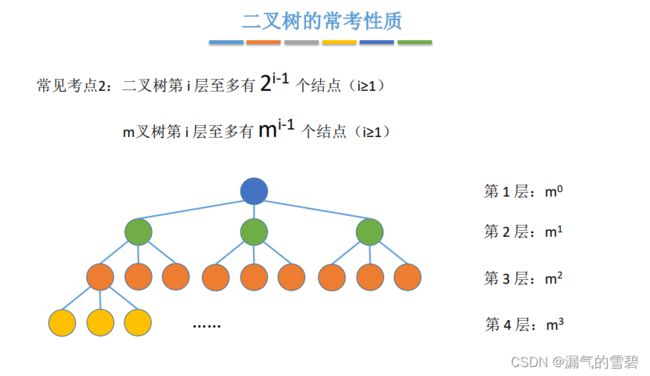
- 1:m^0
- 2:1 * m
- 3:1 * m * m
- n:m ^ (n-1)
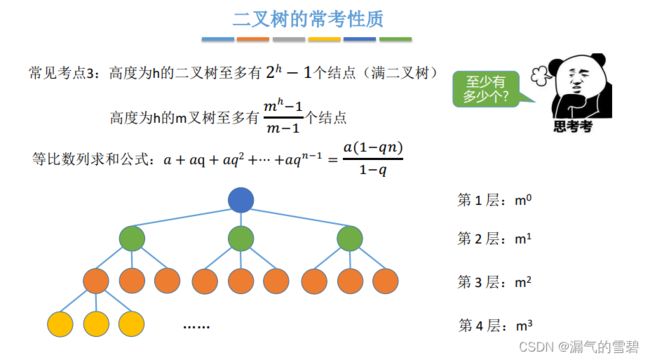
- 在考点3的基础上,等比数列求和
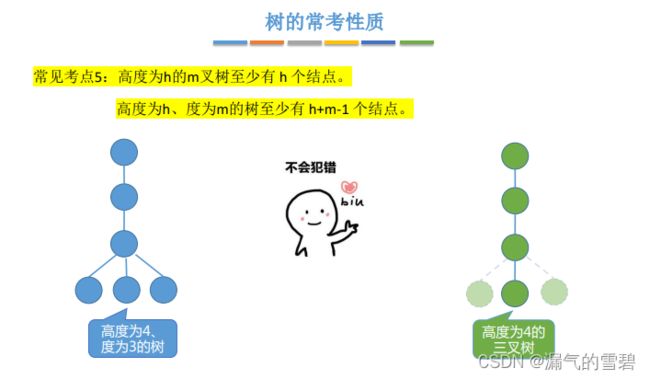
- 高h的 “m叉树” 至少结点数:h
- 高h的 “度为m树” 至少结点数:h+m-1
- 借助考点4的知识,高度为h的m叉树的最大结点数
- 注意!向上取整
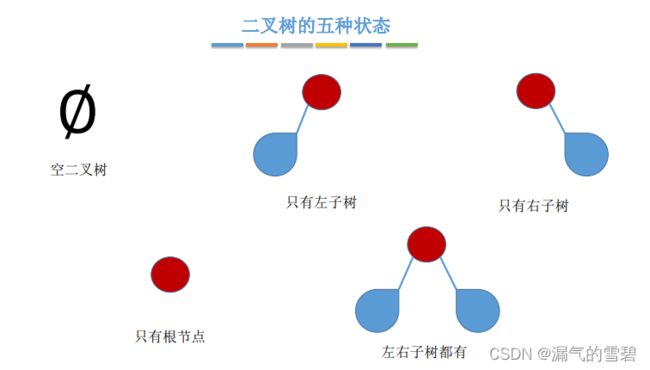
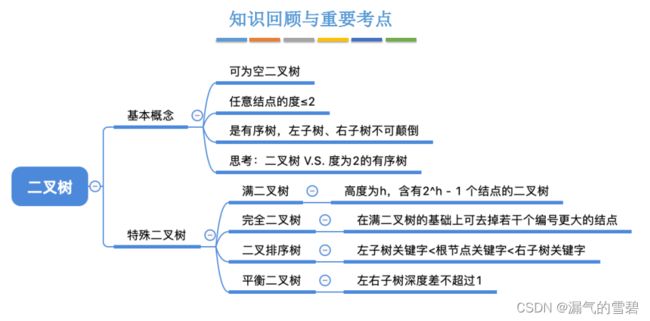
5.1.4 二叉树的定义
- m(m=2)叉树,可以为空(n=2)
- 注意1:和 “度为2” 的树区别
- 注意2:二叉树是有序树,那么就说明左右子树不能颠倒
5.2 二叉树的性质和存储结构
5.2.1 几种特殊的二叉树
1.满二叉树
- 每一层都是满的
- 只有最后一层有叶子结点
- 不存在度为1的结点
- 结点 i 的左孩子为 2i,右孩子为 2i+1
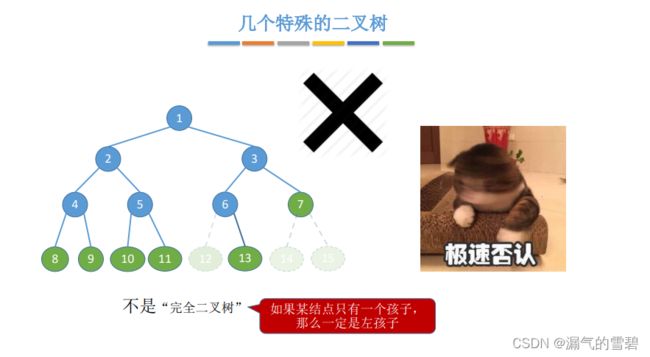
2.完全二叉树
- 在满2叉树的基础上,从最后一个结点开始去掉结点。
- 只有最后两层有叶子结点
- 你可以试一下,只能有一个结点的度为1(或者没有)
- 结点 i 的左孩子为 2i,右孩子为 2i+1
- 分支结点 和 叶子结点 的 “分界线” 可以知道 —— n/2
- 从后往前删除结点,肯定先删除的右孩子,故剩下的左孩子
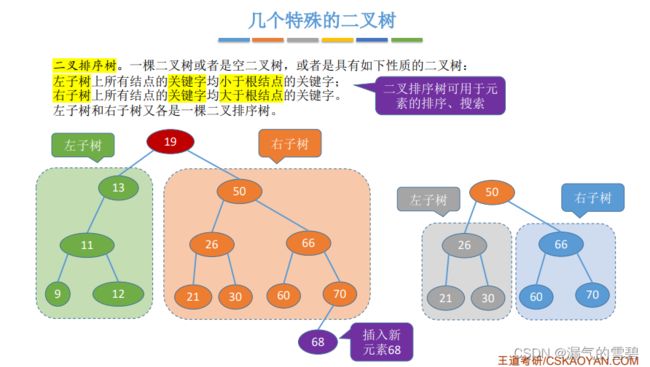
3.二叉排序树
- 前面介绍的满二叉树、完全二叉树是在形态上的特殊二叉树
- 二叉排序树是在功能上特殊的二叉排序树
- 左 < 根 < 右
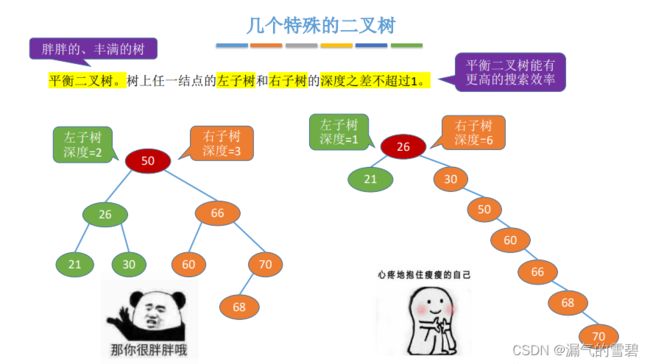
4.平衡二叉树
- |左子树高度(深度)- 右子树| <= 1
- 从下面的图可以看出来,左边平衡二叉树的搜索效率更高
5.小结
5.2.2 二叉树的性质
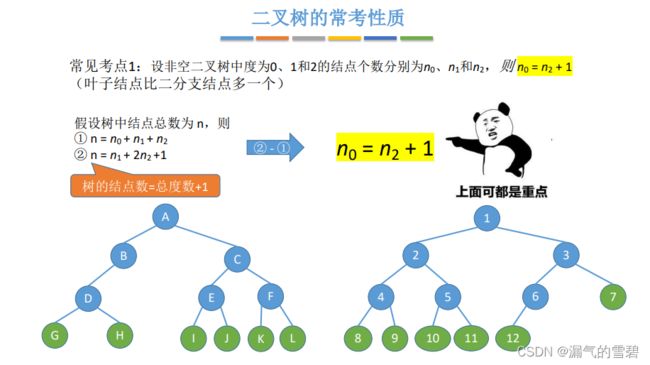
1.二叉树的参考性质
- 联立下面的两个方程得知:叶子结点的数量 比 度为2结点的数量 多一个
- 这个之前介绍过了,等比数列嘛,懂得都懂!
- 还是之前介绍过了,等比数列求和
2.完全二叉树的参考性质
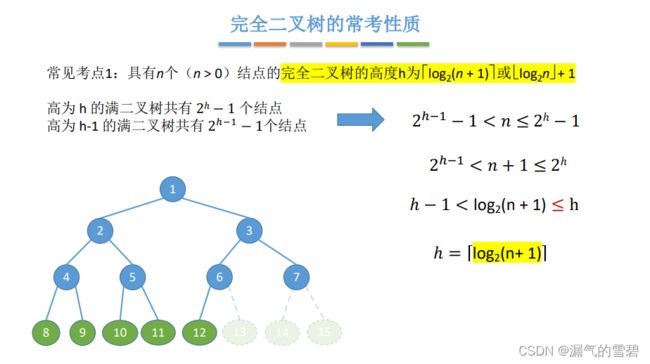
- 方法一:注意向上取整
- 等号在哪,往哪取整!
- 方法二:注意向下取整
- 等号在哪,往哪取整!
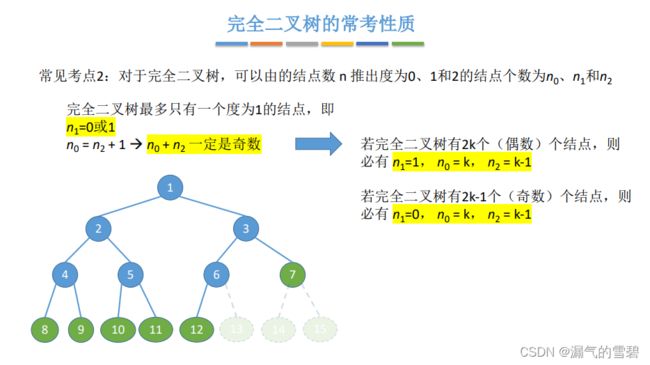
- 完全二叉树中,度为1的结点只能有一个(或者没有)
- 那么可以知道,结点数为偶数,有一个度为1的结点
- 结点数为奇数,没有度为1的结点
- 叶子结点数 - 度为2的结点数 = 1
- 结合上面的分析,就可以得到下图中的结论
3.小结
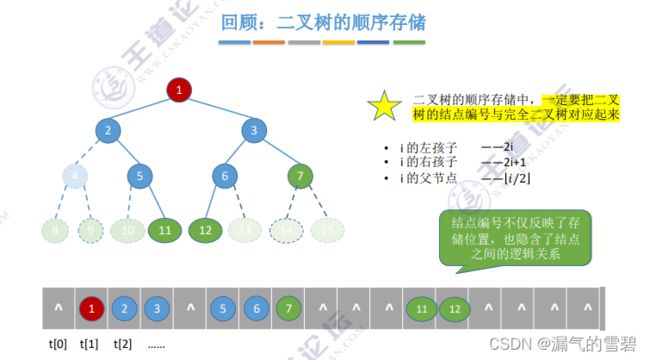
5.2.3 二叉树的存储结构
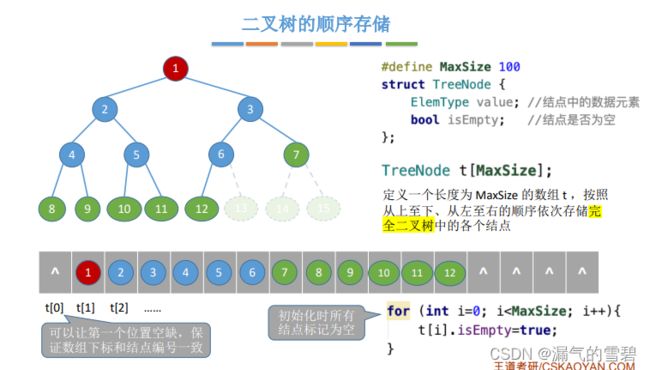
1.顺序存储
1)算法思想
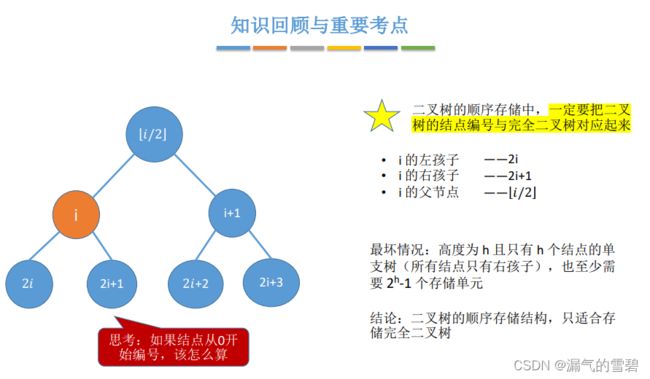
- tree[0]空着,方便后序操作,例如左孩子(i/2),右孩子(i/2+1)
- 结点结构体里的 bool 属性,为true说明为空
2)代码实现
#include
using namespace std;
// ? 本代码实现对二叉树的顺序存储结构
// ? 适合存储完全二叉树的情况
#define MAX_SIZE 100
// ! 顺序存储结点的数组结点
struct TreeNode
{
int value; // 结点中的数据元素
bool isEmpty; // 结点是否为空 (true为空)
};
// ! 初始化静态数组树
// ! 数组当形参时,就是传引用
void InitTreeNode(TreeNode t[])
{
for (int i = 0; i < MAX_SIZE; i++)
{
t[i].isEmpty = true; // 初始化时所有结点标记为空
}
}
int main()
{
TreeNode t[MAX_SIZE]; // 声明一个顺序存储表
InitTreeNode(t); // 初始化顺序存储表
// ! 此时t就相当于一颗二叉树
}
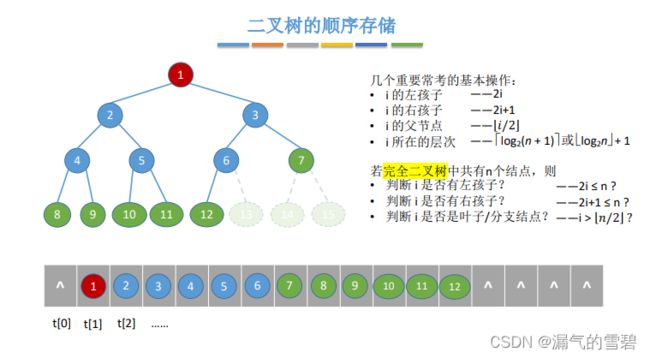
3)算法分析
- 这些我就不一一介绍了
- 需要注意一下第i个结点所在的层次,看不懂的话就去看 “二叉树的性质” 那一小节
- 顺序存储 对于 非完全二叉树 的存储情况很不友好
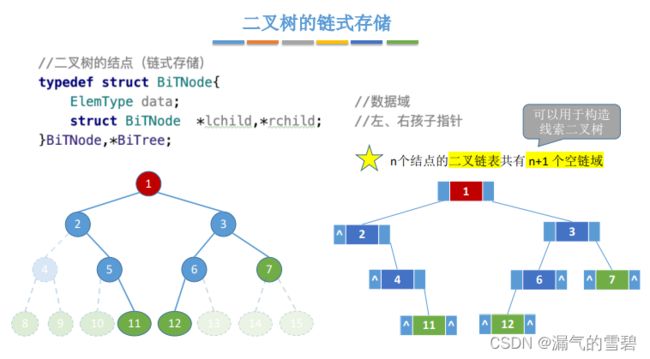
2.链式存储
1)算法思想
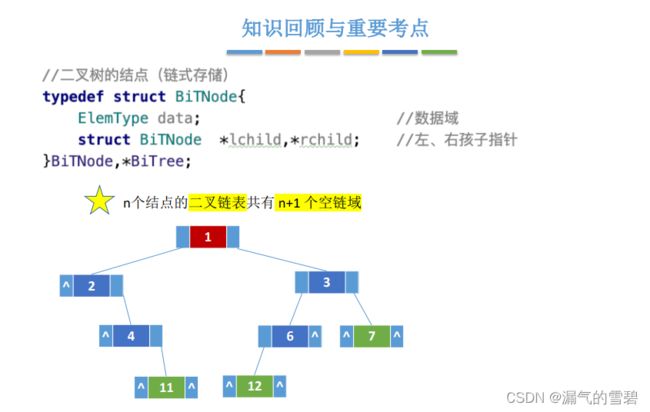
- !!!n个结点的二叉链表共有n+1个空链域(你数数下图中空指针,发现确实是n+1个)
- !!!这些空指针域是有大用处的,具体在线索二叉树那块介绍
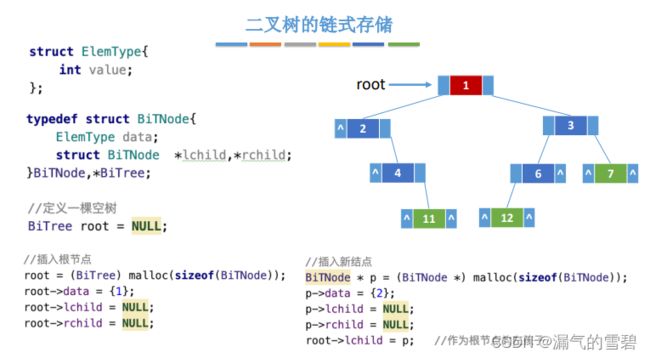
2)代码实现
// ? 链式存储的结点结构体
typedef struct BiTNode
{
ElemType data;
struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;
// 定义一颗空树
BiTree root = NULL;
root = (BiTree)malloc(sizeof(BiTNode));
// 定义一个二叉树结点
BiTnode *p = (BiTNode *)malloc(sizeof(BiTNode));
/*
从上面可以看出 BiTNode 和 *BiTree的区别。
分析下 root
1、它并不是二叉树结点,它是指向一个二叉树结点。
2、它不仅仅代表一个二叉树结点,实际象征着一棵链式二叉树
p才真正代表一个二叉树结点指针
*/
3)算法分析
- 链式存储的结点里,因为存在左、右孩子指针,所以找左、右孩子十分方便
- 对比顺序存储找左、右孩子(完全二叉树情况),顺序存储是(i/2,i/2+1),也挺方便的
- 但是,找父结点就不太方便了(考研中一般考不带父指针的情况)
![]()
3)小结
5.3 遍历二叉树和线索二叉树
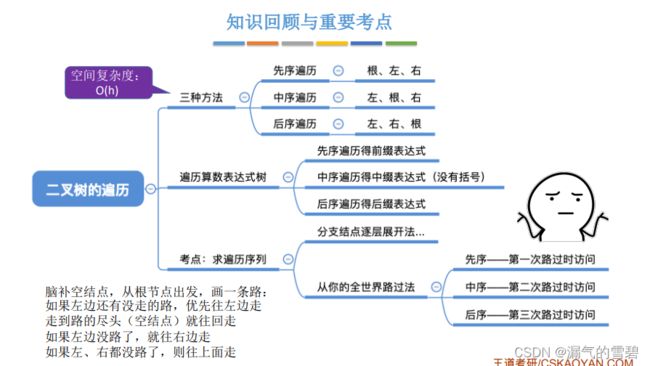
5.3.1 遍历二叉树
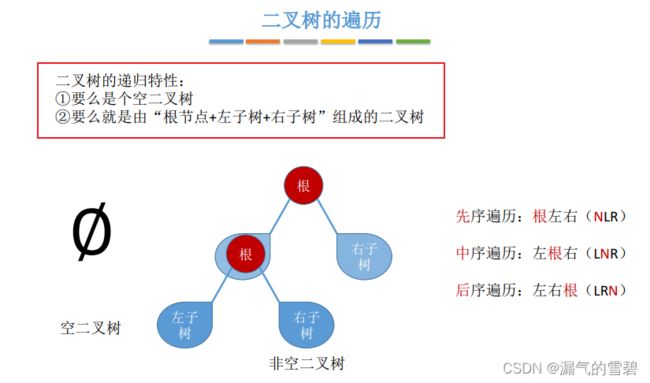
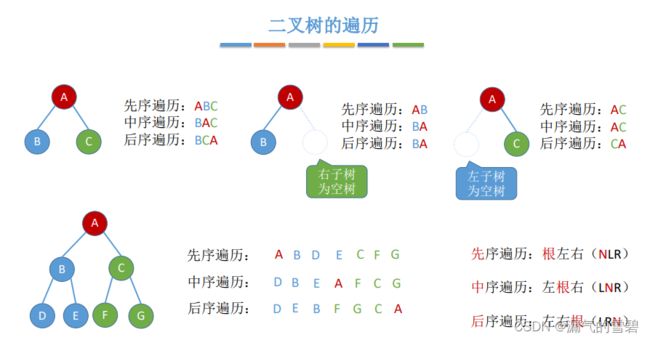
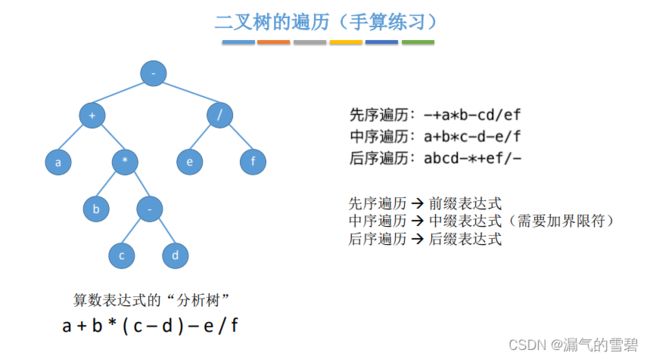
1.算法思想
- 先序遍历:根 --> 左 --> 右
- 中序遍历:左 --> 根 --> 右
- 后序遍历:左 --> 右 --> 根
2.代码实现 - 先中后
#include
using namespace std;
// ? 本代码实现二叉树DualTree的链式存储
// ! 实验数据: -+a##*b##-c##d##/e##f##
// ! 二叉树结点
typedef struct BiTNode
{
char data; // 数据域
struct BiTNode *lchild, *rchild; // 指针域:左、右孩子指针
} BiTNode, *BiTree;
// ! 初始化二叉树
void InitTreeRoot(BiTree &root)
{
root = NULL;
}
// ! 添加新结点
void InsertBiTNode(BiTree &root)
{
char ch;
cin >> ch;
if (ch == '#')
{
root = NULL;
}
else
{
root = (BiTree)malloc(sizeof(BiTree));
root->data = ch;
InsertBiTNode(root->lchild);
InsertBiTNode(root->rchild);
}
}
// ! 先序遍历
void ProOrder(BiTree root)
{
if (root == NULL)
{
return;
}
cout << root->data << " ";
ProOrder(root->lchild);
ProOrder(root->rchild);
}
// ! 中序遍历
void MiddleOrder(BiTree root)
{
if (root == NULL)
{
return;
}
MiddleOrder(root->lchild);
cout << root->data << " ";
MiddleOrder(root->rchild);
}
// ! 后序遍历
void PostOrder(BiTree root)
{
if (root == NULL)
{
return;
}
PostOrder(root->lchild);
PostOrder(root->rchild);
cout << root->data << " ";
}
int main()
{
BiTree biTree;
InitTreeRoot(biTree);
InsertBiTNode(biTree);
cout << "先 序 遍 历: ";
ProOrder(biTree);
cout << endl
<< "中 序 遍 历: ";
MiddleOrder(biTree);
cout << endl
<< "后 序 遍 历: ";
PostOrder(biTree);
cout << endl
<< "树的深度:" << TreeDepth(biTree);
return 0;
}
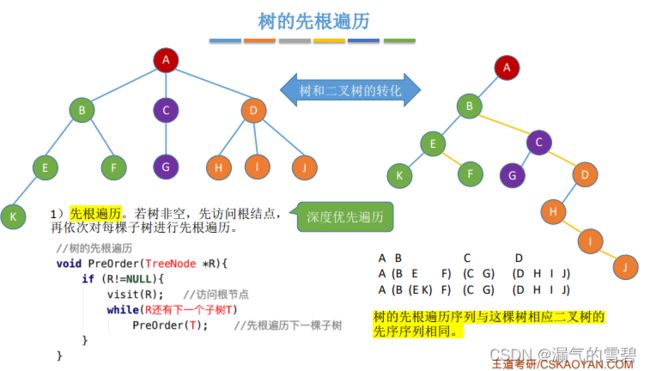
3.先序遍历
- visit(BiTree T) 函数可以定义一下自己想要的操作,例如打印输出
- 空间复杂度:O( h + 1 ),h为高度,+1是处理最后的空结点(+1可以舍去)
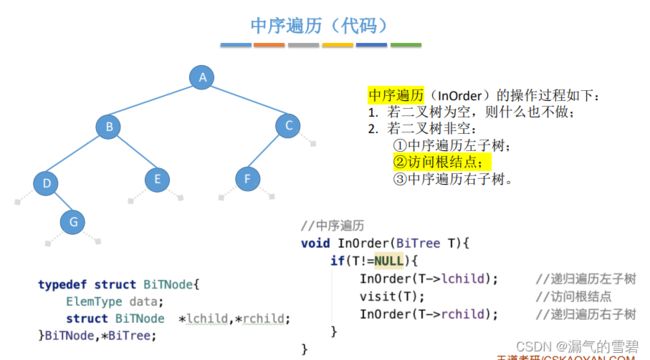
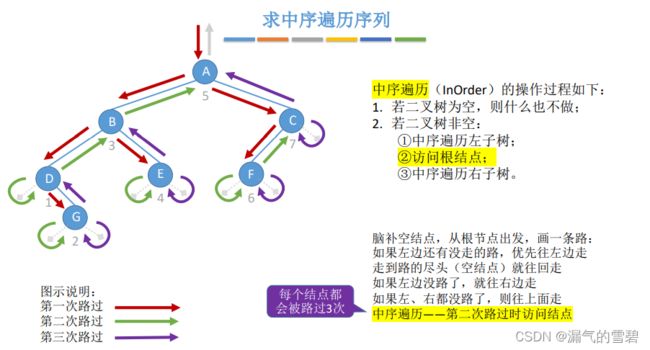
4.中序遍历
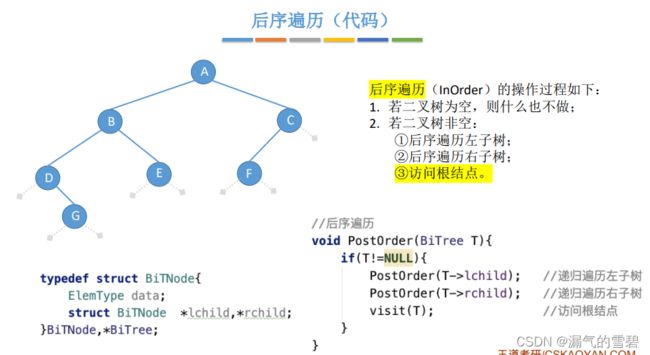
5.后序遍历
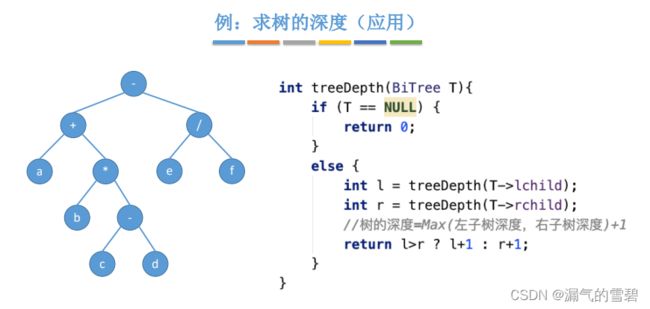
6.树的深度
// ! 求树的深度
int TreeDepth(BiTree root)
{
if (root == NULL)
{
return 0;
}
int l = TreeDepth(root->lchild);
int r = TreeDepth(root->rchild);
return l > r ? l + 1 : r + 1;
}
7.层次遍历
1)算法思想
2)代码实现
// ? 下面实现二叉树的层序遍历
// ! 链式队列结点
typedef struct LinkNode
{
BiTNode *data; // 此处代表的含义是指针,不是结点;与二叉树不同,看下图对比
struct LinkNode *next;
} LinkNode;
// ! 辅助队列
typedef struct
{
LinkNode *front, *rear; // 队列的对头、队尾
} LinkQueue;
void LevelOrder(BiTree root)
{
LinkQueue Q;
// ……
}
- 使用辅助队列,而且并不是存入结点,而是存入指向该结点的指针
8.小结
5.3.2 根据遍历序列确定二叉树
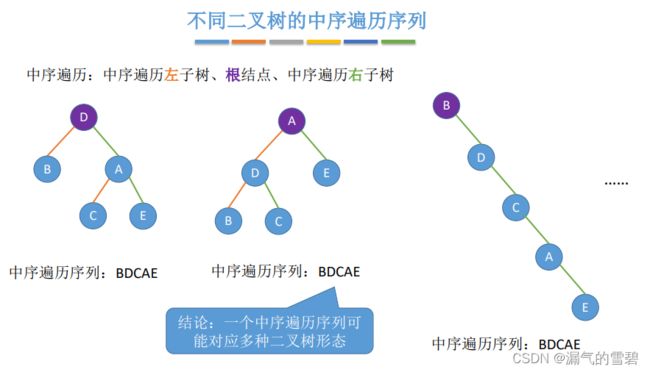
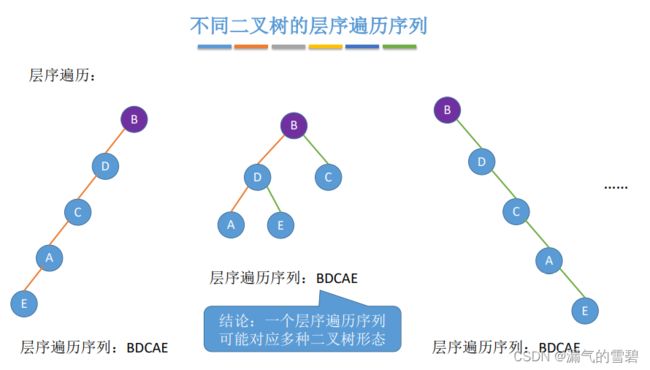
1.单个遍历序列确定二叉树
- ① 中序遍历可以对应多种形态 (不唯一)
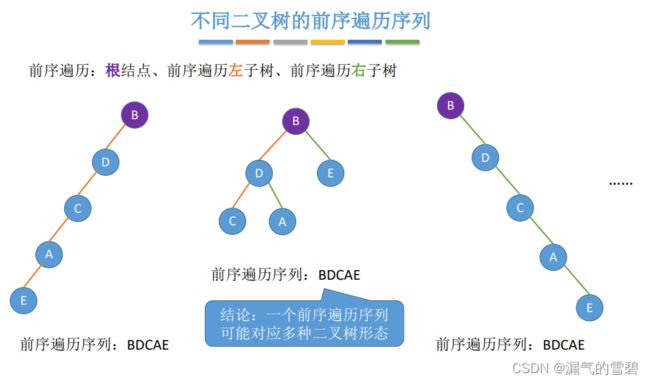
- ② 前序遍历可以对应多种形态 (不唯一)
- ③ 后序遍历可以对应多种形态 (不唯一)
![]()
- ④ 层序遍历也会对应多种不同形态的二叉树(不唯一)
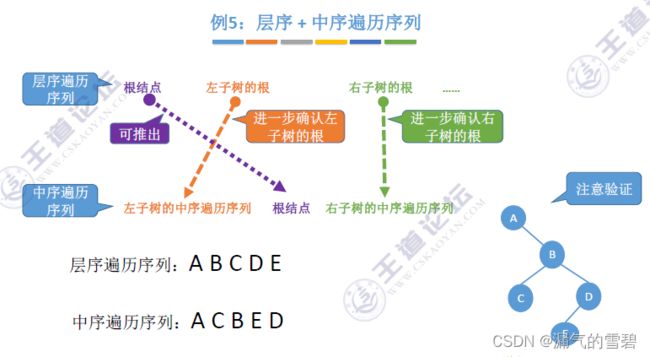
- ⑤ 结论 - 关键:中序遍历
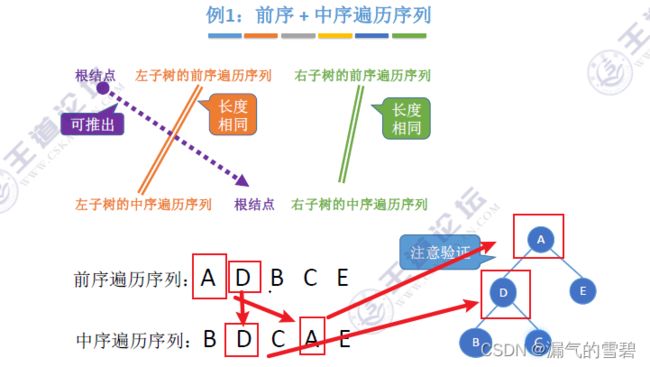
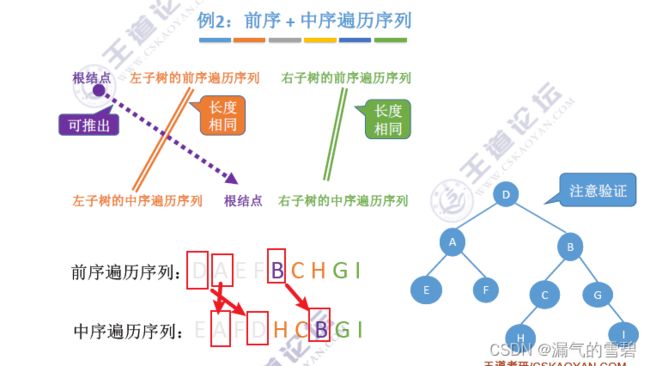
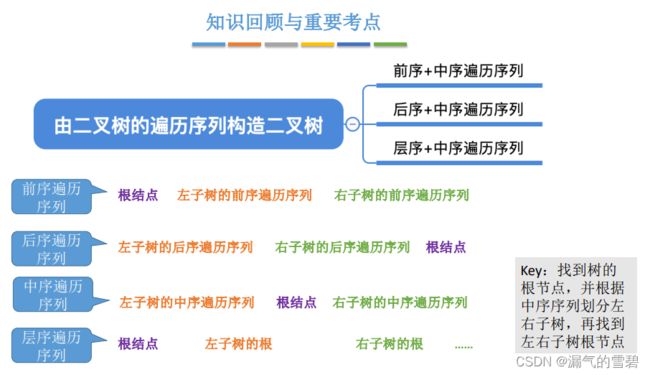
2.算法思想 - 举例
- 前序第一个元素,A为根结点,那么可以把中序序列划分成左、右子树了
- 并且通过中序序列,可以知道左、右子树各自的结点数(看A的位置)
- 元素D,为左子树的根结点,再进一步划分
3.小结
- 在这4种构造二叉树的问题中,其实都是对 中序序列 的划分
- 使用 前序 去划分中序
- 使用 后序 去划分中序
- 使用 层序 去划分中序
- !!!这一小节老师没有提到代码,课后自己可以尝试补充!!!
- 没有中序序列,不能构造二叉树
5.3.3 线索二叉树
1.前言
- 之前二叉树的缺点
- 1、必须从根结点开始遍历,不能从指定结点开始
- 2、找前驱、后继很麻烦(从头遍历 + 辅助指针pre)
- 为什么找后继也很麻烦呢?
- 后继和孩子结点不同
- 因为我们此时是从中序遍历序列去指定一个结点,例如G,如果要找G的后继:
- 1、需要sub指针
- 2、当q指针找到p(q==p,有传入p指针当参数的情况),sub才能记录p的后继
- 3、如果没有插入p指针,就对比结点里的数据是否相等
- 想要下图的过程代码,跳到5.3.4二叉树线索化 1.老办法小节
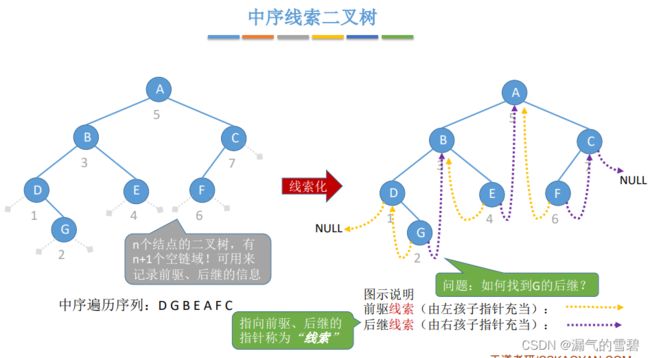
2.线索二叉树的基本概念
-
之前在二叉树的链式存储小结提到:n个结点的二叉树有n+1个空链域,就是用在二叉树线索化中
-
左孩子指针 - 存储前驱线索
-
右孩子指针 - 存储后继线索
-
注意了!!!注意,此时我们提到的前驱、后继是中序遍历序列里的前驱、后继。和二叉树结点的前驱(双亲)和后继(子孙)不一样。
-
所以,看下面的图中,D的左孩子指针为NULL,因为D在中序遍历序列里面没有前驱
-
再一次注意了!有右孩子的时候,右孩子也不一定是后继,比如AC,A的后继是F
-
再举个例子,看BE,如果E的左子树不为空,那么B的后继就不是E了
-
接着上一行的问题,如果一个结点的右孩子指针指向右孩子,而不是后继线索,那么如何查找后继呢?
-
答案会在5.3.5 线索二叉树的使用里介绍
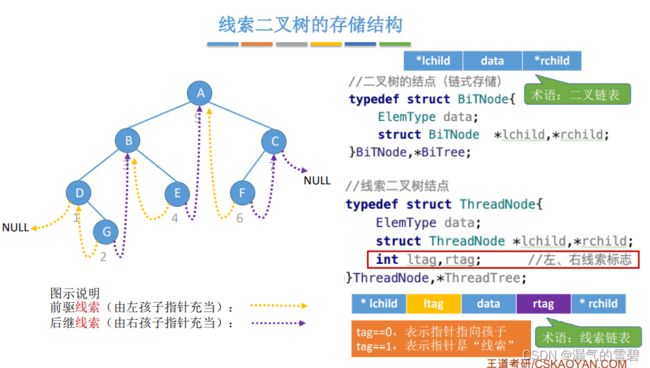
3.线索二叉树的存储结构
// 左、右线索标志
typedef struct ThreadNode{
ElemType data;
struct ThreadNode *lchild, *rchild;
int lTag, rTag; // 0指向孩子;1指向线索
}
// 此时可以叫做线索链表
- 从1到3小节,都是以“中序线索二叉树的构造”举例介绍线索二叉树的思想,下一小节里就只介绍先序、后序线索二叉树了
4.线索二叉树的构造
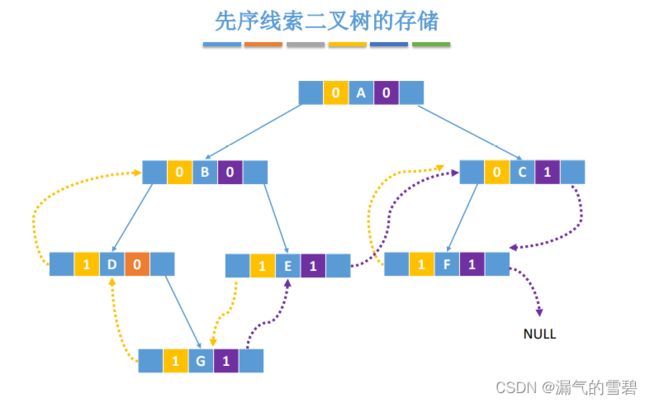
- ① 先序线索二叉树
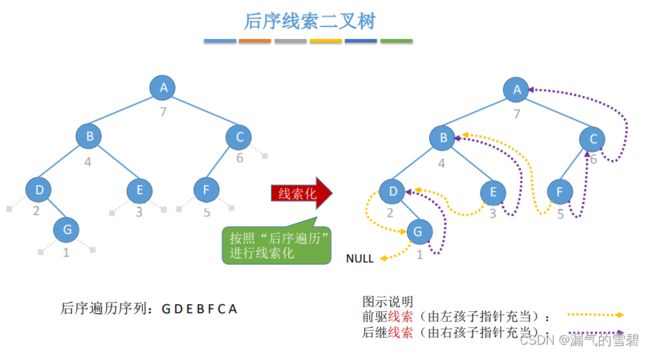
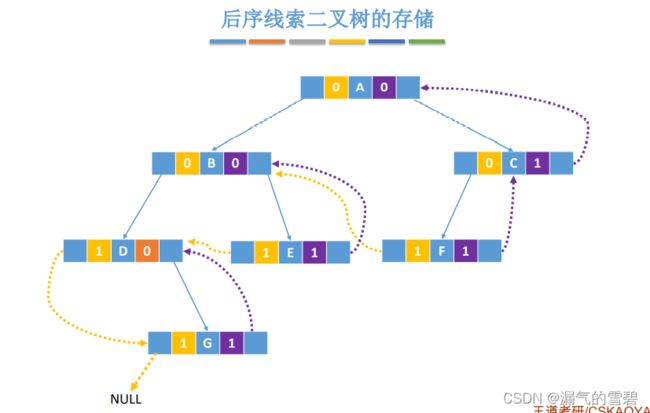
- ② 后序线索二叉树
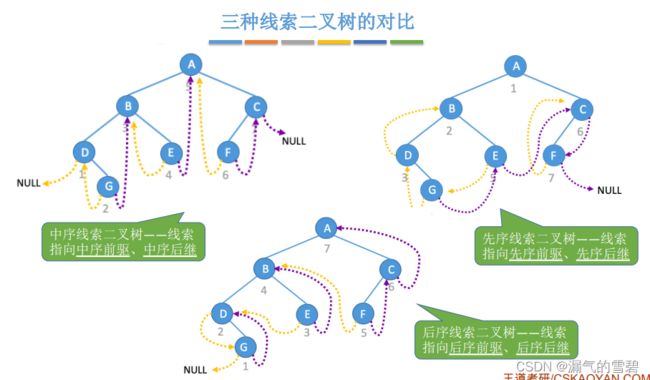
- ③ 三种线索二叉树的对比
5.3.4 二叉树线索化
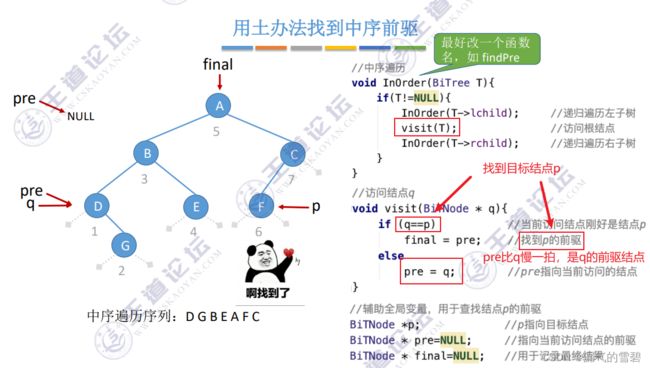
1.老办法
- 如果对于老办法还不太清楚的话,去5.3.3线索二叉树 1.前言小节,有具体介绍
// 辅助全局变量,用于查找结点p的前驱
BiTNode *; // p指向目的结点
BiTNode *pre = NULL; // 指向点前访问结点的前驱
BiTNode *final = NULL; // 用于记录最终结果
// 访问结点q
void visit(BiTNode *q) {,
if (q==p)
final = pre;
else
pre = q;
}
// 寻找中序前驱就少不了中序遍历
void FindPre(BiTree T) {
if (T!=NULL) {
InOrder(T->lchild);
visit(T);
InOrder(T->rchild);
}
}
2.中序线索化
这里重点介绍中序线索化,后面的先序、后序线索化思想类似,就不会再大量描述了
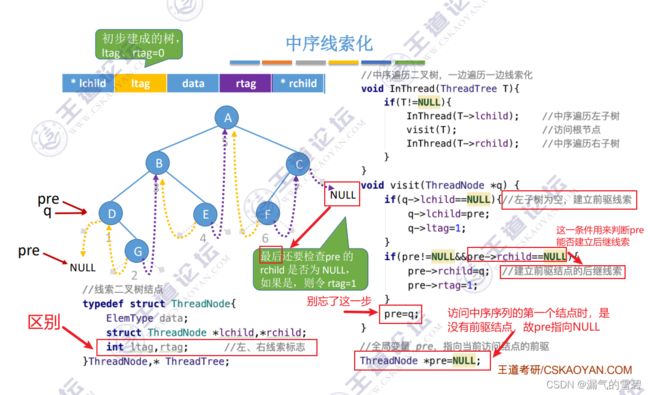
1)算法思想
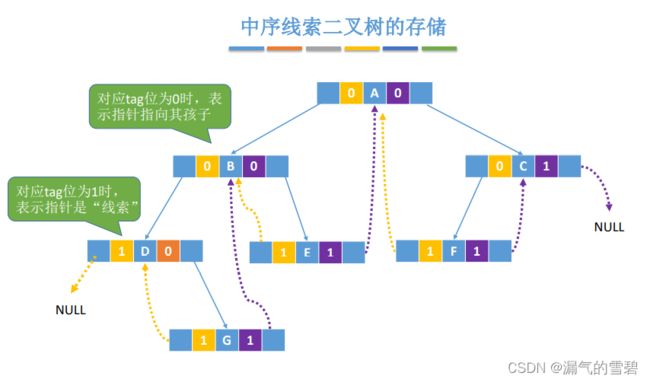
- 线索二叉树的结点结构体里有标志位属性
- 最后线索化结束了,还没有将C的右孩子指针还没线索化
- 可以借助pre是全局变量的特性,并且最后pre就是指向C结点,通过pre对rchild设置为NULL,rTag也得为1,因为这是一颗被线索化过的二叉树
2)代码实现
3)算法分析
- 思考:处理遍历的最后一个结点(结点i)时,为什么没有判断rchild是否为空?
- 回答:中序遍历的顺序:左-根-右。如果最后遍历的结点有右孩子,那么还会接着遍历,因为是左-根-右。此时结点i就是根,左孩子已经先一步遍历完了。
- 上面的解释如果觉得看不懂得话,就换一种思路,问:最后一个结点可以有左、右孩子吗?
- 左孩子,可以。因为遍历顺序左-根-右,最后一个结点得左孩子已经遍历完了,不影响。
- 右孩子,不可以。因为还得接着遍历,这样这个结点就不是最后一个结点了,矛盾。
3.先序线索化
4.后序线索化
5.小结
5.3.5 线索二叉树的使用
1.中序线索二叉树
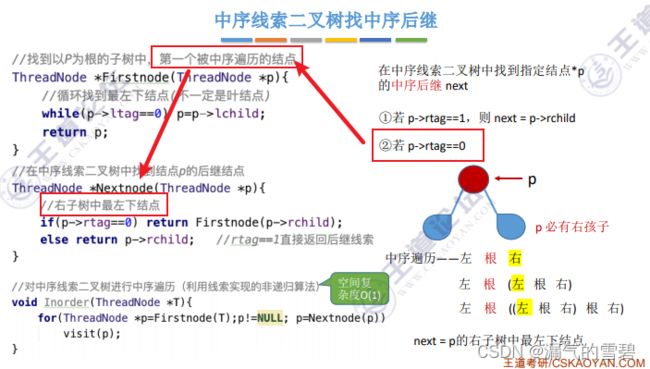
1)找中序后继
- 在中序线索二叉树中,如果p->rTag==1,右孩子指针被线索化了,那么直接得到中序后继
- 若p->rTag==0,有右孩子。就要找右子树得中序遍历最左边的结点
![]()
-
FirstNode(ThreadNode *p)函数:得到以p为根的子树中,第一个被中序遍历的结点(会去找左下角)
-
NextNode(ThreadNode *p)函数:得到p结点在中序遍历里的后继结点
-
那么借助上面两个函数就能对二叉树进行中序遍历了:
- 1、先使用第一个函数得到第一个被中序遍历的结点
- 2、以这个结点开始,给第二个函数传入传参数,得到一下个中序遍历的结点,以此类推
-
这种使用for循环的中序遍历二叉树,空间复杂度只需要O(1)
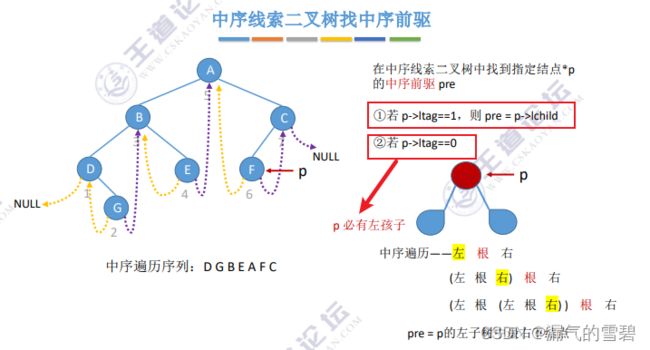
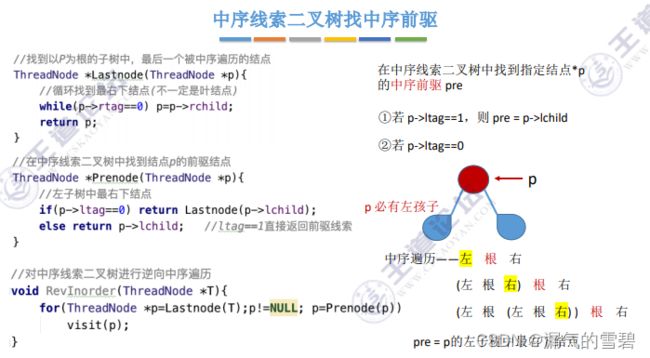
2)找中序前驱
- 和找中序后序的思想差不多,就不再写了
- 找左子树的最右边的结点(左-根-右)
2.先序线索二叉树
1)找先序后继
- 1、当rTag为1,被线索化,直接指向先序后继
- 2、当rTag为0,指向右孩子,可以知道p有右孩子,但不确定有没有左孩子。此时就需要分情况讨论了:
- ① 有左孩子,先序后继就是左孩子自己(根-左-右)
- ② 没有左孩子,先序后继就是右孩子自己(根-左-右)
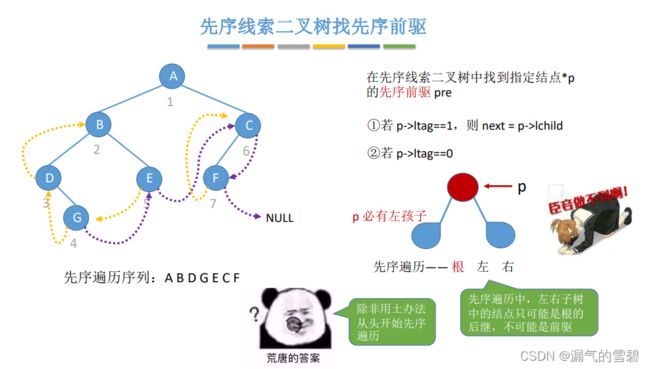
2)找先序前驱
- ltag==1,左孩子被线索化,直接得到先序前驱
- ltag==0,有左孩子。根据先序遍历的顺序(根-左-右),p的左、右子树遍历的元素都只能是p的后继,故得不到p的前驱。
- 硬要找的话,只能使用土办法
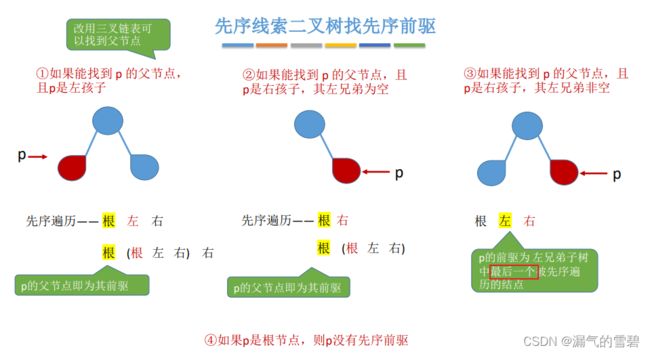
- 上面说到先序线索二叉树找先序前驱实现不了,那如果加一个条件,多一个p的父结点,此时还能找到p的先序前驱吗?—— 看一下图
- 下图中红色的结点就是p的位置,下图分了4种p可能出现的位置讨论
3.后序线索二叉树
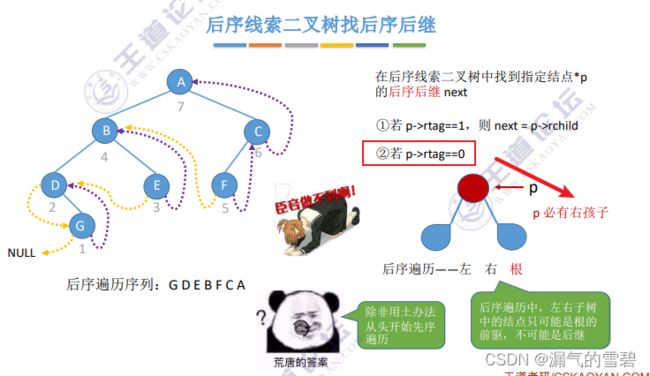
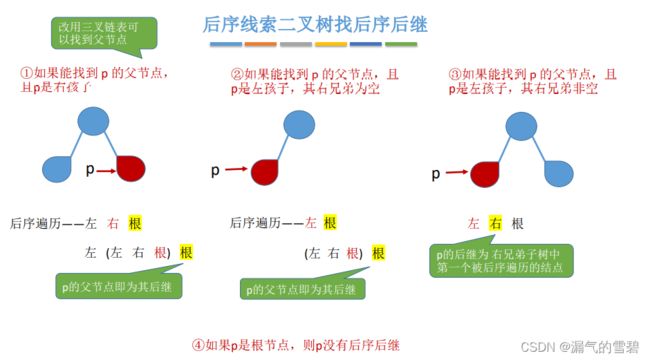
1)找后序后继
- 1、当rTag为1,被线索化,直接指向后序后继
- 2、当rTag为0时,有右孩子。因为后序遍历(左-右-根),那么左、右子树结点只能是p的前驱,所以无法再后序线索二叉树种找到p的后序后继。
- 3、硬找的话:土办法
- 上面说到后序线索二叉树找先序后继实现不了,那如果加一个条件,多一个p的父结点,此时还能找到p的先序后继吗?—— 看一下图
- 下图中红色的结点就是p的位置,下图分了4种p可能出现的位置讨论
2)找后序前驱
- 1、lTag==1,左孩子被线索化,直接得到后序前驱
- 2、lTag==0,有左孩子结点。因为不清楚有没有右孩子,需要分情况讨论:
- ① 、有右孩子,根据后序遍历顺序(左-右-根p),p的后序前序就是它的右孩子
- ② 、没有右孩子,(左-空-根p),p的后序前驱就是它的左孩子
- ③ 、①和②虽然都得再一次分别对右子树、左子树进行后序遍历,但根据(左右根),最靠近p的还是左、右儿子结点
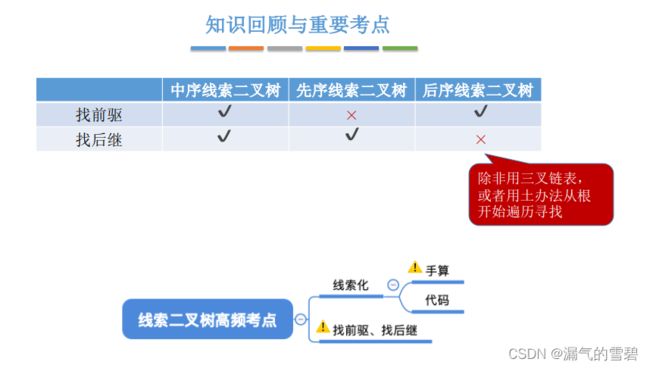
4.小结
5.4 树和森林
5.4.1 树的存储结构
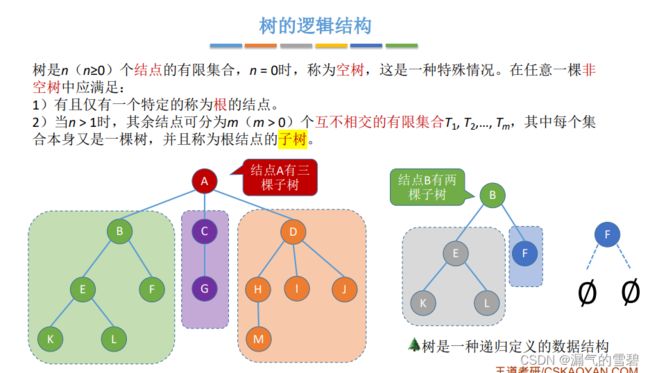
1.树的逻辑结构回顾
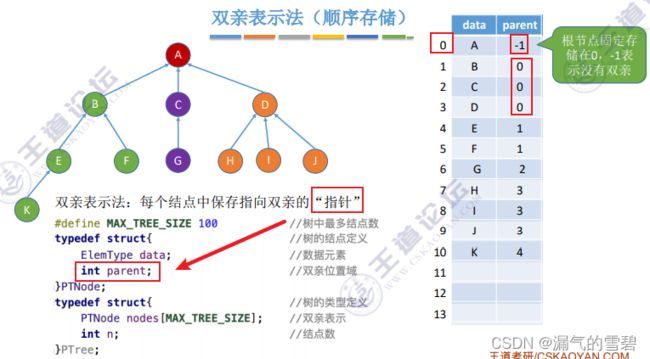
2.双亲表示法 - 顺序
1)算法思想
- 双亲表示法,注意和之前二叉树的顺序存储(适用于完全二叉树)之间的区别
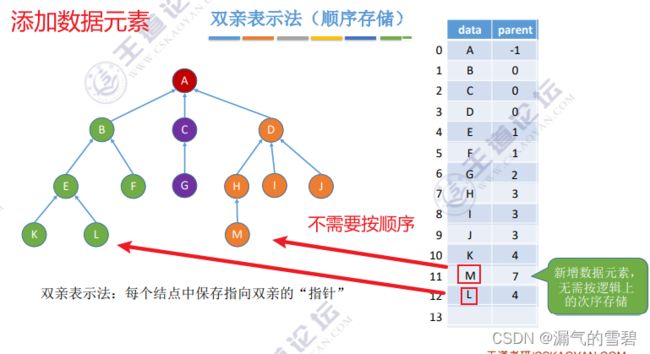
2)增、删操作
-
① 增
-
直接在存储数组的末尾添加元素即可,不需要按照层序遍历顺序
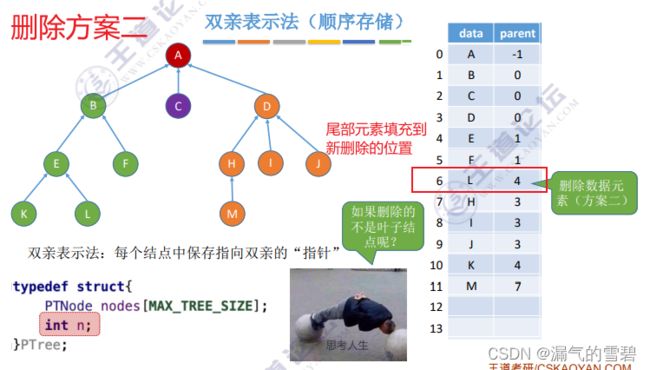
- ② 删
- 直接将该结点的数据域清空,指针域设置为-1
- 这种删除方案有缺陷,如果删除过多元素的话,那么使得数组里的空数据较多,减低检索速率
- 清空数组表里对于元素的数据域和指针域,再把最底下的元素上移填充空白
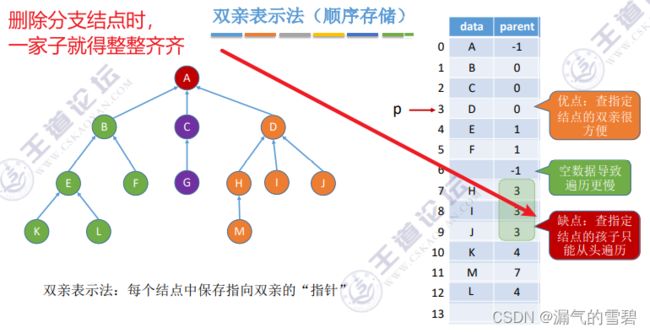
- 查找操作:
- ① 查找p的双亲时,十分简单
- ② 查找p的子孙时,需要将数组遍历,查找双亲是p的结点,很不方便
- 当删除分支结点的时候,不只是删除一个结点那么简单,得把子孙结点通通删除
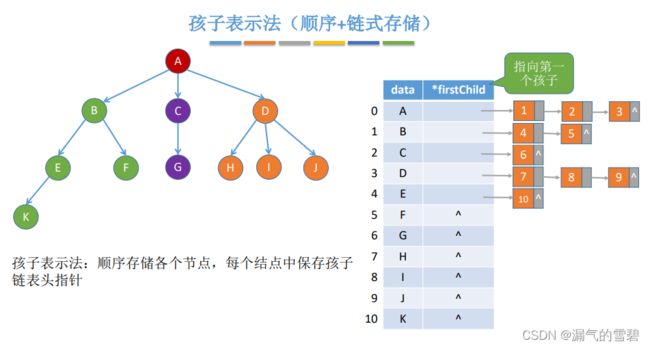
3.孩子表示法 - 顺序 + 链式
- 有几个结点,数组就有几个元素
- 数组元素的指针域指向第一个孩子结点
- 孩子结点结构(数据域,指针域)
// 链结点
struct CTNode {
int child; // 孩子结点在数组的位置
struct CTNode *next; // 下一个孩子
};
// 数组结点
typedef struct {
ElemType data;
struct CTNode *firstChild; // 第一个孩子
} CTBox;
// 孩子表示法的树结构
typedef struct {
CTBox nodes[TREE_INIT_SIZE];
int n, r; // 记录结点数和根的位置
} CTree;
- 找孩子方便,找双亲不太方便
![]()
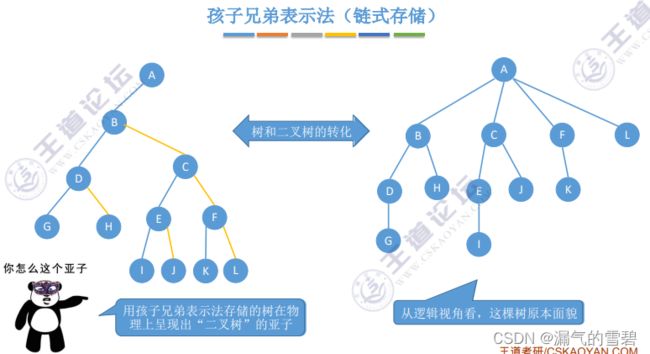
4.孩子兄弟表示法
- 乍一看孩子兄弟表示法的结点结构 和 二叉链表的结点结构,不能说毫不相关吧,只能说是一模一样!
- 它们的区别就在与指针域所表示的意义不同
typedef struct BiTNode{ ElemType data; struct BiTNode *lchild, *rchild; // 左、右孩子指针} BiTNode, *BiTree;typdef struct CSNode{ ElemType data; struct CSNode *firstChild,*nextSibling; // 第一个孩子 和 右兄弟指针} CSNode, *CSTree;
- 在这也可以初步认识 树 --> 二叉树 的转换问题
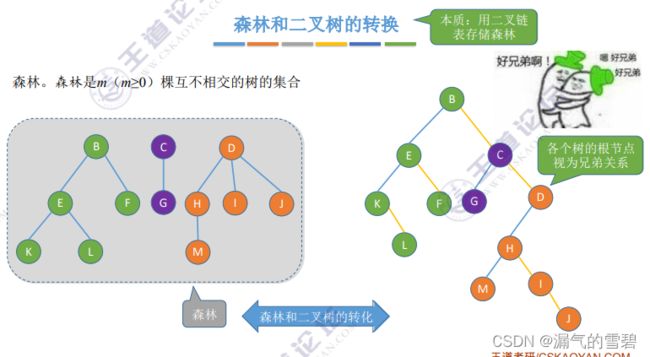
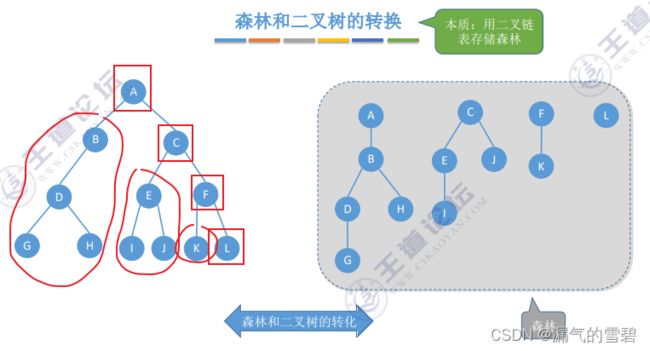
5.树、森林与二叉树的转换
- 1、先将森林里的各棵树使用上面的 “孩子兄弟表示法” 转换一下
- 2、在将转换后的各棵树再使用 “孩子兄弟表示法” 连接起来
- 懂了森林如何转换成二叉树,那么反过来转换也差不多明白了
6.小结
5.4.2 树和森林的遍历
1.树的遍历
- 回顾下树的逻辑结构
- 注意!!!树没有中根遍历,和之前二叉树的中序遍历不一样,因为树可以有很多个分支,怎么中根呢?
1)先根遍历
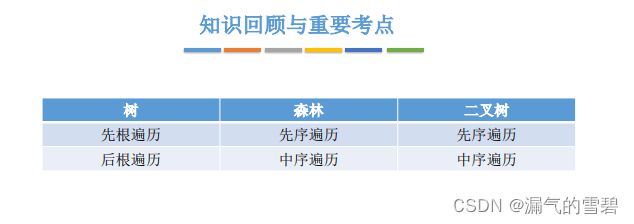
- 重要结论:树的 先根遍历序列 和 对应的二叉树 的先序序列相同
2)后跟遍历
- 重要结论:树的 后根遍历序列 和 对应的二叉树 的中序序列相同 ,对!你没有看错,是中序序列
3)层次遍历
- 层次遍历就是广度优先遍历
- 上面的先根、后根遍历就是深度优先遍历
2.森林的遍历
1)先序遍历
- 森林的先序遍历
- 方法一:依次地对树进行先根遍历(就树比较奇葩,叫先跟,不是先序)
- 森林的先序遍历 - 方法二:
- 1、先将森林转换成对应的二叉树
- 2、对二叉树进行先序遍历
2)中序遍历
- 方法一:依次地对树进行后序遍历(注意!!!森林中序 = 树后根遍历)
- 森林的中序遍历 - 方法二:
- 1、先将森林转换成对应的二叉树
- 2、对二叉树进行中序遍历 (注意!!!森林中序 = 二叉树中序)
![]()
3.小结
- 后序去哪了???
5.5 树和二叉树的应用
5.5.1 二叉排序树(BST)
1.定义
- 二叉排序树:所有结点满足(左 < 根 < 右)
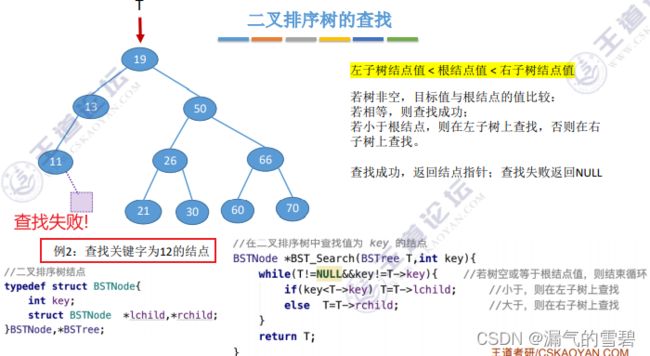
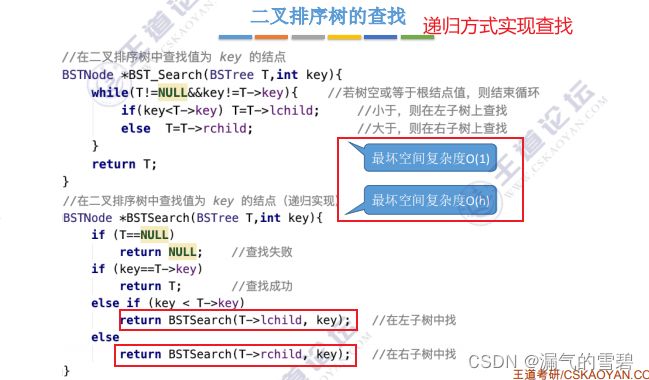
2.查找
- ① 非递归方式实现二叉排序树的查找
- ② 递归方式实现二叉排序树的查找
- O(h)空间复杂度:树高几层 就会 递归几层
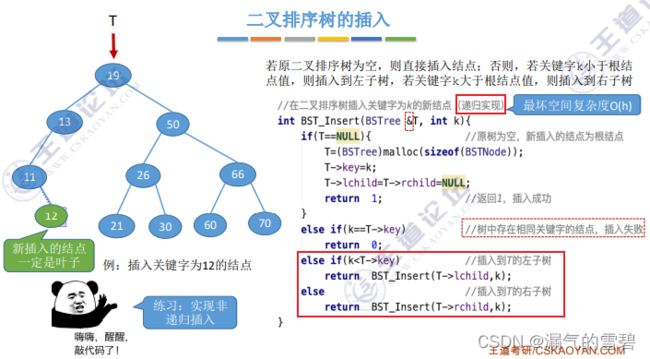
3.插入
- 1、新插入的结点一定是叶子结点(规定的)
- 2、二叉排序树不存在两个关键字相同的结点,如果插入这样的新结点,则插入失败
- 3、为什么插入函数的参数是传引用呢?
- 答:插入函数是先从根结点开始遍历,去寻找合适的位置插入,当找到“11结点”时,需要对该结点的右孩子指针进行修改,那他指向先插入的“12结点”,所以需要传引用参数
- 递归插入最坏空间复杂度:O(h)和树高有关
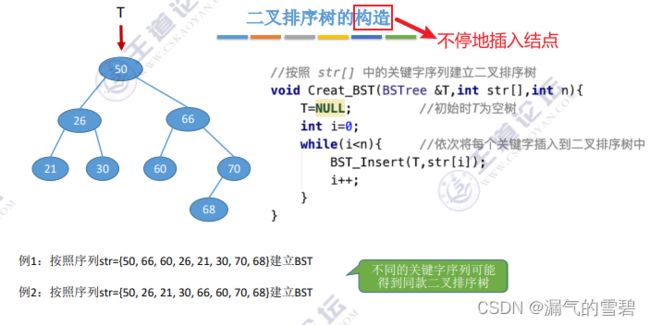
4.构造
- 如何构造二叉排序树呢?
- 答:实际上就相当于不断插入新结点的过程
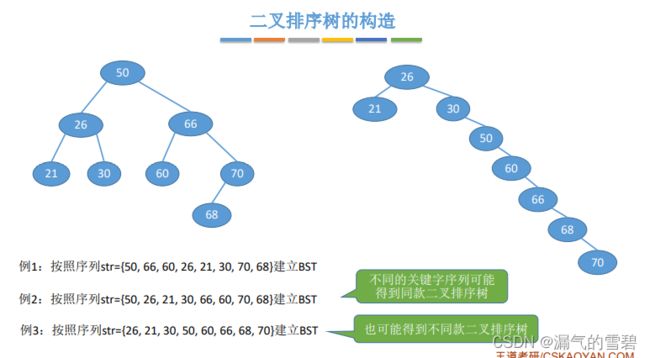
- 有时不同的关键字序列 可以得到 相同的二叉排序树
- 但也可能得到不同的二叉排序树
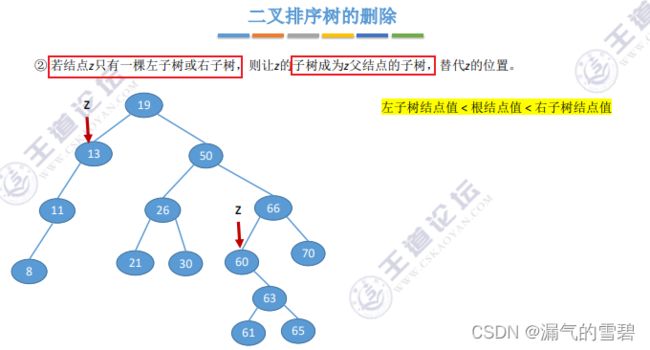
5.删除
- ① 删除度为0(叶子结点),直接删除
- ② 删除度为1的结点时,让其子树替代即可
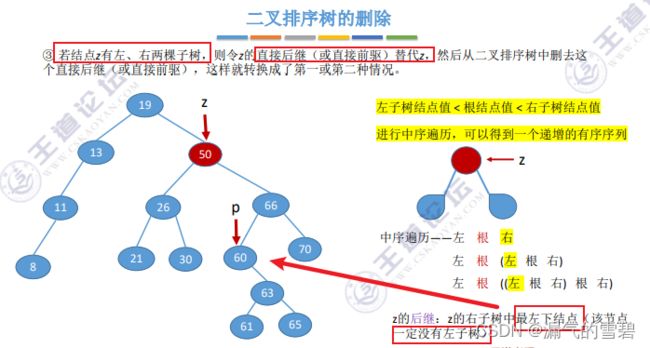
- ③ 删除度为2的结点时,有两种补救措施:
- 1、选择直接后继,右子树最左下结点
- 看下图,既然找到的p是最左下结点,那么它一定没有左子树,可知它的度为1
- 那么p被移动到z除,原先的位置空着,这就相当于上面的删除度为1的结点
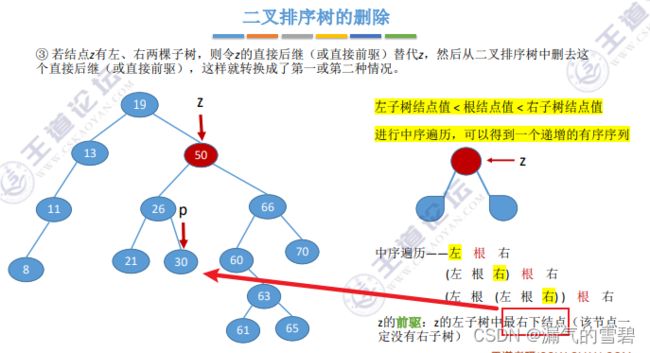
- 2、选择之前前驱,左子树最右下结点
- 看下图,既然找到的p是最右下结点,那么它一定没有右子树
- 而且此时p的度为0,这就相当于上面的删除度为0的结点,直接删除即可
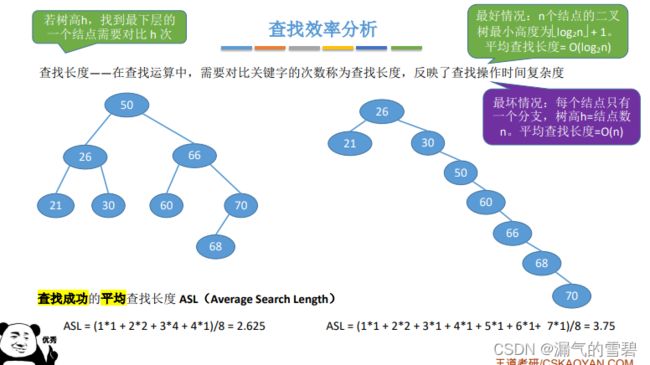
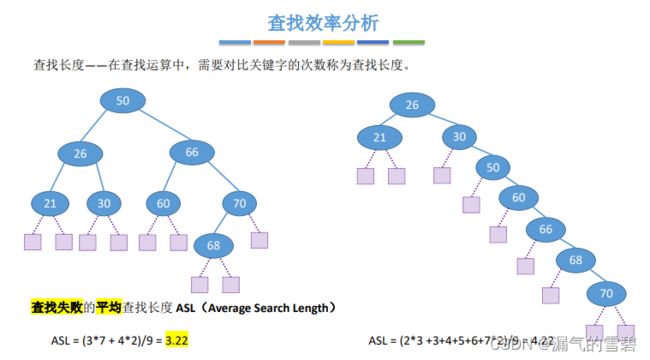
6.查找效率分析
- 平衡二叉排序树的查找效率较高
- 自己分析下如何得到最好、最坏情况下的平均查找长度
- 查找失败的平均查找情况:
- 查找失败时,指针会停留在最底下的空链域处
7.小结
5.5.2 平衡二叉树(AVL)
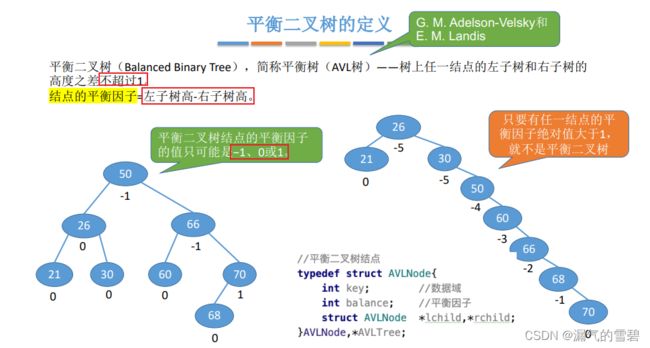
1.定义
- 平衡二叉树经常在选择题里考察
- 专有名词:平衡因子 = 左 - 右(-1,0,1)
typdef struct AVLNode{ int key; // 数据域 int balance; // 平衡因子 struct AVLNode *lchild, *rchild; // 左、右孩子指针}
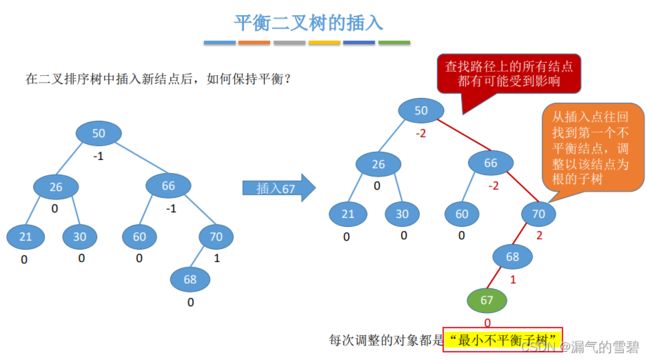
2.插入
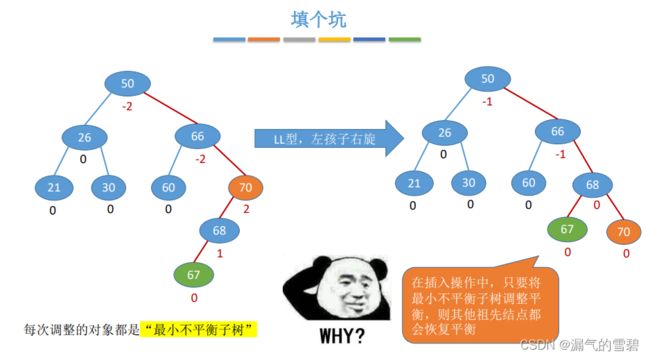
- 当平衡二叉树插入新结点的时候,可能会破坏原本二叉树的平衡,那么就需要去重新调整二叉树,使其恢复平衡
- 解决办法:去调整**“最小”不平衡子树**即可
- 那么怎么找到最小不平衡子树呢?
- 答:以下图举例,才67开始从下往上找,当找到哪个结点的平衡因子不是(-1,0,1)时,也就是找到第一个不平衡结点,这个不平衡结点就是最小不平衡子树的根结点
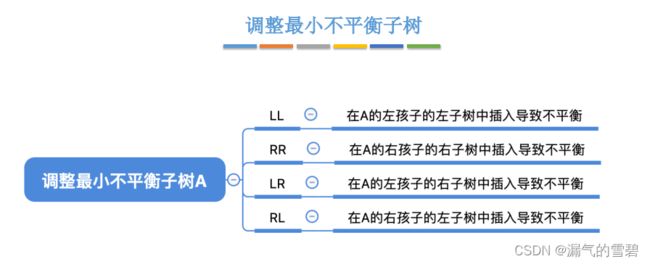
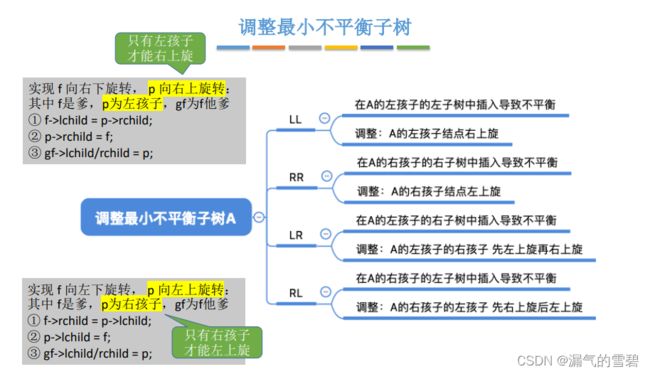
3.调整最小不平衡子树A
- 根据新结点插入位置的不同,分成下面四种情况:
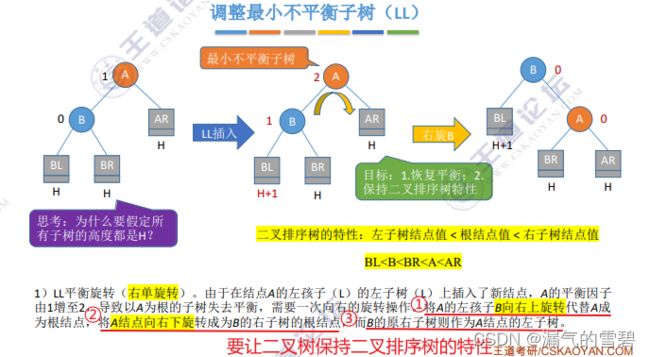
1)LL
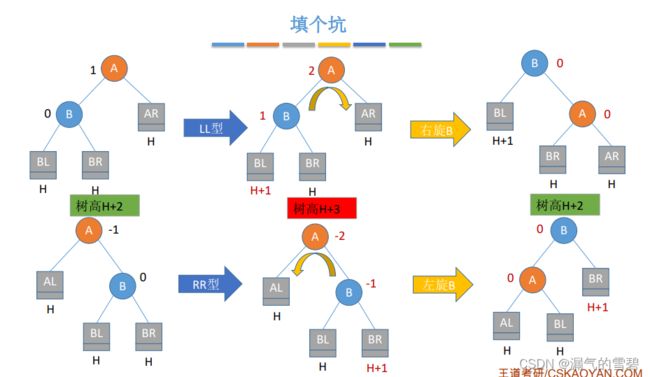
- 本小结中的A,我们设定是当插入新结点导致不平衡,A就刚好是不平衡子树的根结点,也就是第一个不平衡结点
- 下面分析下下图中的思考题:为什么要假定所有子树(AR,BL,BR)的高度都是H?
- ① 如果AR为H+1,当BL插入新结点时,A = (H+2) - (H+1) = 1,仍平衡,矛盾
- ② 如果BR为H-1,此时B = H -(H-1)= 1,BL再插入新结点,B=2,B变成了不平衡因子了
- 其他情况类似,所以只有当(AR,BL,BR)的高度都为H时,才会发生LL不平衡
- LL调整方法:
- 还是看图吧,解释太麻烦了
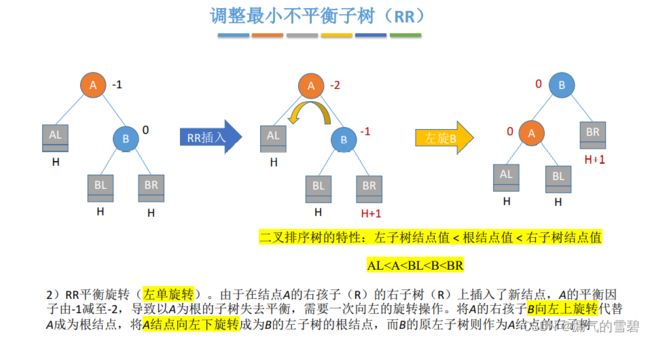
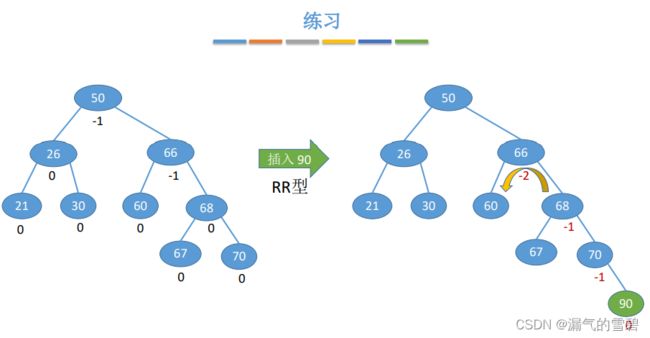
2)RR
- 在A的右孩子的右子树插入导致的不平衡
- LL和RR有点类似,可以搭配对比记忆
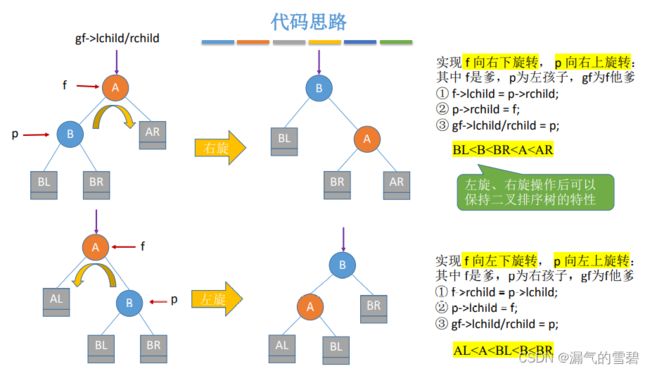
// LL情况
// 需要调整的指针:B->rChilde,A->lChild
// p孩子 f父亲 gf爷爷
// 注意下面代码顺序
f->lChild = p->rChild;
p->rchild = f;
pf->child = p;
// RR情况类似,自己看图
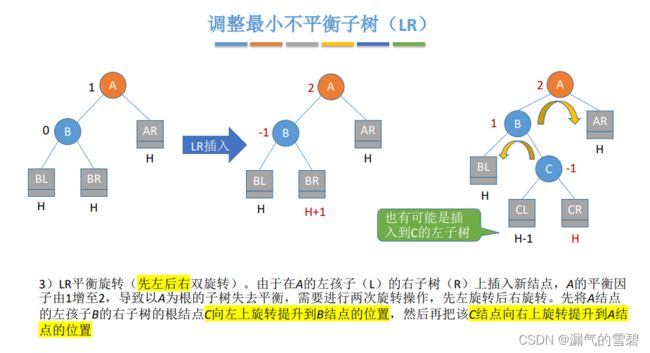
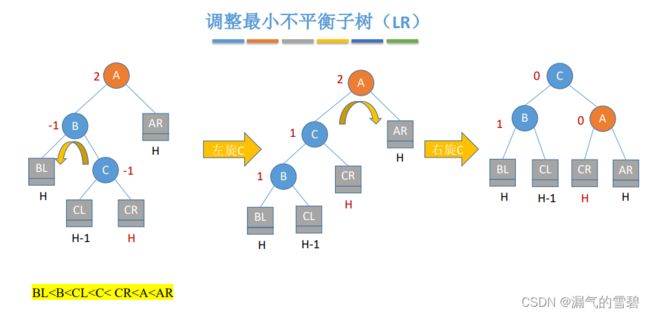
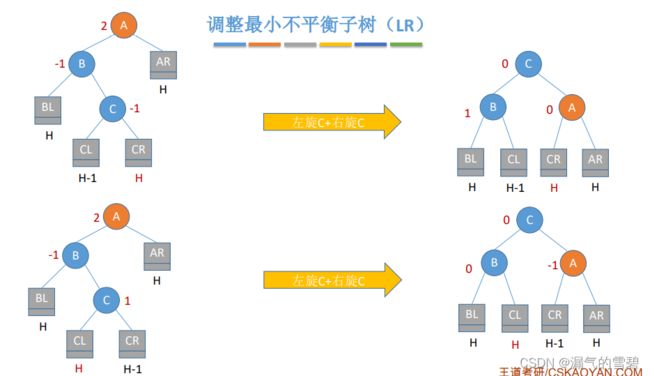
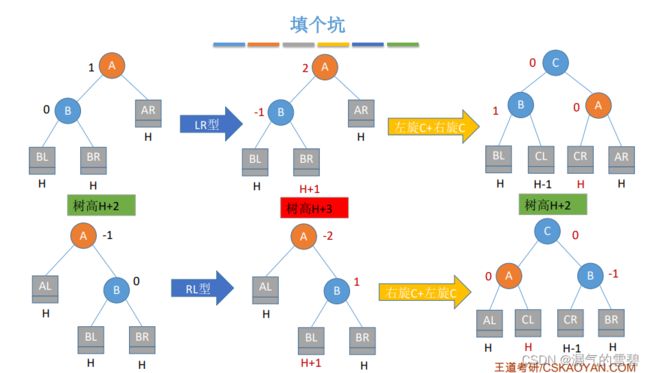
3)LR
- 在A的左孩子的右子树中插入新结点导致不平衡
- 在C的左、右插入新结点,情况都一样
- 左旋 + 右旋
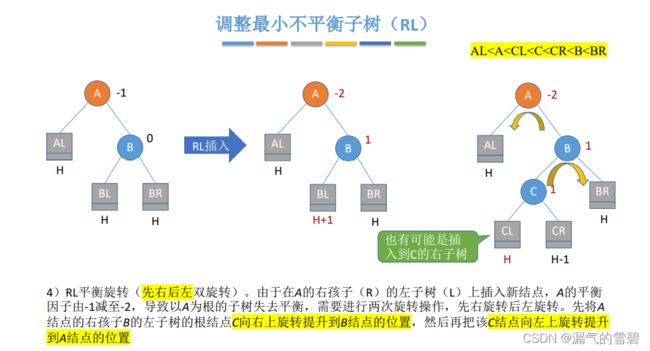
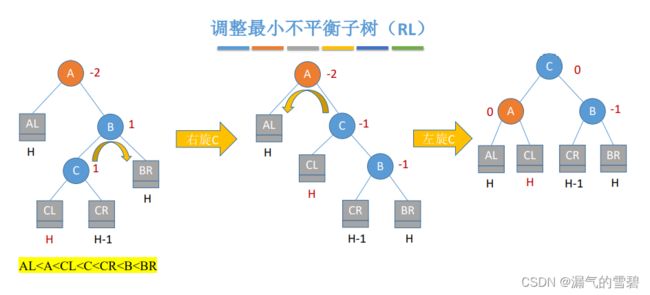
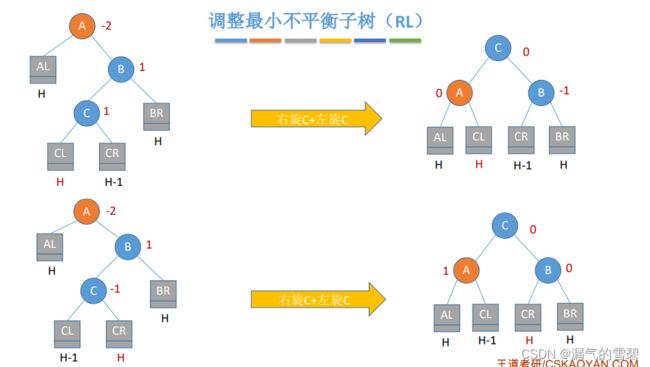
4)RL
- 在A的右孩子的左子树插入新结点导致不平衡
- 右旋 + 左旋
5)小小小结
- 只有左孩子才能右旋
- 只有右孩子才能左旋
6)扩展
- 解释:为什么只要处理最小不平衡子树,整棵二叉树就都平衡了?
- 举例论证
- 结论:插入操作导致“最小不平衡子树的高度+1”,经过平衡处理之后高度恢复
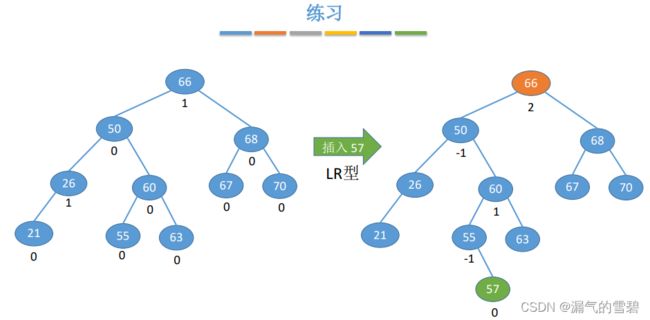
7)练习
- ①
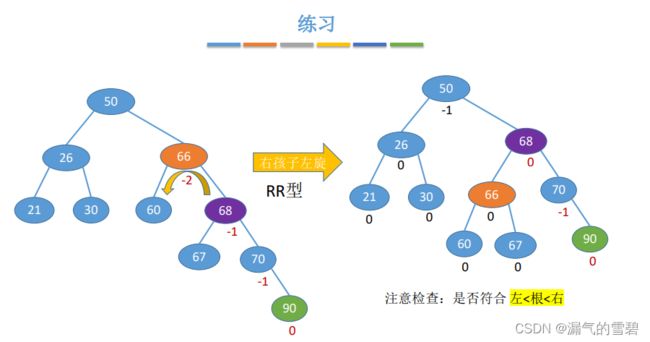
- ②
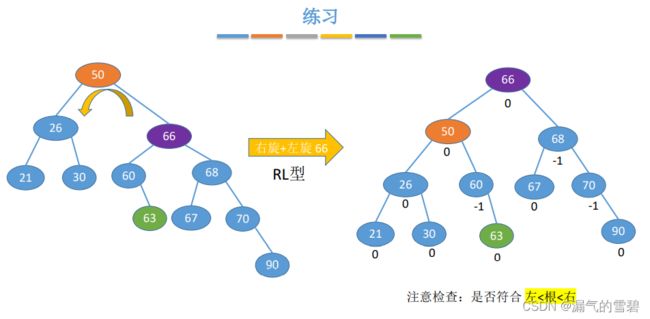
- ③
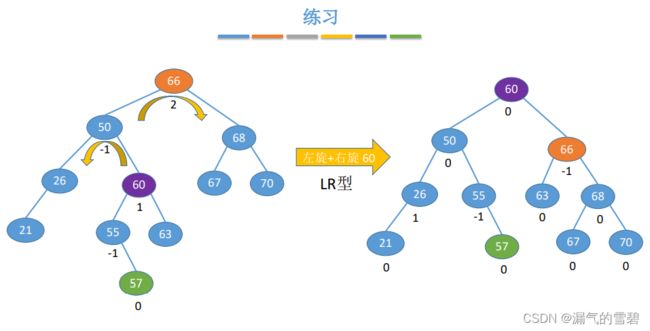
- 做熟练的话就不需要每次都选择去得到平衡二叉树。
- 1、60的左子树 --> 50的右子树
- 2、60的右子树 --> 66的左子树
- 3、60充当根结点,连接50和66(记得把55和66之间的线断掉)
4.平衡二叉树的查找
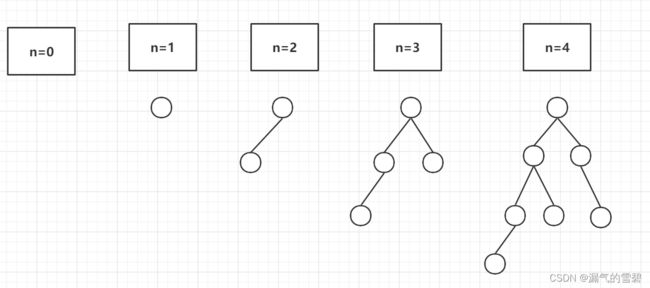
- 现在推导高h的平衡二叉树最小有几个结点:
| 高h | 最小结点数n |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 7 |
| h | n(h-1)+ n(h-2)+ 1 【下面两层加一】 |
- 一定要记住平衡二叉树最小结点数的递推式
- 通过n(h)的表达式,我们可以得到平衡二叉树的最大深度、树高
5.小结
5.5.3 哈夫曼树
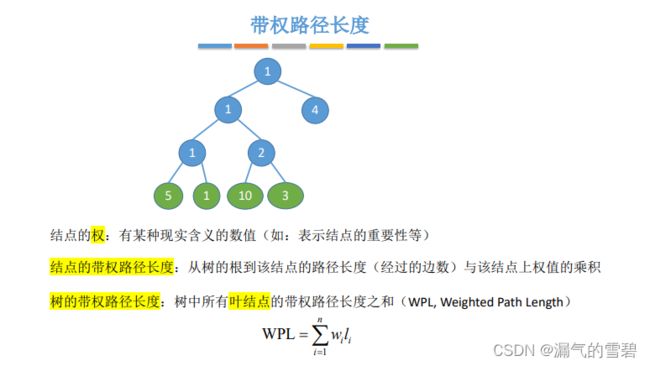
1.带权路径长度
- 结点的权:结点里有个权值属性
- 结点的带权路径长度:从根结点到该结点的路径长度 * 权值
- 树的带权路径长度:所有叶结点的带权路径长度之和(注意!!!只算叶子结点)
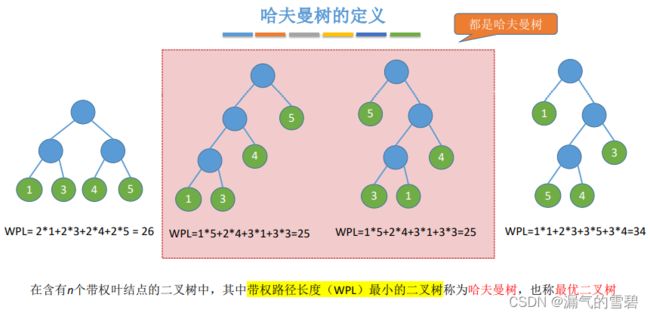
2.定义
- 哈夫曼树:带权路径长度(WPL)最小的二叉树
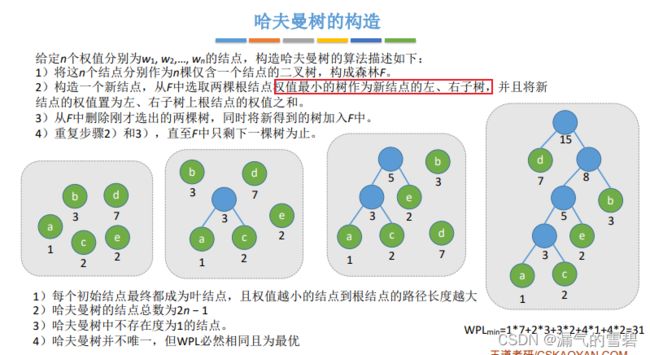
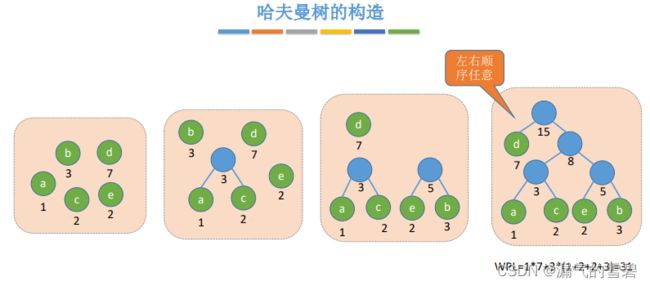
3.构造
- 构造哈夫曼树的步骤:
- 1、选权值最小的两个结点
- 2、在剩下的结点中挑一个最小的结点继续结合;或者挑两个结点先结合
- 哈夫曼树的一些性质:
- ① 结点总数为2 * n -1
- ② 不存在度为1的结点
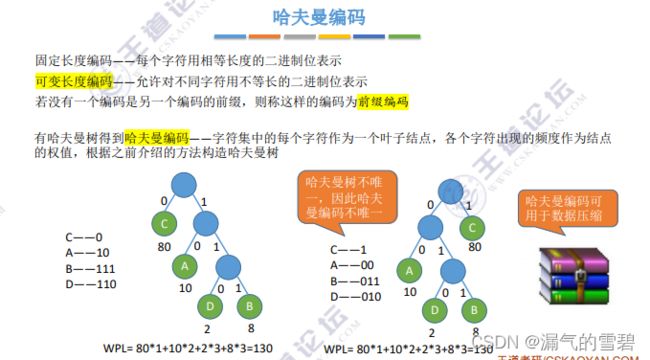
- ③ 哈夫曼树不唯一
- n个带权的叶子结点 可以 构造出多种不同形态的哈夫曼树
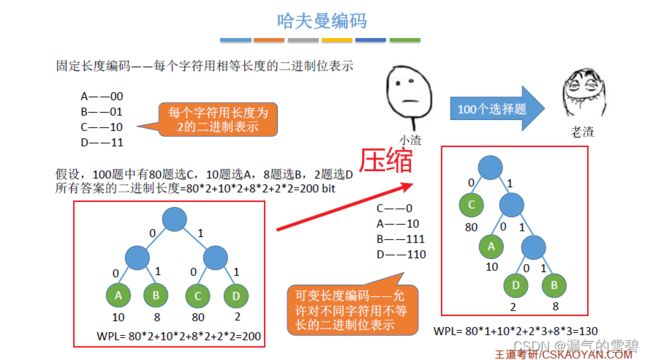
4.举例
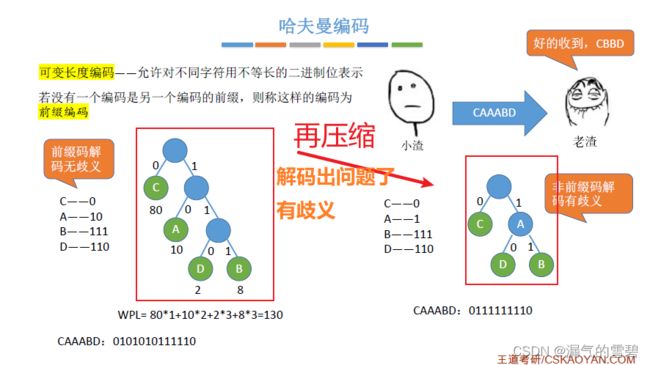
- 使用哈夫曼编码,减少发生二进制位长度
- 再一次压缩,解码出问题了,有歧义
5.小结
考研人加油!!!