JavaScript实现数据结构与算法(四)树结构
JavaScript实现数据结构与算法(四)树结构
-
- (四)树结构
-
- 1. 树的相关概念
-
- 1.1 树的基本概念
-
- 1.1.1 树结构的优势
- 1.1.2 树的术语
- 1.1.3 树的表示方法
- 1.2 二叉树
-
- 1.2.1 二叉树的概念
- 1.2.2 二叉树的定义
- 1.2.3 二叉树的五种形态
- 1.2.4 二叉树的特性
- 1.2.5 特殊二叉树
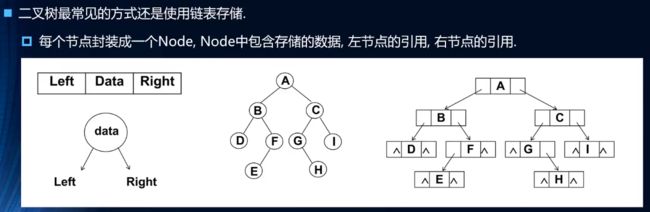
- 1.2.6 二叉树的存储
- 2. 二叉搜索树(BST)
-
- 2.1 概念
-
- 2.1.1 定义
- 2.1.2 特点
- 2.1.3 优势
- 2.1.4 缺陷
- 2.1.5 非平衡树
- 2.2 代码封装
-
- 2.2.1 代码解析
- 2.2.2 常见操作
- 2.2.3 封装二叉树代码实现
- 3. 树的遍历
-
- 3.1 先序遍历
-
- 3.1.1 遍历顺序
- 3.1.2 代码实现
- 3.1.3 测试代码
- 3.2 中序遍历
-
- 3.2.1 遍历顺序
- 3.2.2 代码实现
- 3.2.3 测试代码
- 3.3 后序遍历
-
- 3.3.1 遍历顺序
- 3.3.2 代码实现
- 3.3.3 测试代码
- 4. 二叉搜索树
-
- 4.1 最大值最小值
-
- 4.1.1 解析
- 4.1.2 代码实现
- 4.1.3 测试代码
- 4.2 查找特定的值
-
- 4.2.1 代码解析
- 4.2.2 代码实现
- 4.2.3 代码测试
- 4.3 删除节点
-
- 4.3.1 概念解析
- 4.3.2 代码实现
- 4.3.3 测试代码
- 5. 树的平衡性
-
- 5.1 定义
- 5.2 常见的平衡树
-
- 5.2.1 AVL树
- 5.2.2 红黑树
- 6. 红黑树
-
- 6.1 规则
- 6.2 相对平衡
- 6.3 变换
-
- 6.3.1 变色
- 6.3.2 旋转
- 6.3.3 插入操作
-
- 6.3.3.1 插入分析
- 6.3.3.2 红黑树插入案例
(四)树结构
学习笔记:coderwhy的JavaScript实现数据结构与算法的课程
其他章节笔记链接
1. 重要性
2. 线性结构
3. 哈希表
4. 树结构【本文】
5. 图结构
6. 排序和搜索
1. 树的相关概念
1.1 树的基本概念
1.1.1 树结构的优势
1.1.2 树的术语

节点的度、树的度、叶节点、父节点、子节点、兄弟节点、路径和路劲长度

1.1.3 树的表示方法
(1)普通表示方法
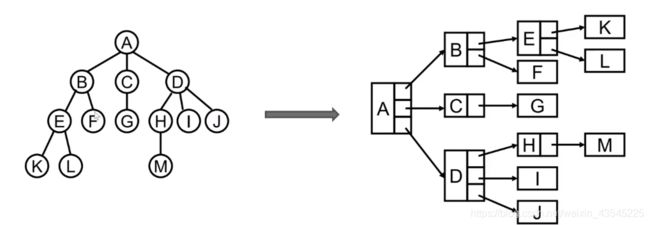
(2)儿子兄弟表示方法
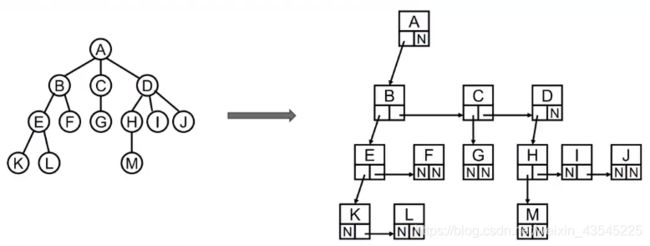
(3)儿子兄弟表示方法的旋转
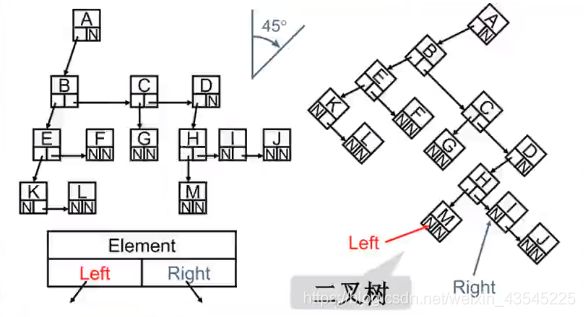
1.2 二叉树
1.2.1 二叉树的概念
1.2.2 二叉树的定义
1.2.3 二叉树的五种形态
1.2.4 二叉树的特性
1.2.5 特殊二叉树
1.2.6 二叉树的存储
2. 二叉搜索树(BST)
2.1 概念
2.1.1 定义
2.1.2 特点
2.1.3 优势
2.1.4 缺陷
2.1.5 非平衡树
2.2 代码封装
2.2.1 代码解析
2.2.2 常见操作
2.2.3 封装二叉树代码实现
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>二叉搜索树</title>
</head>
<body>
<script>
// 封装二叉搜索树
function BinarySearchTree(){
// 封装内部类
function Node(key) {
this.key = key;
this.left = null;
this.right = null;
};
// 属性
this.root = null;
// 方法
// 插入数据:对外给用户调用的方法
BinarySearchTree.prototype.insert = function (key) {
// 1. 根据key创建节点
var newNode = new Node(key);
// 2. 判断根节点是否有值
if (this.root == null){
this.root = newNode;
}else{
this.insertNode(this.root, newNode);
};
};
BinarySearchTree.prototype.insertNode = function (node, newNode) {
if(newNode.key < node.key){ // 向左查找
if(node.left == null){
node.left = newNode;
}else{
this.insertNode(node.left,newNode);
}
}else{ // 向右查找
if (node.right == null){
node.right = newNode;
}else{
this.insertNode(node.right,newNode);
}
}
};
};
// 测试代码
// 1. 创建BinarySearchTree
var bst = new BinarySearchTree();
// 2. 插入数据
bst.insert(11);
bst.insert(7);
bst.insert(15);
bst.insert(5);
bst.insert(3);
bst.insert(9);
bst.insert(8);
bst.insert(10);
bst.insert(13);
bst.insert(12);
bst.insert(14);
bst.insert(20);
bst.insert(18);
bst.insert(25);
bst.insert(6);
</script>
</body>
</html>
3. 树的遍历
3.1 先序遍历
3.1.1 遍历顺序
3.1.2 代码实现
// 树的遍历
// 1. 先序遍历
BinarySearchTree.prototype.preOrderTraversal = function (handler) {
this.preOrderTraversalNode(this.root,handler);
};
BinarySearchTree.prototype.preOrderTraversalNode = function (node,handler) {
if (node != null){
// 1. 查找经过的节点
handler(node.key);
// 2. 查找经过节点的左子节点
this.preOrderTraversalNode(node.left,handler);
// 3. 查找经过节点的右子节点
this.preOrderTraversalNode(node.right,handler);
}
};
3.1.3 测试代码
var resultString = "";
bst.preOrderTraversal(function (key) {
resultString += key + " "
});
alert(resultString);
3.2 中序遍历
3.2.1 遍历顺序
3.2.2 代码实现
// 2. 中序遍历
BinarySearchTree.prototype.midOrderTraversal = function (handler) {
this.midOrderTraversalNode(this.root,handler);
};
BinarySearchTree.prototype.midOrderTraversalNode = function (node,handler) {
if (node != null){
// 1. 查找左子树中的节点
this.midOrderTraversalNode(node.left,handler);
// 2. 查找经过的节点
handler(node.key);
// 3. 查找右子树中节点
this.midOrderTraversalNode(node.right,handler);
}
};
3.2.3 测试代码
var resultString = "";
bst.midOrderTraversal(function (key) {
resultString += key + " "
});
alert(resultString);
3.3 后序遍历
3.3.1 遍历顺序
3.3.2 代码实现
BinarySearchTree.prototype.postOrderTraversal = function (handler) {
this.postOrderTraversalNode(this.root,handler);
};
BinarySearchTree.prototype.postOrderTraversalNode = function (node,handler) {
if (node != null){
// 1. 查找左子树中的节点
this.postOrderTraversalNode(node.left,handler);
// 2. 查找右子树中节点
this.postOrderTraversalNode(node.right,handler);
// 3. 查找经过的节点
handler(node.key);
}
};
3.3.3 测试代码
var resultString = "";
bst.postOrderTraversal(function (key) {
resultString += key + " "
});
alert(resultString);
4. 二叉搜索树
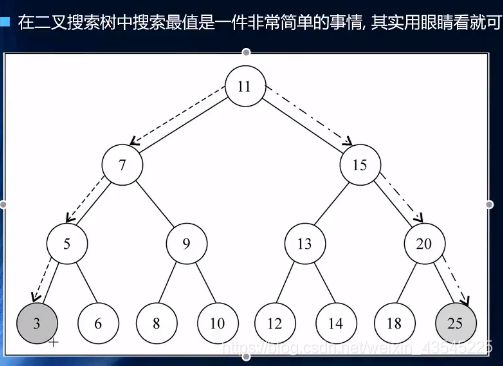
4.1 最大值最小值
4.1.1 解析
4.1.2 代码实现
// 寻找最值
BinarySearchTree.prototype.max = function () {
// 1. 获取根节点
var node = this.root;
// 2. 依次向右不断的查找,直到节点为null
var key = null;
while (node != null){
key = node.key;
node = node.right;
}
return key;
};
BinarySearchTree.prototype.min = function () {
// 1. 获取根节点
var node = this.root;
// 2. 依次向左不断的查找,直到节点为null
var key = null;
while (node != null){
key = node.key;
node = node.left;
}
return key;
};
4.1.3 测试代码
alert(bst.max());
alert(bst.min());
4.2 查找特定的值
4.2.1 代码解析
4.2.2 代码实现
// 搜索某一个key
BinarySearchTree.prototype.search = function (key) {
// 1. 获取根节点
var node = this.root;
// 2. 循环搜索key
while(node!=null){
if (node.key == key){
return true;
} else if(node.key > key ){
node = node.left;
}else{
node = node.right;
};
};
return false;
};
4.2.3 代码测试
alert(bst.search(25));
alert(bst.search(24));
alert(bst.search(2));
4.3 删除节点
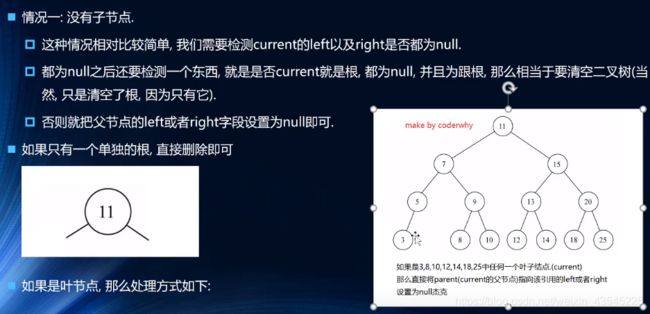
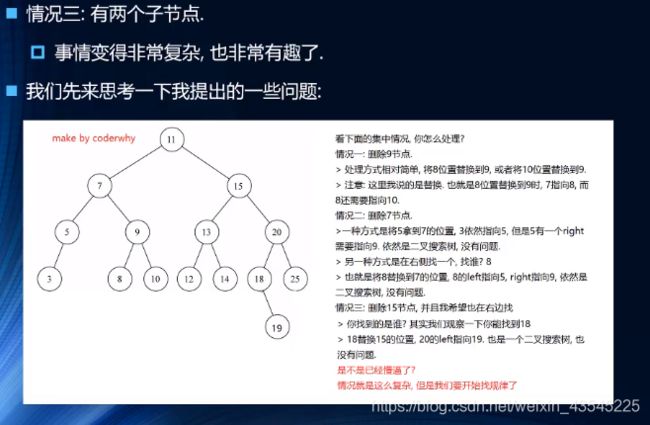
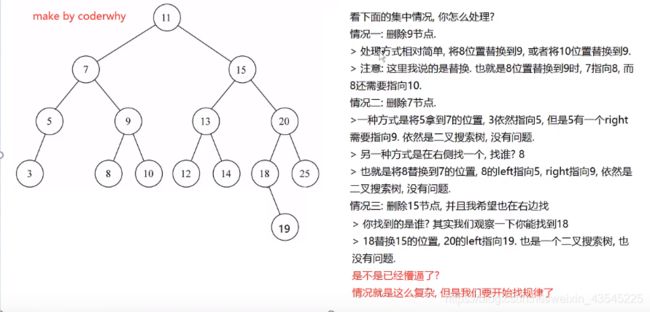
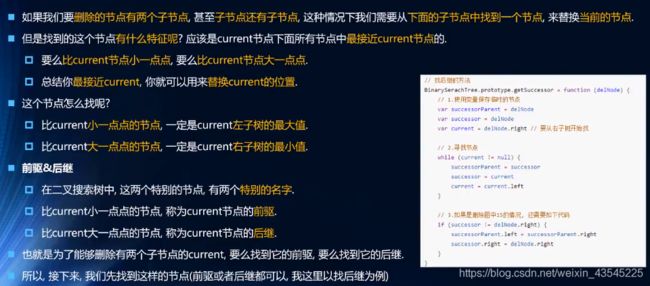
4.3.1 概念解析
4.3.2 代码实现
// 删除节点
BinarySearchTree.prototype.remove = function (key) {
// 1. 寻找要删除的节点
// // 先判断树中是否有该值
// if (!this.search(key)){
// return false;
// }
// 1.1 定义变量,保存一些信息
var current = this.root;
var parent = null;
var isLeftChild = true; // 判断向左寻找的标志
// 1.2 开始寻找删除的节点
while (current.key != key) {
parent = current;
if (key < current.key) {
isLeftChild = true;
current = current.left;
} else {
isLeftChild = false;
current = current.right;
}
if (current == null) {
return false;
}
}
;
// 2. 根据对应的盈眶删除节点
// 找到了current==key
// 2.1 删除的节点是叶子节点(没有子节点)
if (current.left == null && current.right == null) {
if (current == this.root) {
this.root = null;
} else {
if (isLeftChild) {
parent.left = null;
} else {
parent.right = null;
}
;
}
;
}
// 2.2 删除的节点有一个子节点
else if (current.right == null) {
if (current == this.root) {
this.root = left;
} else if (isLeftChild) {
parent.left = current.left;
} else {
parent.right = current.left;
}
;
} else if (current.left == null) {
if (current == this.root) {
this.root = right;
} else if (isLeftChild) {
parent.left = current.right;
} else {
parent.right = current.right;
}
}
// 2.3 删除的节点有两个子节点
else{
// 1. 获取后继节点
var succssor = this.getSuccssor(current);
// 2. 判断是否是根节点
if (current == this.root){
this.root = succssor;
}else if (isLeftChild) {
parent.left = succssor;
}else{
parent.right = succssor;
};
// 3. 将删除节点的左子树 = current.left
succssor.left = current.left;
}
;
};
// 找后继的方法
BinarySearchTree.prototype.getSuccssor = function (delNode) {
// 1. 定义变量,保存找到的后继
var succssor = delNode;
var current = delNode.right;
var succssorParent = delNode;
// 2. 循环查找
while (current != null){
succssorParent = succssor;
succssor = current;
current = current.left;
}
// 3. 判断寻找到的后继节点是否就是delNode的right节点
if (succssor != delNode.right){
succssorParent.left = succssor.right;
succssor.right = delNode.right;
}
return succssor;
}
4.3.3 测试代码
bst.remove(9);
bst.remove(7);
bst.remove(15);
var resultString = "";
bst.preOrderTraversal(function (key) {
resultString += key + " "
});
alert(resultString);
5. 树的平衡性
5.1 定义
5.2 常见的平衡树
5.2.1 AVL树
5.2.2 红黑树
6. 红黑树
6.1 规则
6.2 相对平衡
6.3 变换
6.3.1 变色
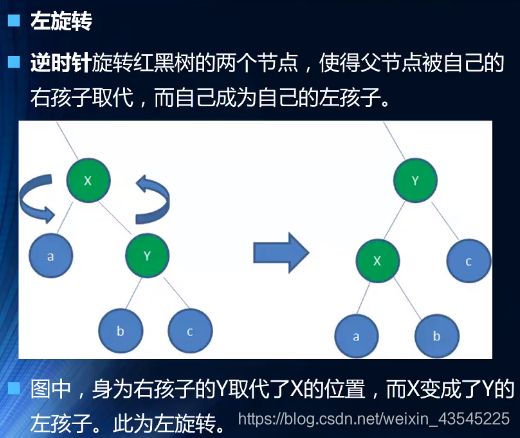
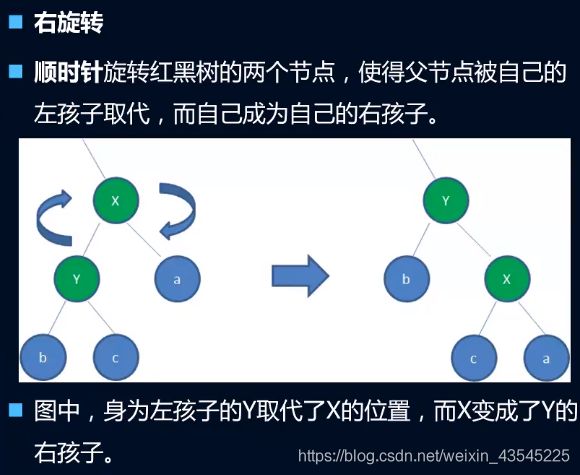
6.3.2 旋转
6.3.3 插入操作
6.3.3.1 插入分析

插入的节点默认是红色


(1)情况一:

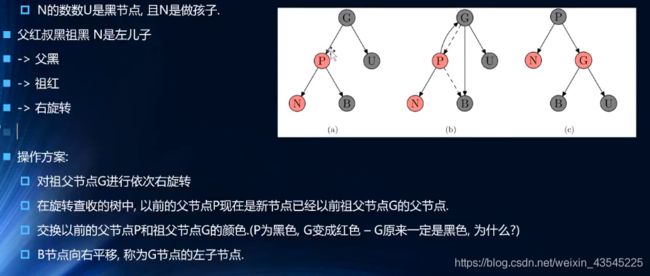
(2)情况二:

(3)情况三:
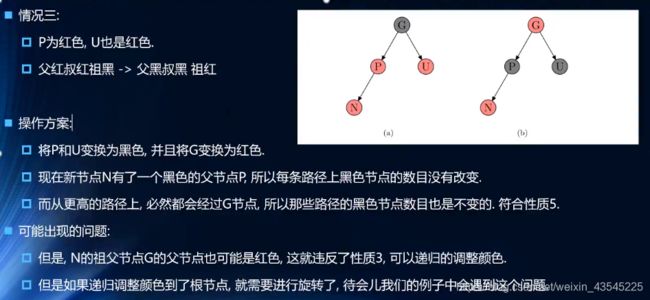
(4)情况四:
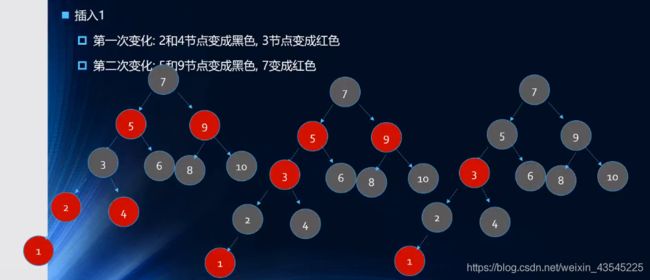
6.3.3.2 红黑树插入案例
插入:10 9 8 7 6 5 4 3 2 1

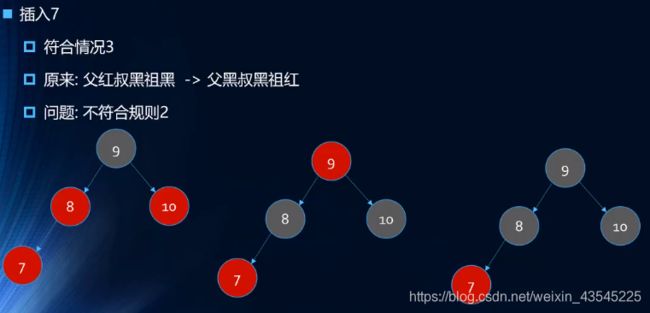
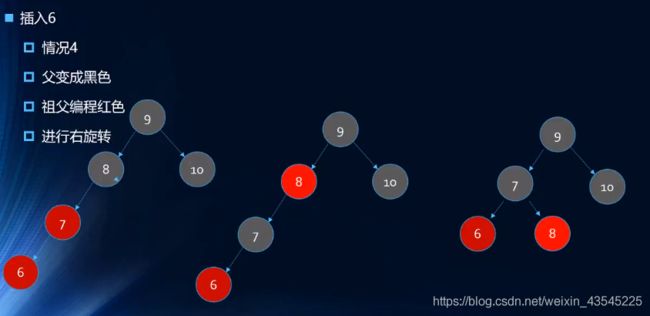
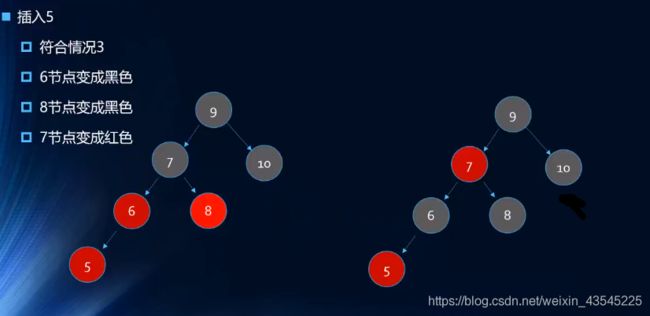

![]()

—————————————————————————————————————————
如果我的文章能帮你节约20秒,就请你为我的文章点个赞吧!