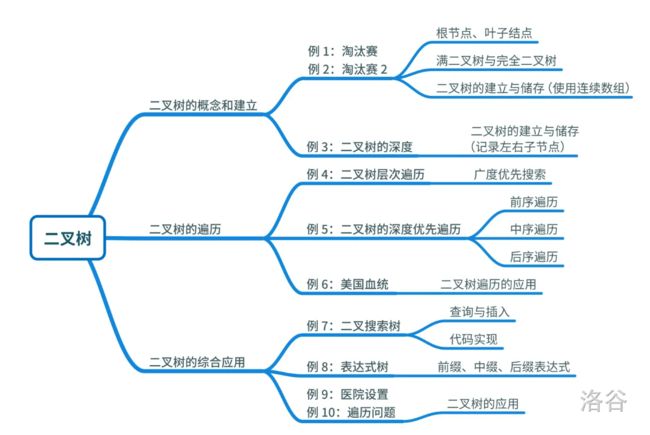
【洛谷二叉树】

【数据结构1-2】二叉树 - 题单 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

就是一个而二叉树洛谷官方题单

并没有写完，还差两道题，但是已经急着来写了QwQ（感觉那两题太难就润了

主要考察的是

二叉树的：

概念

性质

存储结构

遍历

总之就是很基础很简单的题

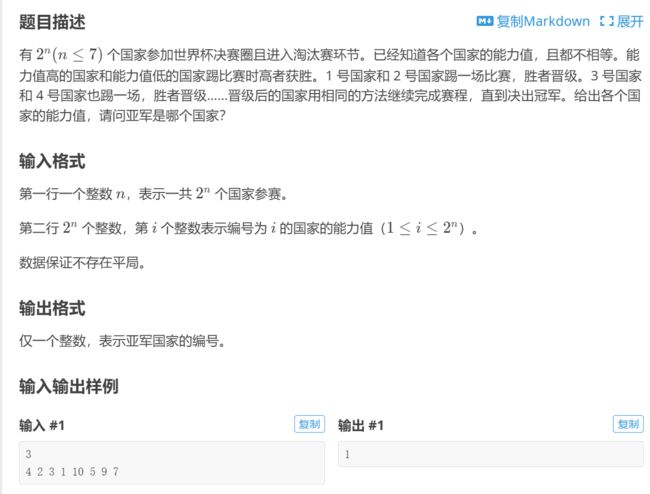
一、P4715 【深基16.例1】淘汰赛

P4715 【深基16.例1】淘汰赛 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

考的是已知二叉树最底层，怎么建树

其实这个就是线段树的build

#include 
using namespace std;
#define int long long
const int mxn=2e2+10;
map mp;
int n;
int a[mxn],tree[mxn<<1];
void pushup(int rt){
    tree[rt]=max(tree[rt<<1],tree[rt<<1|1]);
}
void build(int rt,int l,int r){
    if(l==r){
        tree[rt]=a[l];
        return;
    }
    int mid=l+r>>1;
    build(rt<<1,l,mid);
    build(rt<<1|1,mid+1,r);
    pushup(rt);
}
void solve(){
    cin>>n;
    for(int i=1;i<=(1<>a[i],mp[a[i]]=i;
    build(1,1,1<>__;
    while(__--)solve();return 0;
}

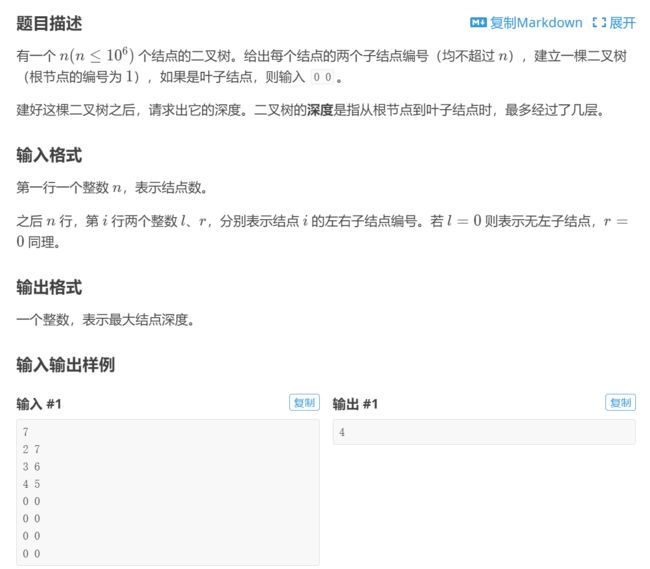
二、P4913 【深基16.例3】二叉树深度

P4913 【深基16.例3】二叉树深度 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

考的是二叉树怎么存储，一般用结构体存二叉树，就和线段树那种差不多，这样建的好处在于你可以递归建树

#include 
using namespace std;
const int mxe=1e6+10,mxn=1e6+10;
struct ty{
    int l,r;
}tree[mxe<<1];
int n;
int u,v,ans;
int vis[mxn];
void dfs(int u,int fa,int dep){
    ans=max(ans,dep);
    if(!vis[tree[u].l]&&tree[u].l!=0) vis[tree[u].l]=1,dfs(tree[u].l,u,dep+1);
    if(!vis[tree[u].r]&&tree[u].r!=0) vis[tree[u].r]=1,dfs(tree[u].r,u,dep+1);
}
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>u>>v;
        tree[i].l=u;
        tree[i].r=v;
    }
    dfs(1,-1,1);
    cout<

三、P1827 [USACO3.4] 美国血统 American Heritage

P1827 [USACO3.4] 美国血统 American Heritage - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

典中典之二叉树的遍历顺序问题

已知中序和前序或中序和后序，求另外一个直接递归就好了

#include 
using namespace std;
void dfs(int x1,int y1,int x2,int y2);
string p1,p2;
int main(){
    cin>>p1>>p2;
    dfs(0,p1.length()-1,0,p2.length()-1);
    return 0;
}
void dfs(int x1,int y1,int x2,int y2){
    if(x1>y1||x2>y2) return;
    else{
        char x=p2[x2];
    for(int i=0;i

四、P1229 遍历问题

P1229 遍历问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

考的是二叉树遍历的不确定性

首先是一个结论：给定二叉树的前序和后序遍历，其中序遍历是不确定的，只有一个儿子结点的结点会影响确定性

充分性的原因是，如果一个结点只有一个儿子结点，那么这个儿子结点可以作为左结点，也可以作为右结点，而无论是左还是右，在前序遍历和后序遍历中的结果是一样的，但是在中序遍历中不一样

必要性的原因可以用反证法：假设一个结点有两个儿子结点

那么前序遍历是：根左右

后序遍历是：左右根

根确定，左的长度确定，这样就是一一对应过去，所以右也确定了

记只有一个儿子的结点有ans个

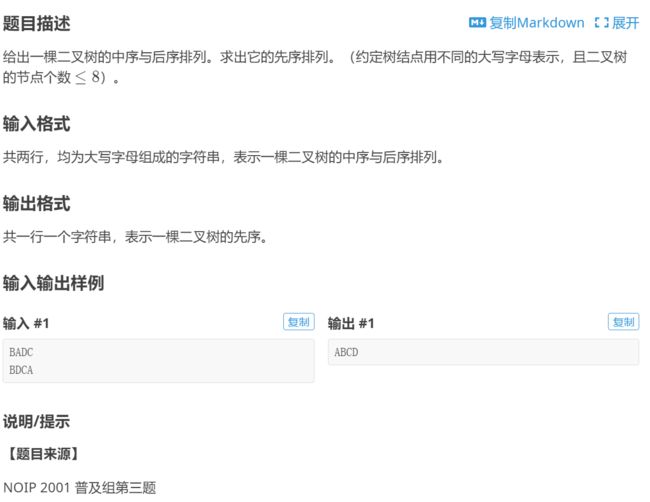
然后给定前序和后序，中序有(1<

#include 
using namespace std;
const int mxe=2e5+10,mxn=5e5+10;
string s1,s2;
void solve(){
    cin>>s1>>s2;
    int ans=0;
    for(int i=0;i>__;
    while(__--)solve();return 0;
}

五、P1030 [NOIP2001 普及组] 求先序排列

P1030 [NOIP2001 普及组] 求先序排列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

这个和前面那个是一样的道理

#include 
using namespace std;
string s1,s2;
int ansi;
void dfs(int l1,int r1,int l2,int r2){
    if(l1>r1||l2>r2) return;
    for(int i=0;i>s1>>s2;
    dfs(0,s1.size()-1,0,s2.size()-1);
}

六、P3884 [JLOI2009]二叉树问题

P3884 [JLOI2009]二叉树问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

树上前缀和裸题，直接上板子即可

#include 
using namespace std;
const int mxe=1e6+10,mxn=1e6+10;
struct ty{
    int to,next;
}edge[mxe<<1];
map mp;
queue q;
int n,u,v,rt,tot=0,a,b,mxdep=-1;
int head[mxn],vis[mxn],dep[mxn],f[mxn][65];
void add(int u,int v){
    edge[tot].to=v;
    edge[tot].next=head[u];
    head[u]=tot++;
}
void init(){
    tot=0;
    for(int i=0;i<=n;i++){
        head[i]=-1;
    }
}
void bfs(){
    memset(dep,0x3f,sizeof(dep));
    memset(vis,0,sizeof(vis));
    dep[0]=0,dep[1]=1;
    q.push(1),vis[1]=1;
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int i=head[u];~i;i=edge[i].next){
            if(vis[edge[i].to]) continue;
            vis[edge[i].to]=1;
            dep[edge[i].to]=dep[u]+1;
            q.push(edge[i].to);
            f[edge[i].to][0]=u;
            for(int j=1;j<=30;j++){
                f[edge[i].to][j]=f[f[edge[i].to][j-1]][j-1];
            }
        }
    }
}
int lca(int u,int v){
    if(dep[u]=0;k--){
        if(dep[f[u][k]]>=dep[v]){
            u=f[u][k];
        }
    }
    if(u==v) return u;
    for(int k=30;k>=0;k--){
        if(f[u][k]!=f[v][k]){
            u=f[u][k];
            v=f[v][k];
        }
    }
    return f[u][0];
}
void solve(){
    cin>>n;
    init();
    for(int i=1;i<=n-1;i++){
        cin>>u>>v;
        add(u,v);
        add(v,u);
    }
    bfs();
    int mx=-1;
    for(int i=1;i<=n;i++){
        mx=max(mx,dep[i]);
        mp[dep[i]]++;
    }
    for(auto it:mp) mxdep=max(mxdep,it.second);
    cout<>a>>b;
    cout<<(dep[a]-dep[lca(a,b)])*2+dep[b]-dep[lca(a,b)]<<'\n';
}
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int __=1;//cin>>__;
    while(__--)solve();return 0;
}

再加一题：(61条消息) 【二叉树】L2-006 树的遍历_lamentropetion的博客-CSDN博客