【蓝桥系列】——十三届蓝桥杯PythonB组第五题E题蜂巢（AC代码）
大家好，我是普通小明，初入学习博客，一起加油！
首先，感谢 小蓝刷题 对我的鼓励，我也希望加入学习算法这个大家庭。
第一篇文章，有些不完美，还请多多指教。
目录 （好像我并不会用锚点T-T）
省赛心得
蜂巢题解-思路点拨
蜂巢题解-AC代码
蜂巢题解-刷题总结
未来展望
省赛心得
遗憾落幕十三届蓝桥PyB省赛，破灭了大一自学算法拿下国奖的传奇神话
究其原因
1、对算法过多理论而缺少实践，缺少刷题量。
2、对算法的理解不够全面。
3、对数论算法有所欠缺。
立志
1、一年时间完成蓝桥刷题系统过半题量。
2、全面掌握各种算法，并且形成模板记忆。
3、多看数学难题，提升思维转换能力。
一、蜂巢题解-思路点拨
个人主页有另一个更简单的解法
读完题没思路怎么办？——模拟样例，模拟例子
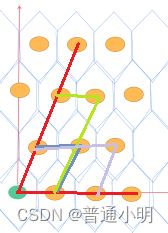
由对称关系不难得出，以绿点为起点，选任一橙点为终点既包含了所有两点之间距离的情况
先任选一个为终点
图1
如图1有六条路线最短，为了方便观察显然选取任意平行四边形一侧边为个体。
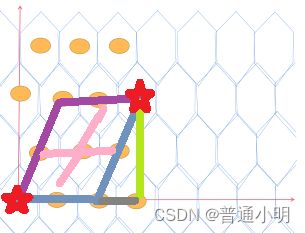
最短路总结多观察几个图形发现在对方节点所在方向（六边形六个方向）延长线所形成的交点都是最短路如图2和3
图2 图3
通过所有外围的节点进行最短路总结如图2如图3我们发现都是平行四边形
从而我们分析如何算平行四边形的一侧边距离（因为对称任选一侧都相等）就能得出最短路
再如图2和3不难发现图中有两种情况的平行四边形
情况1、先选蓝线右下方任一点分析如图4发现通过水平方向和竖直方向距离以及角度关系就能算出距离
图4
设x，y分别为水平、垂直距离，则蓝线距离为len=
情况2、再选蓝线左上方一点分析如图5发现无法由情况1算出，但我们知道是根据x，y两个距离算出的，我们先画出，发现紫线距离能转换成绿线距离。
图5
而绿线距离len=
设计坐标系，为了方便计算我们假设一个六边形的变长是
，所以水平方向上相邻两个橙点的距离就是2,因此最短路距离就是len//2
所以我们需要根据6个方向进行坐标映射——输入方向和距离，返回dx，dy两个增量
用e代表
def cc(f,len): # 坐标映射|| f为方向，len为行走的距离，返回值为dx，dy的增量（微分）
if f==0:return (-len,0)
elif f==1:return (-len/2,len*e/2)
elif f==2:return (len/2,len*e/2)
elif f==3:return (len,0)
elif f==4:return (len/2,-len*e/2)
elif f==5:return (-len/2,-len*e/2)最后根据len得出距离
# 蓝线可根据斜率区分，蓝线上的情况两种都可以所以这里分给蓝线右下方
if abs(y/x)<=e: # 蓝线右下方
len=round(((x-y*e/3)+(y*e*2/3))/2) # 因为根号有精度问题需要四舍五入
print("%d"%len)
else: # 蓝线左上方
len=round(y*e/3)
print("%d"%len)二、蜂巢题解-AC代码
def cc(f,len): # 坐标映射|| f为方向，len为行走的距离，返回值为dx，dy的增量（微分）
if f==0:return (-len,0)
elif f==1:return (-len/2,len*e/2)
elif f==2:return (len/2,len*e/2)
elif f==3:return (len,0)
elif f==4:return (len/2,-len*e/2)
elif f==5:return (-len/2,-len*e/2)
e=3**0.5 # 存根号3
d1,p1,q1,d2,p2,q2=map(int,input().split())
a1=[[d1,p1],[(d1+2)%6,q1]] # a路径的两次方向变化
b1=[[d2,p2],[(d2+2)%6,q2]] # b路径的两次方向变化
a=[0,0] # a点映射后的坐标（x，y）
b=[0,0] # b点映射后的坐标（x，y）
for i in range(2): # 进行a路径的坐标映射
dx,dy=cc(a1[i][0],a1[i][1]*2) # 因为一格长度是2所以*2
a[0]+=dx
a[1]+=dy
for i in range(2): # 进行b路径的坐标映射
dx,dy=cc(b1[i][0],b1[i][1]*2)
b[0]+=dx
b[1]+=dy
x,y=abs(b[0]-a[0]),abs(b[1]-a[1]) # 计算a点b点的水平垂直距离
# 蓝线可根据斜率区分，蓝线上的情况两种都可以所以这里分给蓝线右下方
if abs(y/x)<=e: # 蓝线右下方
len=round(((x-y*e/3)+(y*e*2/3))/2) # 因为有根号有精度问题需要进行四舍五入
print("%d"%len)
else: # 蓝线左上方
len=round(y*e/3)
print("%d"%len)
三、蜂巢题解-刷题总结
1、首先读题，为了补充思路可以先模拟样例，再进行各种情况的模拟
扩展到以后，读不懂题或无思路可进行5分钟左右的模拟寻找思路
2、掌握基本的坐标系，三角函数，几何问题等
四、未来展望
1、第一次写博客，可能有一些排版问题，也可能有讲解臃肿，还请各位同学指出我加以改正，能够写出更好的题解思路
2、作为二本大一，我本着以赛促学参加各种比赛，学习算法知识为考研也为进入大厂！很庆幸认识了 小蓝刷题 能一块努力，准备明年的比赛！
3、计划以ACM算法为标准进行系统的算法学习（可怜学校并无AMC队），并且在蓝桥刷题系统应用到实践上，让理论不止于理论，让本届比赛的遗憾成为过去。