第十三届蓝桥杯省赛python B组题解
文章目录
- A、排列字母
- B、寻找整数
- C、纸张尺寸
- D、数位排序
- E、蜂巢
- F、消除游戏
- G、全排列的价值
- H、技能升级
- I、最长不下降子序列
- J、最优清零方案
A、排列字母
a = 'WHERETHEREISAWILLTHEREISAWAY'
print(''.join(sorted(a)))
结果:
AAAEEEEEEHHHIIILLRRRSSTTWWWY
B、寻找整数
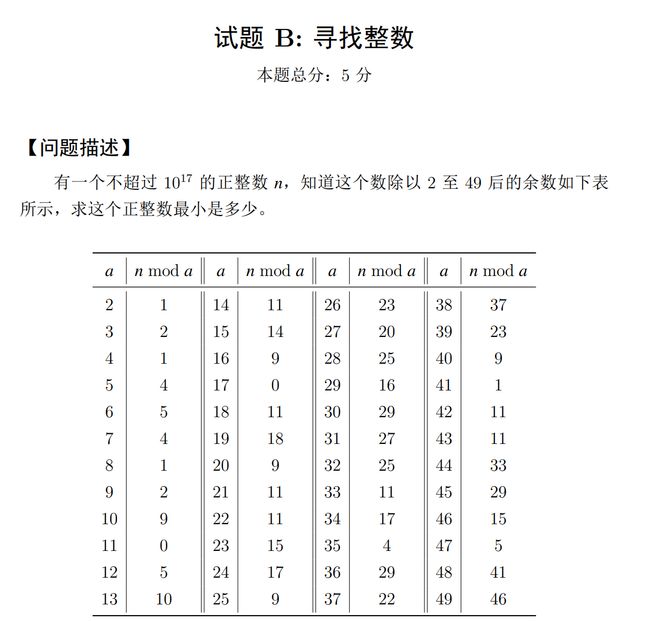
可以利用中国剩余定理拓展解题,我总结了一下,大家可以参考Link
C、纸张尺寸
a = input()
A0x = 1189
A0y = 841
k = int(a[1])
for i in range(k):
A0x,A0y = A0y,A0x//2
print(A0x)
print(A0y)
#(1189,841),(841,594),(594,420),(420,297),(297,210),(210,148),(148,105),(105,74),(74,52),(52,37)
D、数位排序
n = int(input())
m = int(input())
l = []
#求和数
def nums(x):
num = sum(list(map(int,list(str(x)))))
return num
for i in range(1,n+1):
b = nums(i)
l.append((b,i))
s = sorted(l) #默认元组(b,i)的第一位从小到大排序,其次按在列表l中的位置,前则前
print(s[m-1][1])
方法2、 利用cmp_to_key进行多条件比较求解
from functools import cmp_to_key
n = int(input())
m = int(input())
l = [i for i in range(1,n+1)]
def nums(x):
num = sum(list(map(int,list(str(x)))))
return num
def cmp(x,y):
a = nums(x)
b = nums(y)
if a==b:
return x-y #小于0,不变
return a-b
li = sorted(l,key=cmp_to_key(cmp))
print(li[m-1])
E、蜂巢
直接上 大佬题解
SQRT_3 = 3 ** 0.5
def dir_tran(direct):
''' direct: 方向
return: 单位步长的分量'''
if direct == 0:
x, y = -1, 0
elif direct == 1:
x, y = -1 / 2, SQRT_3 / 2
elif direct == 2:
x, y = 1 / 2, SQRT_3 / 2
else:
x, y = dir_tran(direct % 3)
x, y = -x, -y
return x, y
def loc_tran(d, p, q):
''' 将 (d, p, q) 坐标转换为 (x, y) 坐标'''
# 沿 d 方向走 p 步
x1, y1 = dir_tran(d)
x1, y1 = x1 * p, y1 * p
# 沿 (d+2)%6 方向走 q 步
x2, y2 = dir_tran((d + 2) % 6)
x2, y2 = x2 * q, y2 * q
return x1 + x2, y1 + y2
d1, p1, q1, d2, p2, q2 = map(int, input().split())
x1, y1 = loc_tran(d1, p1, q1)
x2, y2 = loc_tran(d2, p2, q2)
# 求出等价的距离向量
x, y = abs(x1 - x2), abs(y1 - y2)
# 回到 x 轴所需的步数
total_pace = y / SQRT_3 * 2
# 回到 x 轴时, 在 x 方向上产生的最大偏移量
x_move = y / SQRT_3
# 在 x 方向上还需移动的步数
total_pace += max([0, x - x_move])
print(int(round(total_pace)))
F、消除游戏
# 定义函数删除边缘字符
def qu(s):
a = []
i = 1
while i<len(s)-1:
if s[i-1]==s[i] and s[i]!=s[i+1]:
a.append(i)
a.append(i+1)
if s[i-1]!=s[i] and s[i]==s[i+1]:
a.append(i-1)
a.append(i)
i += 1
b = set(a)
s = list(s)
for i in b:
s[i]=''
return ''.join(s)
m = input()
# 进行2**64次操作
for i in range(2**64):
x = m
m = qu(x)
if x==m:
print(m)
break
if len(m)==0:
print('EMPTY')
break
G、全排列的价值
方法1、 暴力解法,但毫无疑问处理大数据会超时。
from itertools import permutations
n = int(input())
l = [i for i in range(1,n+1)]
def val(x):
a = 0
for i in range(len(x)):
for j in range(i):
if x[j]<x[i]:
a += 1
return a%998244353
num = 0
for p in permutations(l,n):
num += val(p)
print(num)
方法2、 将最大的数插入前面数的全排列,寻找规律,写出递推公式。
当输入 n=1 时,全排列价值为 0.
1
当输入 n=2 时,全排列价值为 1.
可以看作 2 插空 1 的全排列。1 * 1 + 0
1 2
2 1
当输入 n=3时,全排列价值为 (1 * 2)* (0+1+2) + 1 * 3 = 9.
可以看作 3 插空(1,2)的全排列。
3 1 2
1 3 2
1 2 3
3 2 1
2 3 1
2 1 3
当输入 n=4时,全排列价值为(1 * 2 * 3)*(0+1+2+3)+ 9 * 4 = 72.
可以看作 4 插空(1,2,3)的全排列。可以参照上面矩阵,将4从左到右插空。
仔细想一想,规律不难发现,这里就依照 n=4 说明。
(1 * 2 * 3)可表示为 (n-1)! 就是要进行插空操作的(1,2,3)全排列行数。
(0+1+2+3)可表示为 n *(n-1)/ 2,就是将最大值 4 从左到右插入四个空分别产生的价值数 。
9 * 4 可表示为 (n-1 全排列价值数) * n, 因为 (0 ~ n)的全排列个数就是(0 ~ n-1)全排列个数的 n 倍。(n-1 全排列价值数)就要增大 n 倍。
import math
n = int(input())
a = [0,1]
for i in range(3,n+1):
a.append((math.factorial(i-1) * (i*(i-1)//2) + a[i-2]*i) % 998244353)
print(a[i-1])
参考链接
方法3、 根据全排列的板子可以找出规律
(3, 2, 1) : 0 + 0 + 0 = 0 ;
(3, 1, 2) : 0 + 0 + 1 = 1 ;
(2, 1, 3) : 0 + 0 + 2 = 2 ;
(2, 3, 1) : 0 + 1 + 0 = 1 ;
(1, 3, 2) : 0 + 1 + 1 = 2 ;
(1, 2, 3) : 0 + 1 + 2 = 3 ;
⇓ 将 每 一 列 出 现 的 价 值 写 出 来 \Downarrow 将每一列出现的价值写出来 ⇓将每一列出现的价值写出来
0 0 0
1 1
2
而每一列重复出现的次数为**其余列元素个数的乘积。**若 i 从 0 出发,则记为: n ! i + 1 \frac{n!}{i+1} i+1n!
每一列的价值总数又可以记为: i ∗ ( i + 1 ) 2 \frac{i*(i+1)}{2} 2i∗(i+1)
综上所述:
n 的 全 排 列 价 值 = ∑ i = 0 i = n − 1 i ∗ ( i + 1 ) 2 ∗ n ! i + 1 n的全排列价值 = \sum_{i=0}^{i=n-1} \frac{i*(i+1)}{2}* \frac{n!}{i+1} n的全排列价值=i=0∑i=n−12i∗(i+1)∗i+1n!
化简:
n 的 全 排 列 价 值 = n ! 2 ∗ ∑ i = 0 i = n − 1 i n的全排列价值 =\frac{n!}{2}* \sum_{i=0}^{i=n-1} i n的全排列价值=2n!∗i=0∑i=n−1i
import math
from collections import Counter
n = int(input())
ans = sum(range(n))*math.factorial(n)//2%998244353
print(ans)
参考链接
H、技能升级
✨试题链接
直接暴力解法,其实直接按攻击力 A i A_i Ai循环从大到小排序即可。
向上取整的条件 ⌈ A i B i ⌉ \lceil \frac{A_i}{B_i} \rceil ⌈BiAi⌉其实就是保证 A i − B i A_i-B_i Ai−Bi为正数,不会使攻击力减小。只需要判断一下a[0][0]正负就行。

n,m = map(int,input().split())
a = []
for i in range(n):
a.append(list(map(int,input().split())))
ans = 0
while m>0:
a = sorted(a,key=lambda x:x[0],reverse=True)
if a[0][0]>0:
ans += a[0][0]
a[0][0] -= a[0][1]
m -= 1
else:
break
print(ans)
I、最长不下降子序列
我的想法是,根据动态规划,可以先写出求最长不下降子序列的函数。然后遍历依次改变列表中k个值,变为最大或最小,在判断其最长序列长度。输出最长序列。
但细想一下,方法应该不对,而且复杂度很高!
希望有大佬解答,这两个 大佬链接1 大佬链接2也可以做参考!
import copy
n,k = map(int,input().split())
arg = list(map(int,input().split()))
def lis(*args,num=1):
d = [0]*num
len_num = 1
for i in range(num):
d[i] = 1
for j in range(i):
if args[j]<=args[i] and d[i]<d[j]+1:
d[i]=d[j]+1
if d[i]>len_num:
len_num = d[i]
return len_num
nums = []
for i in range(n-k+1):
b = copy.deepcopy(arg)
c = copy.deepcopy(arg)
b[i:i+k] = map(lambda x:x-x+1,b[i:i+k])
c[i:i+k] = map(lambda x:x*pow(10,6),c[i:i+k])
nums.append(lis(*b,num=n))
nums.append(lis(*c,num=n))
print(max(nums))
J、最优清零方案
n,k = map(int,input().split())
a = list(map(int,input().split()))
num = 0
s = 0
while s < n-k+1:
b = a[s:s+k]
if 0 in b:
s = a[s:s+k].index(0)+s+1 #0在a[s:s+k]中的索引
else:
a[s:s+k] = map(lambda x:x-1,a[s:s+k])
num += 1
nums = num+sum(a)
print(nums)







