第十三届蓝桥杯省赛 python B组复盘

---

前言

备战蓝桥杯第一弹–复盘

---

主要内容

试题 A：排列字母

思路

(当时第一次参加蓝桥杯，当时现场心里小鹿乱撞，用排序输出了还每个字母数数验证一番(滑稽))

• 字符串转列表
• 列表排序
• 列表转字符串

代码

l = "WHERETHEREISAWILLTHEREISAWAY"
print(''.join(sorted(l))) 
# AAAEEEEEEHHHIIILLRRRSSTTWWWY

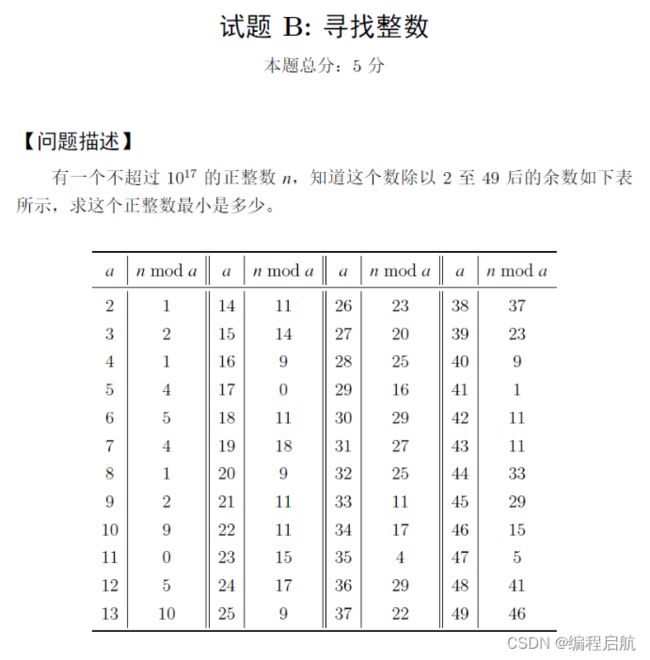
试题 B：寻找整数

思路

当时在现场程序没跑出来
想着那个数取余2余1，取余4余1，取余8余1可以只看取余8余1的，因为满足后者一定满足前者，而满足前者不一定满足后者，不过当时没有想到找等差数列，一直在等最后的结果。。。

之后看大神的是有三个步骤：
暴力三步走：
1.枚举数据找规律：取表后面5个大数判断更容易找到大数据，得到关键数据。
2.找出规律求公式：这些数字是按判断求得的，所以一定存在公式。
3.遍历公式找答案：通过公式进行快速遍历，30s轻松找到十六位数的答案。

代码

#1.枚举数据找规律
i=1
while True:
    flag=True
    if i%49!=46:
        flag=False
    if i%48!=41:
        flag=False
    if i%47!=5:
        flag=False
    if i%46!=15:
        flag=False
    if i%45!=29:
        flag=False
    if flag:
        print(i)
    i+=1
'''
4772009
42909689
81047369
119185049
157322729
···
'''

#2.找出规律求公式
a=[4772009, 42909689, 81047369, 119185049,157322729]
#发现存在等差数列
print(a[1]-a[0])#38137680
print(a[2]-a[1])#38137680
print(a[3]-a[2])#38137680
k=38137680
b=4772009
#求出公式
y=k

#遍历公式
x=0
k=38137680
b=4772009
while True:
    flag=True
    y=k*x+b
    for i,j in mod:
        if y%i !=j:
            flag=False
            break
    if flag==True:
        print(y)#2022040920220409
        break
    x+=1

试题 C：纸张尺寸

题目描述
在 ISO 国际标准中定义了 A0 纸张的大小为 1189mm × 841mm，将 A0 纸沿长边对折后为 A1 纸，大小为 841mm × 594mm，在对折的过程中长度直接取下整（实际裁剪时可能有损耗）。将 A1 纸沿长边对折后为 A2 纸，依此类推。
输入纸张的名称，请输出纸张的大小。
输入
输入一行包含一个字符串表示纸张的名称，该名称一定是 A0、A1、A2、A3、A4、A5、A6、A7、A8、A9 之一。
输出
输出两行，每行包含一个整数，依次表示长边和短边的长度。
样例输入
A0
1
样例输出
1189
841

思路

当时就想着简单的判断循环
操作是折叠纸张
A几就是折叠几次，对应循环操作了几次

• 获取输入
• 循环次数
• 循环的操作
• 输出

代码

s = input() 

t = int(s[-1]) # 最后一个数字也就是迭代的次数
w,h = 1189,841

for i in range(t):
    if w > h:
        w = w//2
    else:
        h = h//2
if w > h:
    print(w)
    print(h)
else:
    print(h)
    print(w)

试题 D：数位排序

小蓝对一个数的数位之和很感兴趣，今天他要按照数位之和给数排序。当两个数各个数位之和不同时，将数位和较小的排在前面，当数位之和相等时，将数值小的排在前面。
例如，2022 排在 409 前面，因为 2022 的数位之和是 6，小于 409 的数位之和 13。
又如，6 排在 2022 前面，因为它们的数位之和相同，而 6 小于 2022。
给定正整数 n，m，请问对 1 到 n 采用这种方法排序时，排在第 m 个的元素是多少？
输入
输入第一行包含一个正整数 n。
第二行包含一个正整数 m。
输出
输出一行包含一个整数，表示答案。
样例输入
13
5
样例输出
3
提示
1 到 13 的排序为：1, 10, 2, 11, 3, 12, 4, 13, 5, 6, 7, 8, 9。第 5 个数为 3。
对于 30% 的评测用例，1 ≤ m ≤ n ≤ 300
对于 50% 的评测用例，1 ≤ m ≤ n ≤ 1000
对于所有评测用例，1 ≤ m ≤ n ≤ 10⁶

思路

当时现场用的方法很绕写出来的，后来发现只是重新定义了一下排序规则

• 计算数位之和
• 定义排序规则

代码

n = int(input())
m = int(input())
l = [i for i in range(1,n+1)]
# 设置一个排序规则，计算数位之和
def fun(x):
    ans = 0
    while x:
        ans += x%10
        x = x//10
    return ans 

l.sort(key = fun)
print(l[m-1])

试题 E：蜂巢

题目描述
蜂巢由大量的六边形拼接而成，定义蜂巢中的方向为：0 表示正西方向，1 表示西偏北 60◦，2 表示东偏北 60◦，3 表示正东，4 表示东偏南 60◦，5 表示西偏南 60◦。
对于给定的一点 O，我们以 O 为原点定义坐标系，如果一个点 A 由 O 点先向 d 方向走 p 步再向 (d + 2) mod 6 方向（d 的顺时针 120◦ 方向）走 q 步到达，则这个点的坐标定义为 (d, p, q)。在蜂窝中，一个点的坐标可能有多种。
下图给出了点 B(0, 5, 3) 和点 C(2, 3, 2) 的示意。

给定点 (d1, p1, q1) 和点 (d2, p2, q2)，请问他们之间最少走多少步可以到达？
输入
输入一行包含 6 个整数 d1, p1, q1, d2, p2, q2 表示两个点的坐标，相邻两个整数之间使用一个空格分隔。
输出
输出一行包含一个整数表示两点之间最少走多少步可以到达。
样例输入
0 5 3 2 3 2
样例输出
7
提示
对于 25% 的评测用例，p1, p2 ≤ 10³
对于 50% 的评测用例，p1, p2 ≤10⁵
对于 75% 的评测用例，p1, p2 ≤10⁷
对于所有评测用例，0 ≤ d1, d2 ≤ 5，0 ≤ q1 < p1 ≤ 10⁹ ，0 ≤ q2 < p2 ≤ 10⁹

思路

比赛的时候没有做出来，当时也是入门算法，读完题毫无思路，感慨万千

现在看了网上的回答用向量来做，将坐标的表达方式转化为向量，统一为0和1方向的向量。一共有六个方向，也就是六种计算方式。

代码

d1,p1,q1,d2,p2,q2=map(int,input().split())

# 全部转化为0 方向 和 1方向的向量
def change(d,p,q):
    if d==0:return (p-q,q)
    if d==1:return (-q,p)
    if d==2:return (-p,p-q)
    if d==3:return (q-p,-q)
    if d==4:return (q,-p)
    if d==5:return (p,q-p)
s1=change(d1,p1,q1)
s2=change(d2,p2,q2)

# 向量的减法
s=[s1[0]-s2[0],s1[1]-s2[1]]
a,b=s[0],s[1]
if a*b > 0: 
    # ab同号
    print(abs(a+b))
else: 
    # ab异号
  	print(max(abs(a),abs(b)))

试题 F：消除游戏

题目描述

输入
输入一行包含一个字符串 S 。
输出
输出一行包含一个字符串表示答案，如果结果为空则输出 EMPTY。
样例输入
edda
样例输出
EMPTY
样例输入
sdfhhhhcvhhxcxnnnnshh
样例输出
s
提示
对于 25% 的评测用例，|S | ≤ 10³ ，其中 |S | 表示 S 的长度；
对于 50% 的评测用例，|S | ≤ 10⁴
对于 75% 的评测用例，|S | ≤ 10⁵
对于所有评测用例，|S | ≤ 10⁶ ，S 中仅含小写字母。

思路

当时读完题感觉2⁶⁴非常大，直接写了一个无限循环，一直循环听说只可以过75%的数据

代码

s = input()
def f(x):
    s = set()
    for i in range(1,len(x)-1):
        if (x[i] == x[i-1] and x[i] != x[i+1]):
            s.add(i)
            s.add(i+1)
        elif (x[i] != x[i-1] and x[i] == x[i+1]):
            s.add(i-1)
            s.add(i) 
    sr = ''
    for i in range(len(x)):
        if i not in s:
            sr += x[i]
    return sr
import copy
# 2的64次方操作
for i in range(1<<64):
    pre = copy.copy(s)
    s = f(s)
    if s == '':
        print('EMPTY')
        break
    elif pre == s:
        print(s)
        break

试题 G：全排列的价值

输入
输入一行包含一个整数 n 。
输出
输出一行包含一个整数表示答案，由于所有排列的价值之和可能很大，请输出这个数除以 998244353 的余数。
样例输入
3
样例输出
9
提示
1 至 3 构成的所有排列的价值如下:
(1, 2, 3) : 0 + 1 + 2 = 3
(1, 3, 2) : 0 + 1 + 1 = 2
(2, 1, 3) : 0 + 0 + 2 = 2
(2, 3, 1) : 0 + 1 + 0 = 1
(3, 1, 2) : 0 + 0 + 1 = 1
(3, 2, 1) : 0 + 0 + 0 = 0
故总和为 3 + 2 + 2 + 1 + 1 = 9
对于 40% 的评测用例，n ≤ 20
对于 70% 的评测用例，n ≤ 5000
对于所有评测用例，2 ≤ n ≤ 10⁶

思路

当时在在考场上猜到是动态规划，一直在找规律，也不知道找对没
看大佬们的解法，太感人了，太优雅了

代码

MOD = 998244353
n = int(input().strip())
dp = 0
f = 1
for i in range(2,n+1):
    dp = (dp*i+f*i*(i-1)//2)%MOD
    f = f*i%MOD
print(dp)

试题 H：技能升级

样例输入
3 6
10 5
9 2
8 1
样例输出
47
提示
对于 40% 的评测用例，1 ≤ N, M ≤ 1000；
对于 60% 的评测用例，1 ≤ N ≤ 104 , 1 ≤ M ≤ 107；
对于所有评测用例，1 ≤ N ≤ 105，1 ≤ M ≤ 2 × 109，1 ≤ Ai , Bi ≤ 106。

思路

考场上用的是暴力，这里我们来看看大佬的思路

首先来说，我先自己做了一下，然后想到一个根据优先队列的做法，我只需要每次取得最优的，那我从某种意义来说，我们最后的结果就是最优的。

所以构建一个最大堆，然后每次取到最大的数，然后再push一个数进去，就是我们会更新我们的数，不过我们这个堆，一直都只有n个数据，我们把最大的pop出来以后，我们就可以进行更新，比如说减去b，或者变成0后不再进行技能升级。

所以依靠这样的想法，我就写了一下，而且我们在想，这样子，我们的读入数据是O（n），处理数据加上一个堆的排序，可能是nlogn，这样子应该是可以的。

这里提一下，我觉得最小堆和最大堆他是可以互换的，由于我好想发现heapq的最大堆没有push操作，那我就把数变成负的，这样我就利用最小堆构建了一个最大堆，因为加了一个负号后，最大的就变成最小的了

代码

import heapq

n,m = map(int,input().split())
a,b = [],[]

heap = []
for i in range(n):
    x,y = map(int,input().split())
    a.append(x)
    b.append(y)
    heapq.heappush(heap,(-x,i,0))

cnt = 0
import math
for i in range(m):
    x,y,z = heapq.heappop(heap)
    if x == 0:
        break
    x=-x
    cnt += x
    # x,y = nlargest(1,heap)
    if z > math.ceil(a[y]/b[y]):  
        x = 0
        continue
    else:
        x = x - b[y]
    heapq.heappush(heap,(-x,y,z+1))
    
print(cnt)

试题 I：最长不下降子序列

样例输入
5 1
1 4 2 8 5
样例输出
4
提示
对于 20% 的评测用例，1 ≤ K ≤ N ≤ 100；
对于 30% 的评测用例，1 ≤ K ≤ N ≤ 1000；
对于 50% 的评测用例，1 ≤ K ≤ N ≤ 10000；
对于所有评测用例，1 ≤ K ≤ N ≤ 10⁵，1 ≤ Ai ≤ 10⁶

思路

看看大佬怎末说

代码

试题 J：最优清零方案

题目描述
给定一个长度为 N 的数列 A1, A2, · · · , AN。现在小蓝想通过若干次操作将这个数列中每个数字清零。
每次操作小蓝可以选择以下两种之一：
选择一个大于 0 的整数，将它减去 1；
选择连续 K 个大于 0 的整数，将它们各减去 1。
小蓝最少经过几次操作可以将整个数列清零？
输入
输入第一行包含两个整数 N 和 K。
第二行包含 N 个整数 A1, A2, · · · , AN。
输出
输出一个整数表示答案。
样例输入复制
4 2
1 2 3 4
样例输出复制
6
提示
对于 20% 的评测用例，1 ≤ K ≤ N ≤ 10。
对于 40% 的评测用例，1 ≤ K ≤ N ≤ 100。
对于 50% 的评测用例，1 ≤ K ≤ N ≤ 1000。
对于 60% 的评测用例，1 ≤ K ≤ N ≤ 10000。
对于 70% 的评测用例，1 ≤ K ≤ N ≤ 100000。
对于所有评测用例，1 ≤ K ≤ N ≤ 1000000, 0 ≤ Ai ≤ 1000000。

思路

代码

总结

☝️ ⭐

如果你对这篇文章感兴趣，欢迎在评论区留言，分享你的想法和建议。如果你喜欢我的博客，请记得点赞、收藏和关注我，我会持续更新更多有用的网页技巧和教程。谢谢大家！

---

更多宝藏

项目仓库看这里：
https://github.com/w-x-x-w
https://gitee.com/w-_-x
博客文章看这里：
https://blog.csdn.net/weixin_62650212
视频推送看这里：
https://space.bilibili.com/1909782963