一、基础算法5：前缀和与差分 模板题+算法模板（前缀和，子矩阵的和，差分，差分矩阵）

算法模板

前缀和模板

S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

子矩阵的和模板

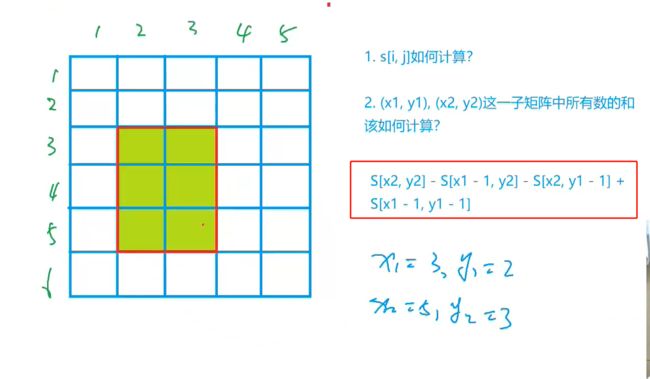
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

差分模板

给区间[l, r]中的每个数加上c：B[l] += c, B[r + 1] -= c

差分矩阵模板

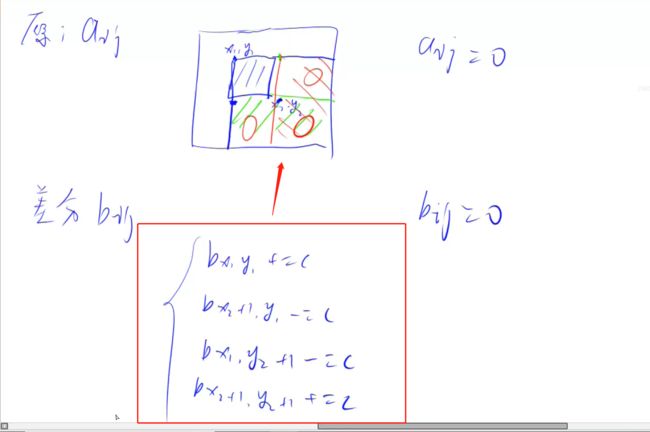
给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, 
S[x2 + 1, y1] -= c, 
S[x1, y2 + 1] -= c, 
S[x2 + 1, y2 + 1] += c

模板题

前缀和

原题链接

https://www.acwing.com/problem/content/797/

题目

795 . 前缀和
输入一个长度为 n 的整数序列。

接下来再输入 m 个询问，每个询问输入一对 l,r。

对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。

输入格式
第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

接下来 m 行，每行包含两个整数 l 和 r，表示一个询问的区间范围。

输出格式
共 m 行，每行输出一个询问的结果。

数据范围
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000
输入样例：

5 3
2 1 3 6 4
1 2
1 3
2 4

输出样例：

3
6
10

题解

#include 
using namespace std;

const int N = 1e5 +10;

int a[N],s[N];

int n,m;
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	
	for(int i=1;i<=n;i++) s[i] = s[i-1] + a[i];
	
	while(m--){
		int l,r;
		scanf("%d%d",&l,&r);
		printf("%d\n",s[r] - s[l-1]);
		
	}
	return 0;
}

子矩阵的和

原题链接

https://www.acwing.com/problem/content/798/

题目

796 . 子矩阵的和
输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式
第一行包含三个整数 n，m，q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。

输出格式
共 q 行，每行输出一个询问的结果。

数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000
输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：

17
27
21

题解

#include 
using namespace std;
const int N = 1010;
int n,m,q;

int a[N][N],s[N][N];
int main(){
	scanf("%d%d%d",&n,&m,&q);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			scanf("%d",&a[i][j]);
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] +a[i][j];
		}
	}
	while(q--){
		int x1,y1,x2,y2;
		scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		printf("%d\n",s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]);
	}
	return 0;
}

差分

原题链接

https://www.acwing.com/problem/content/799/

题目

797 . 差分

输入一个长度为 n 的整数序列。

接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。

输出格式
共一行，包含 n 个整数，表示最终序列。

数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例：

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例：

3 4 5 3 4 2

题解

#include 
using namespace std;
const int N = 1e5 + 10;

int n,m;
int a[N],b[N];

void insert(int l,int r,int c){
	b[l]+=c;
	b[r+1]-=c;
}
int main(){
	scanf("%d%d",&n,&m);
	
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	
	for(int i=1;i<=n;i++) insert(i,i,a[i]);
	
	while(m--){
		int l,r,c;
		scanf("%d%d%d",&l,&r,&c);
		insert(l,r,c);
		
	}
	for(int i=1;i<=n;i++) b[i]+=b[i-1]; //差分数组-->前缀和数组
	
	for(int i=1;i<=n;i++) printf("%d ",b[i]);
	
	return 0; 
}

差分矩阵

原题链接

https://www.acwing.com/problem/content/800/

题目

798 . 差分矩阵
输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数 n,m,q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。

输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例：

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

输出样例：

2 3 4 1
4 3 4 1
2 2 2 2

题解

#include 
using namespace std;
const int N = 1010;

int n,m,q;
int a[N][N],b[N][N];

void insert(int x1,int y1,int x2,int y2,int c){
	b[x1][y1]+=c;
	b[x1][y2+1]-=c;
	b[x2+1][y1]-=c;
	b[x2+1][y2+1]+=c;
}
int main(){
	cin>>n>>m>>q;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			scanf("%d",&a[i][j]);
		}
	}
	
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			insert(i,j,i,j,a[i][j]);
		}
	}
	
	while(q--){
		int x1,y1,x2,y2,c;
		cin>>x1>>y1>>x2>>y2>>c;
		insert(x1,y1,x2,y2,c);
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			b[i][j] += b[i-1][j] + b[i][j-1] - b[i-1][j-1];
		} 
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			printf("%d ",b[i][j]);
			
		}
		puts(""); //相当于输出换行符 
	}
	return 0;
	
}