算法学习day50

1.力扣123.买卖股票的最佳时机III

1.1 分析

题目描述：

给定一个数组，它的第i个元素是一支给定的股票在第i天的价格。

设计一个算法来计算你所能获得的最大利润。最多可以完成两笔交易。

例1：

输入：prices=[3 , 3, 5, 0, 0, 3, 1, 4]

输出：6

解释：在第4天（股票价格为0）的时候买入，在第6天（股票价格为3）的时候卖出，得到利润3.

随后在第7天（股票价格为1）的时候买入，在第8天（股票价格为4）的时候卖出，交易所能获得的利润为4-1 = 3.

动规五部曲

1.确定dp数组以及下标的含义

一天一共5个状态：

0表示没有操作

1表示第一次持有股票

2表示第一次不持有股票

3表示第二次持有股票

4表示第二次不持有股票

dp[i] [j]中i表示第i天，j为[0 - 4]五个状态，dp[i] [j] 表示第i天状态j所剩最大现金。

2.确定递推公式

达到dp[i] [1] 状态，有两个具体操作：

(1) 第i天买入股票了，那么dp[i] [1] = dp[i-1] [0] - prices[i]

(2) 第i天没有操作，而是沿用前一天买入的状态,dp[i] [1] = dp[i-1] [1].

递推公式:dp[i] [1] = max(dp[i-1] [0] - prices[i], dp[i-1] [1])

达到dp[i] [2] 状态，有两个具体操作：

(1) 第i天卖出股票了，那么dp[i] [2] = dp[i-1] [1] + prices[i]

(2) 第i天没有操作，而是沿用前一天买入的状态,dp[i] [2] = dp[i-1] [2].

递推公式:dp[i] [2] = max(dp[i-1] [1]+prices[i], dp[i-1] [2])

同理得：

递推公式:dp[i] [3] = max(dp[i-1] [3], dp[i-1] [2] - prices[i])

递推公式:dp[i] [4] = max(dp[i-1] [4], dp[i-1] [3] + prices[i])

3.dp数组如何初始化

第0天没有操作：dp[0] [0] = 0;

第0天做一次买入操作:dp[0] [1] = -prices[0];

第0天做一次卖出操作：dp[0] [2] = 0;

第0天第二次买入操作：dp[0] [ 3] = -price[0];

第0天第二次卖出操作:dp[0] [4] = 0;

4.确定遍历顺序

从前向后遍历，因为dp[i]依靠dp[i-1]的数量

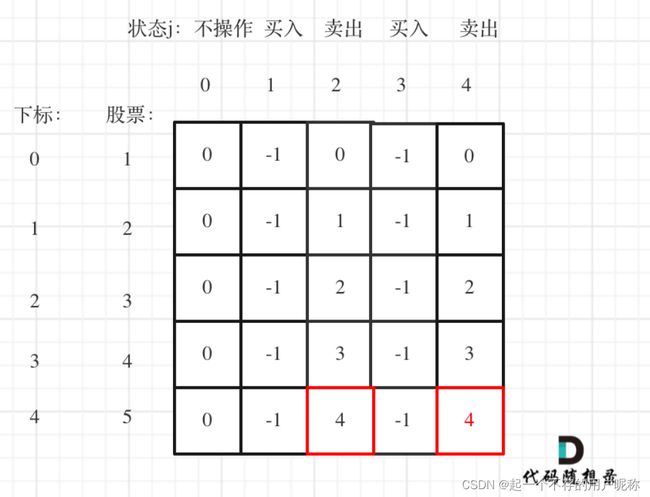
5.举例推导dp数组

1.2 代码

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.size() == 0) return 0;                                                       // 如果prices为空，则返回0。
        vector<vector<int>> dp(prices.size(), vector<int>(5, 0)); // 初始化dp数组，大小为 prices.size() x 5。
        dp[0][1] = -prices[0];                                                                       // 初始化第一天买入的状态，即dp[0][1]为 -prices[0]。
        dp[0][3] = -prices[0];                                                                       // 初始化第二次买入的状态，即dp[0][3]为 -prices[0]。
        for (int i = 1; i < prices.size(); i++) {                                            // 从第二天开始遍历prices数组。
            dp[i][0] = dp[i - 1][0];                                                                  // 第i天不做任何操作，状态不变，即dp[i][0] = dp[i-1][0]。
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]); // 第i天进行一次买入操作，即dp[i][1]的值为前一天已经持有股票或者前一天没有进行操作而今天进行买入操作两种情况中的最大值。
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]); // 第i天进行一次卖出操作，即dp[i][2]的值为前一天已经卖出股票或者前一天持有股票而今天进行卖出操作两种情况中的最大值。
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]); // 第i天进行第二次买入操作，即dp[i][3]的值为前一天已经持有股票或者前一天没有进行操作而今天进行买入操作两种情况中的最大值。
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]); // 第i天进行第二次卖出操作，即dp[i][4]的值为前一天已经卖出股票或者前一天持有股票而今天进行卖出操作两种情况中的最大值。
        }
        return dp[prices.size() - 1][4]; // 返回最终状态下的最大收益，即dp[prices.size() - 1][4]。
    }
};

2.力扣188.买卖股票的最佳时机IV

2.1 分析

题目描述：

给定一个整数数组prices,它的第i个元素prices[i]是一支给定的股票在第i天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

例 1：

输入：k = 2, prices = [2,4,1]

输出：2

解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2。

例 2：

输入：k = 2, prices = [3,2,6,5,0,3]

输出：7

解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4。随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

1.确定dp数组以及下标的含义

dp[i] [j]:第i天的状态为j，所剩下的最大现金是dp[i] [j]

j的状态表示为：

• 0 表示不操作
• 1 第一次买入
• 2 第一次卖出
• 3 第二次买入
• 4 第二次卖出

归纳：除了0以外，偶数就是卖出，奇数就是买入。

题目要求k笔交易可知j的范围为2 * k + 1即可

vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));

2.确定递推公式

达到dp[i] [1]状态，有以下两个操作：

(1)第i天买入股票了，那么dp[i] [1] = dp[i - 1] [0] - prices[i]

(2)第i天没有操作，而是沿用前一天买入的状态，即：dp[i] [1] = dp[i - 1] [1]

递推公式**：dp[i] [1] = max(dp[i-1] [0] - prices[i], dp[i-1] [1]);**

达到dp[i] [2] 状态，有以下两个操作：

(1) 第i天卖出股票了，那么dp[i] [2] = dp[i - 1] [1] + prices[i]

(2) 第i天没有操作，沿用前一天卖出股票的状态，dp[i] [2] = dp[i - 1] [2]

递推公式:dp[i] [2] = max(dp[i-1] [1] + prices[i] , dp[i - 1] [2]);

3.dp数组如何初始化

第0天没有操作：dp[0] [0] = 0;

第0天做一次买入操作:dp[0] [1] = -prices[0];

第0天做一次卖出操作：dp[0] [2] = 0;

第0天第二次买入操作：dp[0] [ 3] = -price[0];

第0天第二次卖出操作:dp[0] [4] = 0;

4.确定遍历顺序

从前向后

5.举例推导dp数组

2.2 代码

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        // 判断特殊情况，如果股票价格数组为空，则无法交易，返回0
        if (prices.size() == 0) return 0;
        
        // 定义一个二维数组dp，dp[i][j]表示第i天时，状态为j的最大利润
        // 状态0表示没有持有股票且没有进行任何交易，状态1表示持有股票且没有进行任何交易，
        // 状态2表示没有持有股票且进行了1次交易，状态3表示持有股票且进行了1次交易，
        // 状态4表示没有持有股票且进行了2次交易，以此类推
        vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
        
        // 初始化dp数组，第0天的状态
        for (int j = 1; j < 2 * k; j += 2) {
            dp[0][j] = -prices[0]; // 在状态1中，持有股票的成本为第0天的股票价格
        }
        
        // 遍历所有天数，计算每天的状态
        for (int i = 1; i < prices.size(); i++) {
            // 遍历所有状态，计算当前天数下的最大利润
            for (int j = 0; j < 2 * k - 1; j += 2) {
                // 计算状态j+1下的最大利润，即在当前天数购买股票后的最大利润
                dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
                // 计算状态j+2下的最大利润，即在当前天数卖出股票后的最大利润
                dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
            }
        }
        
        // 返回最后一天状态为2k的最大利润，即进行了2k次交易后的最大利润
        return dp[prices.size() - 1][2 * k];
    }
};

3.参考资料

[代码随想录]