算法学习day52
算法学习day52
- 1.力扣 300.最长递增子序列
-
- 1.1 题目描述
- 1.2分析
- 1.3 代码
- 2.力扣674. 最长连续递增序列
-
- 2.1 题目描述
- 2.2 分析
- 2.3 代码
- 3.力扣718. 最长重复子数组
-
- 3.1 题目描述
- 3.2 分析
- 3.3 代码
- 3.参考资料
1.力扣 300.最长递增子序列
1.1 题目描述
题目描述:
给一个整数数组nums , 找到其中最长严格递增子序列的长度。
子序列是数组派生而来,可以删除(不删除数组中的元素而不改变其余元素的顺序),例如:[3 , 6 , 2 ,7]是数组[0 , 3, 1, 6 ,2 ,2 ,7]的子序列
例 1:
- 输入:nums = [10,9,2,5,3,7,101,18]
- 输出:4
- 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
例 2:
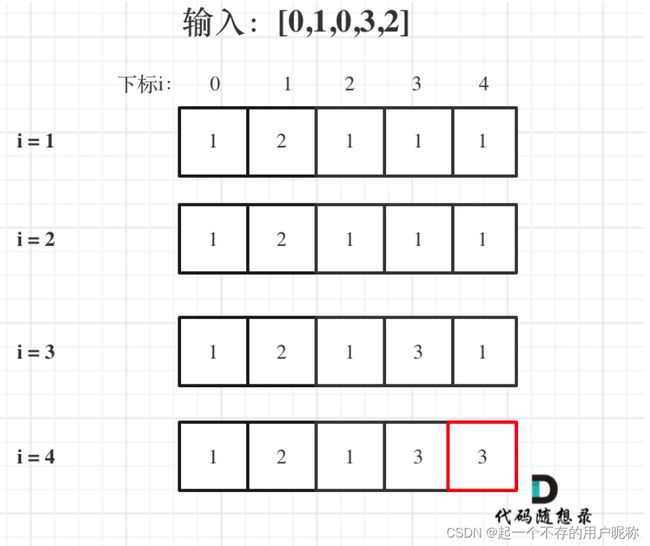
- 输入:nums = [0,1,0,3,2,3]
- 输出:4
例 3:
- 输入:nums = [7,7,7,7,7,7,7]
- 输出:1
1.2分析
动规五部曲
1.dp[i]的定义
dp[i]:表示i之前包括i的以nums[i]结尾的最长递增子序列的长度。
2.递推公式
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列+1的最大值。
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
3.dp[i]的初始化
每一个i,对应的dp[i](最长递归子序列)起始大小至少都是1.
4.确定遍历顺序
dp[i]是有0到i-1个位置的最长递归子序列推导的,遍历是从前往后遍历。
for(int i = 1 ; i < nums.size() ; i++){
for(int j = 0 ; j < i ; j++){
// dp[i]表示以nums[i]为结尾的最长上升子序列长度
// 对于任意的1<=j
// 更新dp[i] 的值为dp[j] + 1
if(nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] +1);
}
if(dp[i] > result) result = dp[i]; // 取长的子序列
}
5.举例推导dp数组
1.3 代码
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
if (nums.size() <= 1) return nums.size(); // 特判
vector<int> dp(nums.size(), 1); // dp[i] 表示以 nums[i] 结尾的 LIS 的长度
int result = 0; // 存储最长的 LIS 长度
for (int i = 1; i < nums.size(); i++) { // 枚举结尾位置
for (int j = 0; j < i; j++) { // 枚举 LIS 中倒数第二个位置
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1); // 如果 nums[i] 比前面的某个数 nums[j] 大,则可以将 nums[i] 接到以 nums[j] 结尾的 LIS 后面
}
if (dp[i] > result) result = dp[i]; // 取长的子序列
}
return result; // 返回最长的 LIS 长度
}
};
2.力扣674. 最长连续递增序列
2.1 题目描述
题目描述:
给定一个未经排序的整数数组,找到最长且连续递增的子序列,并返回该序列的长度。
连续递增的子序列可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。
例 1:
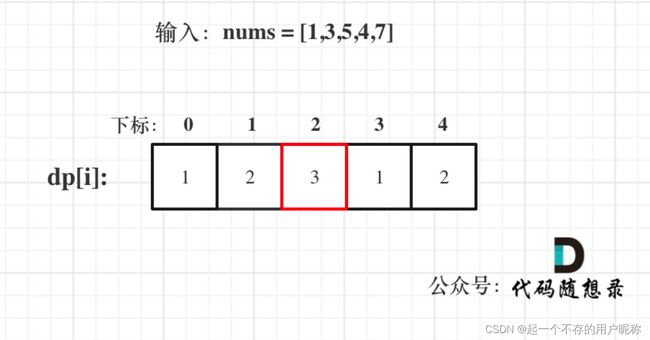
- 输入:nums = [1,3,5,4,7]
- 输出:3
- 解释:最长连续递增序列是 [1,3,5], 长度为3。尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
例 2:
- 输入:nums = [2,2,2,2,2]
- 输出:1
- 解释:最长连续递增序列是 [2], 长度为1。
2.2 分析
动规五部曲
1.确定dp数组以及下标的含义
dp[i]:以下标i为结尾的连续递增子序列长度为dp[i]。
2.确定递推公式
如果nums[i] > nums[i - 1],那么以i结尾的连续递增子序列长度一定等于以i-1为结尾的连续递增子序列长度+1。
dp[i] =dp[i - 1] + 1
3.dp数组如何初始化
dp[i]初始化为1
4.确定遍历顺序
for(int i = 1 ; i < nums.size() ; i++){
if(nums[i] > nums[i - 1]){ // 连续记录
dp[i] = dp[i-1]+1;
}
}
2.3 代码
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
if (nums.size() == 0) return 0; // 数组为空时返回0
int result = 1; // 初始化结果为1,因为至少有一个元素是递增子序列
vector<int> dp(nums.size() ,1); // 定义dp数组,dp[i]表示以第i个元素结尾的最长连续递增子序列的长度
for (int i = 1; i < nums.size(); i++) { // 遍历数组,从第2个元素开始,因为第1个元素默认是递增子序列的开头
if (nums[i] > nums[i - 1]) { // 如果当前元素比前一个元素大,说明是连续递增的一部分
dp[i] = dp[i - 1] + 1; // 当前元素的最长递增子序列长度为前一个元素的最长递增子序列长度+1
}
if (dp[i] > result) result = dp[i]; // 更新结果
}
return result; // 返回结果
}
};
3.力扣718. 最长重复子数组
3.1 题目描述
题目描述:
给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
例:
输入:
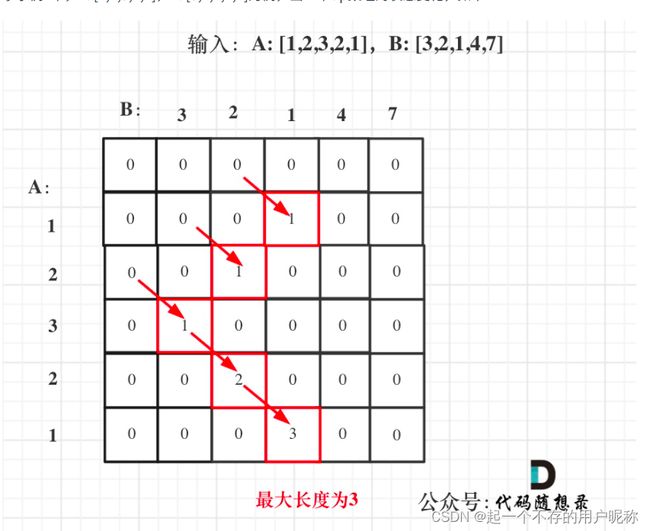
- A: [1,2,3,2,1]
- B: [3,2,1,4,7]
- 输出:3
- 解释:长度最长的公共子数组是 [3, 2, 1] 。
3.2 分析
1.确定dp数组以及下标的含义
dp[i] [j] :以下标i - 1结尾的A,和以下标j - 1结尾的B,最长重复子数组长度为dp[i] [j].
2.确定递推公式
dp[i] [j] = dp[i-1] [j-1]
3.dp数组如何初始化
dp[i] [0] = 0;
dp[0] [j] = 0;
4.确定遍历顺序
for (int i = 1; i <= nums1.size(); i++) {
for (int j = 1; j <= nums2.size(); j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
if (dp[i][j] > result) result = dp[i][j];
}
}
5.举例推导dp数组
3.3 代码
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
// 初始化一个二维数组dp,其中dp[i][j]表示nums1[0:i-1]与nums2[0:j-1]的最长公共子数组长度
vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
// 初始化结果变量result
int result = 0;
// 两重循环,枚举所有可能的子数组
for (int i = 1; i <= nums1.size(); i++) {
for (int j = 1; j <= nums2.size(); j++) {
// 如果nums1和nums2在当前位置的数相等,则当前位置的dp值为左上角位置的dp值加1
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
// 更新结果变量
if (dp[i][j] > result) result = dp[i][j];
}
}
// 返回结果变量
return result;
}
};
3.参考资料
[代码随想录]