数据结构与算法整理7——树与二叉树(C语言)
数据结构与算法整理7——树与二叉树(C语言)
目录
数据结构与算法整理7——树与二叉树(C语言)
1、树和二叉树的概念
1.1 树
1.2 二叉树
1.3 二叉树的分类
1.4 二叉树的性质
1.5 二叉树的存储方式
1.6 线索二叉树
2、二叉树的周游,中,先—>后,画树
3、哈夫曼算法及哈夫曼编码,WPL的计算
3.1 哈夫曼树相关概念
3.2 哈夫曼树的构造
3.3 哈夫曼树编码
4、二叉树与树的转换
4.1树的表示方法
4.2树与二叉树的转换
5、二叉树与哈夫曼树操作代码(C语言)
(1)二叉树的顺序存储与周游
(2)二叉树的链式存储与周游
(3)哈夫曼树的操作
1、树和二叉树的概念
1.1 树
树:即树形结构,是数据逻辑结构的一种。
(1)特点:每个结点最多一个前驱结点,多个后继结点
(2)度的概念:结点的度就是结点的孩子数,树的度就是所有结点的度的最大值。
(3)深度的概念:根的层次为0,依次往下数。
(4)实例:磁盘文件的目录结构。
(5)有序树与无序树:即对子树是否加以区别。
1.2 二叉树
二叉树:结点有限,区分左右子树的有序树。二叉树不是树的特殊情况,树与二叉树的区别在于二叉树是有序的。
1.3 二叉树的分类
1.4 二叉树的性质
1.5 二叉树的存储方式
(1)顺序存储:采用一组连续的存储单元存放二叉树的节点,没有节点的地方需要^补上。
(2)链式存储:用一条链表储存二叉树,一个节点有数据域和两个左右孩子的指 针组成,若没有左/右孩子用^表示
| lchild |
data |
rchild |
1.6 线索二叉树
1、定义:增加节点标志域,利用这些指针把节点的前驱和后继的节点的信息连接起来,建立线索二叉树,主要是为了保留在各种遍历时得到的节点前驱和后继节点信息(即保留在各种遍历时产生的线性关系)。
| Lefttag |
lchild |
data |
rchild |
righttag |
2、实例:中序周游的结果是:CDBAEGHTF,有边相连就无需用虚线相连,无边相连则用虚线连起来。
2、二叉树的周游,中,先—>后,画树
|
|
先序周游 |
中序周游 |
后序周游 |
| 顺序 |
根左右 |
左根右 |
左右根 |
| 实例 |
*+ab-cd |
A+b*c-d |
Ab+cd-* |
| 递归运算 |
void postOrder(BNode p) { if (p == NULL) return; visit(p); postOrder(leftChild_btree(p)); postOrder(rightChild_btree(p));} |
void postOrder(BNode p) { if (p == NULL) return; postOrder(leftChild_btree(p)); visit(p); postOrder(rightChild_btree(p));} |
void postOrder(BNode p) {if (p == NULL) return; postOrder(leftChild_btree(p)); postOrder(rightChild_btree(p)); visit(p);} |
3、哈夫曼算法及哈夫曼编码,WPL的计算
3.1 哈夫曼树相关概念
(1)路径长度:从A->B所经过的分支序列称路径,经过的分支个数称为路径长度。
(2)带权路径长度:若二叉树中的叶节点都带有权值,从根节点到叶节点的路径长度与相应的叶节点权值乘积之和称为该树的带 权路径长度(WPL)。 WPL=wi*pi在[1,n]求和。
(3)哈夫曼树:一组带权的叶节点可以构造多个二叉树,其中WPL最小的树称为哈夫曼树或最优二叉树。
(4)假设哈夫曼树叶子节点的个数为m,则哈夫曼树的分支节点为m-1,总共节点个数为2m-1。
3.2 哈夫曼树的构造
哈夫曼树的构造:原则是将权值大的结点靠近根。根节点的值等于所有叶子节点的权值之和
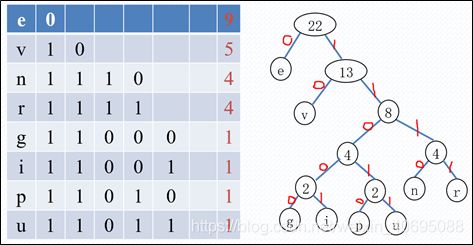
例子:用7,10,1,3,4,6,17构造一棵哈夫曼树
3.3 哈夫曼树编码
哈夫曼树编码:在哈夫曼树中把每个节点引向左孩子上的边标为0,引向右孩子的边标为1,再从上至下写出节点的编码
4、二叉树与树的转换
4.1树的表示方法
4.1.1父指针表示法
4.1.2孩子链表表示法
4.1.3孩子兄弟表示法
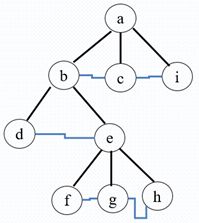
增加两个分别指向该结点的第一个孩子结点和下一个兄弟结点的指针,即左分支存放孩子节点,有分支存放兄弟节点
4.2树与二叉树的转换
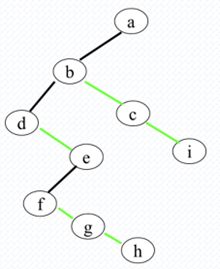
4.2.1树转为二叉树
1、树中同一结点的兄弟相连;
2、保留结点的最左孩子连线,删除其它孩子连线;
3、调整位置;
4.2.2二叉树转为树
即把所有右孩子节点变为兄弟节点
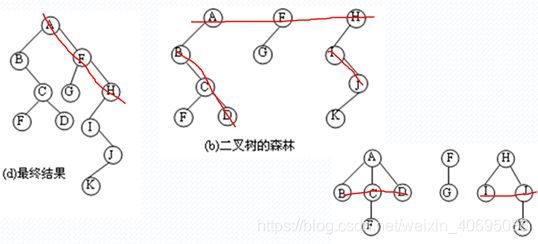
4.2.3森林转为树
森林中各树先各自转为二叉树;依次连到前一个二叉树的右子树上
4.2.4树转为森林
沿着右孩子链搜索,把所有右孩子连线去掉;把得到的每棵二叉树转换为树
5、二叉树与哈夫曼树操作代码(C语言)
(1)二叉树的顺序存储与周游
//二叉树的建立与基本操作
#include
#include
#define maxsize 20
//顺序存储的二叉树
typedef struct binarytree //定义一个顺序存储的节点数据类型,包含节点的个数和值
{
int data[maxsize]; //必须预定定义一个数组的大小存放节点的值
int nodenum; //记录节点的个数
}*Pbinarytree; //定义一个节点数据的指针类型
//创建一个空节点
Pbinarytree createNulltree() {
Pbinarytree tree1 = (Pbinarytree)malloc(sizeof(struct binarytree)); //创建一个空树
if (tree1 !=NULL)
tree1->nodenum = 0; /*空表长度为0 */
else
printf("Out of space!\n"); /*存储分配失败*/
return tree1 ;
}
int rootsnode(Pbinarytree t) { //求根节点的值
return t->data[0];
}
int parent(Pbinarytree t, int p) { //求二叉树t中右子节点p的双亲节点的值
if(p<0||p>=t->nodenum) return -1;
return (p-1)/2 ;
}
int lefchild(Pbinarytree t, int p) { //求二叉树t中节点p的左子节点的值
if(p<0||p>=t->nodenum) return -1;
return 2*p+1 ;
}
int rightchild(Pbinarytree t, int p) { //求二叉树t中节点p的右子节点的值
if(p<0||p>=t->nodenum) return -1;
return 2*p+2;
}
int insert(Pbinarytree palist, int p, int x) { //在树palist上的p节点位置放入元素值n
int q;
if ( palist->nodenum ==maxsize ) { /* 溢出 */
printf("Seq-list overflow!\n");
return 0;
}
if ( p < 0 || p > palist->nodenum ) { /* 不存在下标为p的元素 */
printf("Index of seq-list is out of range! \n");
return 0;
}
for(q = palist->nodenum - 1; q >= p; q--) /* 插入位置及之后的元素均后移一个位置 */
palist->data[q+1] = palist->data[q];
palist->data[p] = x; /* 插入元素x */
palist->nodenum++; /* 元素个数加1 */
return 1;
}
int main(){
Pbinarytree tree ;
int x;
int i;
tree=createNulltree();
for (i=0;i<6;i++)
{
scanf("%d",&x);
insert(tree,i,x);
}
printf("%d\n",rootsnode(tree));
printf("%d\n",parent(tree, 5));
} (2)二叉树的链式存储与周游
#include
#include
typedef char DataType;
struct BinTreeNode;
typedef struct BinTreeNode *PBinTreeNode;
struct BinTreeNode {
DataType info;
PBinTreeNode llink;
PBinTreeNode rlink;
};
typedef struct BinTreeNode *BinTree;
typedef BinTree *PBinTree;
typedef PBinTreeNode BNode;
PBinTreeNode root_btree(PBinTree t) {
return *t;
}
PBinTreeNode leftChild_btree (PBinTreeNode p){
return p->llink;
}
PBinTreeNode rightChild_btree (PBinTreeNode p){
return p->rlink;
}
PBinTreeNode createRest_BTree() { /* 递归创建从根开始的二叉树 */
PBinTreeNode pbnode;
char ch;
scanf("%c",&ch);
if ( ch == '@') pbnode = NULL;
else {
pbnode = (PBinTreeNode )malloc(sizeof(struct BinTreeNode));
if (pbnode == NULL) {
printf("Out of space!\n");
return pbnode;
}
pbnode->info = ch;
pbnode->llink = createRest_BTree();
pbnode->rlink = createRest_BTree();
}
return pbnode;
}
PBinTree create_BTree( void ) {
/* 创建完整的二叉树 */
PBinTree pbtree = (PBinTree)malloc(sizeof(BinTree));
if (pbtree != NULL)
*pbtree = createRest_BTree( ); /* 递归创建从根开始的二叉树 */
return pbtree;
}
void visit(BNode p) { printf("%c ",p->info); }
void inOrder(BNode p) { //中序访问
if (p == NULL) return;
inOrder(leftChild_btree(p));
visit(p);
inOrder(rightChild_btree(p));
}
void postOrder(BNode p) { //后序访问
if (p == NULL) return;
postOrder(leftChild_btree(p));
postOrder(rightChild_btree(p));
visit(p);
}
void prerder(BNode p) { //先序访问
if (p == NULL) return;
visit(p);
prerder(leftChild_btree(p));
prerder(rightChild_btree(p));
}
int main(){
PBinTree tree = create_BTree();
printf("中序访问 :");
inOrder(*tree);
putchar('\n');
printf("后序访问:");
postOrder(*tree);
putchar('\n');
printf("先序访问 :");
prerder(*tree);
putchar('\n');
return 0;
} (3)哈夫曼树的操作
/* huffman树的构造方法*/
#include
#include
#include
#define MAXINT 2147483647
#define MAXNUM 50 /* 数组w中最多容纳的元素个数,注意 m<=MAXNUM */
#define MAXNODE 100 /* 哈夫曼树中的最大结点数,注意 2*m-1ht[i].llink = -1;
pht->ht[i].rlink = -1;
pht->ht[i].parent = -1;
if (i < m)
pht->ht[i].ww = w[i];
else
pht->ht[i].ww = -1;
}
for ( i = 0; i < m-1; i++) {/* 每循环一次构造一个内部结点 */
m1 = MAXINT;
m2 = MAXINT;/* 相关变量赋初值 */
x1 = -1;
x2 = -1;
for (j = 0; j < m+i; j++) /* 找两个最小权的无父结点的结点 */
if (pht->ht[j].ww < m1 && pht->ht[j].parent == -1) {
m2 = m1;
x2 = x1;
m1 = pht->ht[j].ww;
x1 = j;
}
else if (pht->ht[j].ww < m2 && pht->ht[j].parent == -1) {
m2 = pht->ht[j].ww;
x2 = j;
}
pht->ht[x1].parent = m+i; /* 构造一个内部结点 */
pht->ht[x2].parent = m+i;
pht->ht[m+i].ww = m1+m2;
pht->ht[m+i].llink = x1;
pht->ht[m+i].rlink = x2;
pht->root = m+i;
}
return pht;
}
int main() {
char str[20];
int i1,num[256]={0},k=0;
printf("please input a string: ");
scanf("%s",str);
for(i1=0;i1ht[i].parent != -1) {
parent = pht->ht[i].parent;
if (pht->ht[parent].llink == i)
printf("0");
else
printf("1");
i = parent;
}
printf("\n");
}
return 0;
}