计算机基础--进制之间的转换
前言
在学习计算机时，不可避免是需要了解进制的概念以及它们之间是如何进行转换的。
一. 进制的介绍
1.1 概念介绍
二进制的概念：
二进制是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数。它的基数为2，进位规则是“逢二进一”，借位规则是“借一当二”，计算机中的二进制则是一个非常微小的开关，用1来表示“开”，0来表示“关”。
八进制的概念：
八进制，Octal，缩写OCT或O，一种以8为基数的计数法，采用0，1，2，3，4，5，6，7八个数字，逢八进1。一些编程语言中常常以数字0开始表明该数字是八进制。八进制的数和二进制数可以按位对应(八进制一位对应二进制三位)，因此常应用在计算机语言中。
十六进制的概念：
十六进制(英文名称:Hexadecimal)，是计算机中数据的一种表示方法。同我们日常生活中的表示法不一样。它由0-9，A-F组成，字母不区分大小写。与10进制的对应关系是:0-9对应0-9;A-F对应10-15;N进制的数可以用0~(N-1)的数表示，超过9的用字母A-F。
十进制的概念：
十进制实际上是全世界通用的进制语言，1,2，3,4，逢9进1…
1.2 进制的表现方式
对于进制，有四种表现方式
1. 二进制：0,1 ，满2进1
2. 十进制：0-9，满10进1
3. 八进制：0-7 ，满8进1，以数字0开头表示
4. 十六进制：0-9及A-F，满16进1，以0X或0X开头表示
| 十进制 | 十六进制 | 八进制 | 二进制 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 |
| 8 | 8 | 10 | 1000 |
| 9 | 9 | 11 | 1001 |
| 10 | A | 12 | 1010 |
| 11 | B | 13 | 1011 |
| 12 | C | 14 | 1100 |
| 13 | D | 15 | 1101 |
| 14 | E | 16 | 1110 |
| 15 | F | 17 | 1111 |
| 16 | 10 | 20 | 10000 |
| 17 | 11 | 21 | 10001 |
二. 进制的转换
进制的转换这里分为四组依次介绍转换的规则和演示
第一组（其他进制转十进制）
二进制转十进制
八进制转十进制
十六进制转十进制
第二组(十进制转其他进制)
十进制转二进制
十进制转八进制
十进制转十六进制
第三组（二进制转其他进制）
二进制转八进制
二进制转十六进制
第四组（其他进制转二进制）
八进制转二进制
十六进制转二进制
2.1 第一组（其他进制转十进制）
2.1.1 二进制转十进制
规则：从最低位开始（最右边），将每个位上的数提取出来，乘以2的（位数-1）次方，然后相加求和。
演示：
110010=0*2+1*2+0*2*2+0*2*2*2+1*2*2*2*2 +1*2*2*2*2*2 = 50
可能一下子不是那么容易看出来，这里再举一个例子：
二进制 111 ，将它转成十进制
从右边开始，每位数*2（位数-1）次方
111 = 1 * 2的0次方 ==>2的0次方也就是1 + 1 * 2的1次方 + 1 * 2的2次方= 1+ 2+4 =7
因此111转成十进制等于数字7
可以使用计算器做下验证，点击计算器的查看再点击程序员那一栏就到这个位置了
二进制页面输入111后，然后在点击十进制后，就会显示对应的值了，可以看到结果是7。
2.1.2 八进制转十进制
规则：从最低位开始（最右边），将每个位上的数提取出来，乘以8的（位数-1）次方，然后相加求和。
演示：
0777 = 7 * 1 + 7 * 8 + 7 * 8 * 8 = 511
还是一样的方式，只不过这回是乘以8。
2.1.3 十六进制转十进制
规则：从最低位开始（最右边），将每个位上的数提取出来，乘以16的（位数-1）次方，然后相加求和。
演示：
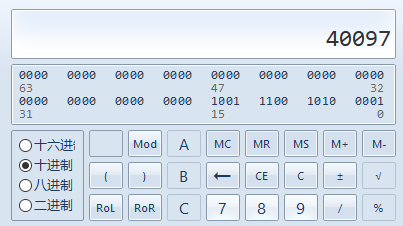
0X9CA1 = 1 * 1 + 10 * 16 + 12 * 16 * 16 + 9 * 16 * 16 * 16 = 40097
前面0X是十六进制的固定写法，16进制要转换的内容是9CA1。
计算出来可以看到十六进制转十进制的数还是特别大的。
2.2 第二组(十进制转其他进制)
2.2.1 十进制转二进制
规则：将该数不断除以2，直到商为0为止，然后将每步得到的余数倒过来，就是对应的二进制。
演示：
比如有一个十进制的数字是56，将它转成二进制是需要不断将这个数除以2，直到不能被2整数；而后将每步得到的余数倒过来，就会得出二进制的数值。
如下图，整个流程计算下来，十进制转二进制的数值是111000。
2.2.2 十进制转八进制
规则：将该数不断除以8，直到商为0为止，然后将每步得到的余数倒过来，就是对应的八进制。
演示：
比如有一个十进制的数字是160，将它转成八进制是需要不断将这个数除以8，直到不能被8整数；而后将每步得到的余数倒过来，就会得出八进制的数值。
如下图，整个流程计算下来，十进制转八进制的数值是0240。
2.2.3 十进制转十六进制
规则：将该数不断除以16，直到商为0为止，然后将每步得到的余数倒过来，就是对应的十六进制。
演示：
比如有一个十进制的数字是350，将它转成十六进制是需要不断将这个数除以16，直到不能被16整数；而后将每步得到的余数倒过来，就会得出十六进制的数值。
如下图，整个流程计算下来，十进制转十六进制的数值是0X15E。
还记得为什么14是E吗，因为十六进制超过9以后是以字母A-F表示的。
2.3 第三组（二进制转其他进制）
2.3.1 二进制转八进制
规则：将二进制数每三位一组（从低位开始组合），转成对应的八进制数即可。
演示：
1010011
将二进制数分成三位一组，从右开始，若不够三位的可以在前面补0 ；即 001 010 011
还记得二进制是怎么算的吗，逢2进1的方式
结果是 1 2 3。
2.3.2 二进制转十六进制
规则：将二进制数每四位一组（从低位开始组合），转成对应的十六进制数即可。
11101101
将二进制数分成四位一组，从右开始，若不够四位的可以在前面补0 ；即 1110 1101
结果是 0XED。
2.4 第四组（其他进制转二进制）
2.4.1 八进制转二进制
规则：将八进制的每一位，转成对应的一个3位的二进制数即可，从右往左开始。
演示：
0403
将每一位八进制的数都转成对应的三位的二进制
3对应三位的二进制是 011
0对应三位的二进制是 000
4对应三位的二进制是100
拼起来就是 100000011
2.4.2 十六进制转二进制
规则：将十六进制的每一位，转成对应的一个4位的二进制数即可，从右往左开始。
演示：
0X1AE
将每一位十六进制的数都转成对应的四位的二进制
E对应四位的二进制是 1110
A对应四位的二进制是 1010
1对应四位的二进制是 0001
一起就是000110101110 ，而前面的0可以不写即110101110
总结
进制之间的转换内容就是这么多，学习进制的同时也能加深对计算机的理解，若觉得内容还行的，可以点赞支持一下！
