864.获取所有钥匙的最短路径（BFS+位图技巧）

864. 获取所有钥匙的最短路径 

给定一个二维网格 grid ，其中：

• '.' 代表一个空房间
• '#' 代表一堵
• '@' 是起点
• 小写字母代表钥匙
• 大写字母代表锁  

我们从起点开始出发，一次移动是指向四个基本方向之一行走一个单位空间。我们不能在网格外面行走，也无法穿过一堵墙。如果途经一个钥匙，我们就把它捡起来。除非我们手里有对应的钥匙，否则无法通过锁。

假设 k 为 钥匙/锁 的个数，且满足 1 <= k <= 6，字母表中的前 k 个字母在网格中都有自己对应的一个小写和一个大写字母。换言之，每个锁有唯一对应的钥匙，每个钥匙也有唯一对应的锁。另外，代表钥匙和锁的字母互为大小写并按字母顺序排列。

返回获取所有钥匙所需要的移动的最少次数。如果无法获取所有钥匙，返回 -1 。

示例 1：

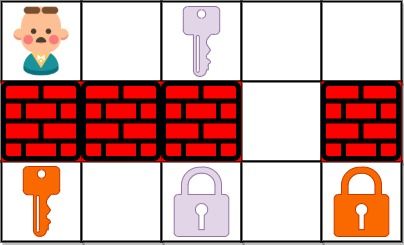
输入：grid = ["@.a.#","###.#","b.A.B"]
输出：8
解释：目标是获得所有钥匙，而不是打开所有锁。

示例 2：

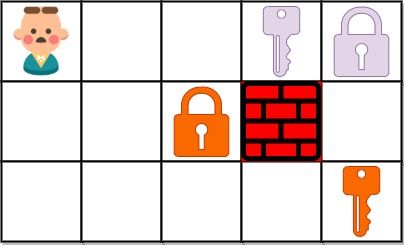
输入：grid = ["@..aA","..B#.","....b"]
输出：6

示例 3:

输入: grid = ["@Aa"]
输出: -1

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 30
• grid[i][j] 只含有 '.', '#', '@', 'a'-'f' 以及 'A'-'F'
• 钥匙的数目范围是 [1, 6] 
• 每个钥匙都对应一个 不同 的字母
• 每个钥匙正好打开一个对应的锁

思路：BFS+状态压缩（位图）

首先，遇到二维数组的BFS，应该用queue队列存放每个点的坐标(x, y)作目前状态，用二维数组dire={{-1,0},{1,0},{0,-1},{0,1}}作上下左右四个方向的选择。此外，还需要使用二维数组visited记录已经遍历过的点，防止走回头路，未遍历的记作visited[x][y]=false,遍历过的记作visited[x][y]=true,类似题目见934. 最短的桥 - 力扣（LeetCode）

 但是这道题中，是可以走回头路的，这取决于你拿到钥匙的状态。如果例一中，第一行的钥匙在最后一格，那么为了拿到所有的钥匙，就要先向右走到头，再向左走从两堵墙中间下去，这就走了回头路。

所以visited数组应该是一个三维数组，包括了该点的坐标以及此时拿到钥匙的状态，意为该点(x, y) 是可以重复经过的，但是重复经过时拿到钥匙的状态应该有所不同。

visited(m,vector>(n,vector(allkey+1,false)))

同理，压入队列中的每一种状态也应该是该点的坐标(x, y)+拿到钥匙的状态

struct State {
    int x;
    int y;
    int key;   
};

我们使用int key 来表示拿到钥匙的状态，key的二进制表示为1010时，表示拿到第2把和第4把钥匙。下列是一些有用的位图技巧：

1、将第m位置1   (m>=1)                          key | = 1<< (m-1)                                                            

2、判断第m位是否是1    (m>=1)              ( key >> (m-1) ) & 1) ==0 时不为1 ，==1 时为1

struct State {
    int x;
    int y;
    int key;
};
class Solution {
public:
    int shortestPathAllKeys(vector& grid) {
        State start;
        int keycnt=0;
        int m=grid.size();
        int n=grid[0].size();
        queue q;
        vector> dire={{-1,0},{1,0},{0,-1},{0,1}};
        for(int i=0;i='a'&&grid[i][j]<='z')//记录钥匙数
                {
                    keycnt++;
                }
            }
        }
        q.push(start);//初始状态入队
        int allkey=(1<>> visited(m,vector>(n,vector(allkey+1,false)));
        //visited数组，记录遍历过程中的状态，防止走回头路。(“状态”是指在点(x,y)处拥有钥匙的状态)
        int step=0;
        while(!q.empty())
        {
            int size=q.size();
            for(int i=0;i=m||y>=n)//越界
                        continue;

                    char c=grid[x][y];
                    if(c=='#')//墙
                        continue;

                    if(c>='A'&&c<='Z')//遇到锁
                    {
                        //遇到锁'B',判断有无钥匙'b',即判断key的第二位是否为1
                        //将要判断的那位移到末尾，再与001相与，为000，则该位是0，为001，则该位是1
                        if((key>>(c-'A')&1)==0)//若key=1001,则1001>>('B'-'A')=0100,0100&0001=0000,没有'b'钥匙
                        {
                            continue;
                        }
                    }

                    if(c>='a'&&c<='z')//捡到钥匙
                    {
                        //更新钥匙状态
                        key |=1<<(c-'a');//若得到钥匙'b',则1<<('b'-'a')是二进制的10,key与10相或，就将第二位置1
                    }

                    if(visited[x][y][key]==true)//已经遍历过
                        continue;

                    visited[x][y][key]=true;//更新已遍历过的情况
                    //将情况加入队列中
                    q.push(State{x,y,key});//C++11新语法，数据类型后面直接加{},给成员变量赋初值
                }
            }
            step++;
        }
        return -1;
    }
};