火箭参数相关知识
火箭参数相关
前言:学习笔记,很初级部分内容来之相关书籍,入门学习,欢迎指正
1 坐标系右手定则:
伸开手掌,大拇指指向X轴,四指指向Y轴,四指弯曲90°后所指向的方向为Z轴。X 、Y、Z并没有约定产生的顺序,所以实际应用你也可能知道X 轴、Z轴来确定Y轴方向。
2 火箭转序:
使用的321转序,即箭体坐标系的Z->Y->X也就是俯仰、偏航、滚动转序
3 太阳同步轨道:
通俗点就是太阳光线和卫星轨道面的夹角始终为固定角度的轨道,运算上就是使卫星由于地球非圆形导致的卫星轨道面自转的角速度等于地球绕太阳公转的角速度,从而使得太阳光线和卫星轨道面的夹角始终保持一致。可见个人文档《太阳同步轨道学习笔记》。
4 火箭发射相关的坐标系:
3.1 发射系(发射坐标系):
O点为发射点,Y轴为发射点铅垂线(重力方向)的反方向为正Y,X轴为发射瞄准方向(是发射的目标方向所在面且与Y轴垂直的方向),Z轴与X Y遵循右手定则。其中,X轴与正北向的夹角叫做方位角(方位角是以发射时刻判定的未考虑地球自转的方位)。(由于地球不是正圆,所以Y轴的铅垂线方向并不指向地心)。
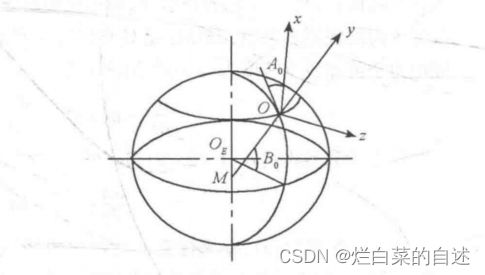
火箭垂直发射,发射系的X轴和箭体的X轴(箭体坐标系)相差90°,并不重合。
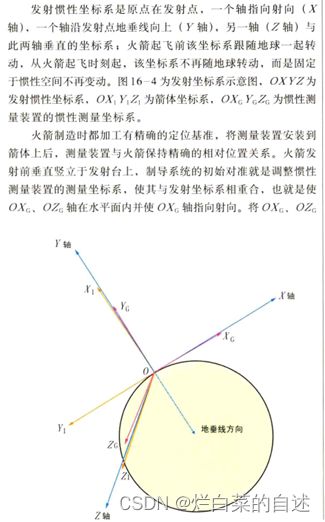
3.2 发惯系(发射惯性系):
以火箭发射点为原点,在起飞瞬间与发射坐标系各轴重合,起飞后,惯性坐标系的各轴方向在惯性空间保持不变。(注意:发惯系只有在起飞的时刻才建立,起飞之前的箭体姿态信息都是相对于发射系的,所以会看到射前针对发射系做的比如综测项目和飞控起飞前惯组陀螺输出数据要刨除地速,而起飞后由于惯组自身为惯性器件,不在地球上不存在地速(相对发惯系),姿态相对发惯系而言的,如果姿态角保持不变,理论上惯组输出角速度应该为0)
3.3 惯组测量坐标系:
惯组自身输出的测量数据对应的坐标系,我们在惯组安装时,一般把惯组和箭体系方向保持一致(惯组测量坐标系和箭体坐标系位置保持一致,其也是非惯性坐标系,所以实际各轴输出是转换后的),这样就少一个坐标系的转换,但是惯组测量坐标系的原点是安装位置,而箭体系原点是质心。这样我们姿控控制时就以惯组测量坐标系来进行实际的控制(实际来说应该是箭体系)。
3.4 箭体系(箭体坐标系,又称本体坐标系):
我们飞控使用的象限轴、和姿态控制的俯仰、偏航、滚动控制都是针对箭体系的,姿控的控制也都是在箭体系下来控制的。(火箭说的象限实际上是象限轴,而不是数学学的一个90°区域)。
象限线:是指箭体系OYZ平面内,Y轴正向为III象限轴(-Y为I象限轴),Z轴正向为IV象限(-Z为II象限轴)。
箭体惯组安装位置为惯组测量坐标系的原点(诸元中高程说的是惯组安装位置的高度),X轴为火箭外壳对称轴,指向箭体的头部,Y轴是与X轴对称且在发射瞬间与发射系xoy平面内的轴(如果地面绝对水平),Z轴由右手坐标系确定。
(注意:书本定义箭体坐标系坐标原点是火箭的质心,我们火箭实际使用时并不是以质心为坐标原点,而是以惯组所在安装位置为坐标原点,质心在运动飞行过程中会伴随质量和各级分离逐渐变化,而质心的变化在发射前已经估算出来了并且在飞行过程中对数据进行了对应比例积分补偿,也就是说我们实际用的箭体坐标系和书本定义的箭体坐标系原点是有差异的)。
3.5 地固系(又称地球固联坐标系):
坐标系的原点Oe在地球质心,OeZe指向地球自转角速度矢量方向(即北极),垂直于赤道平面;OeXe在赤道平面内指向格林尼治子午线;OeYe轴和OeZe、OeXe轴构成右手坐标系。根据参考历元与椭球模型不同,应用不同标准给定的数据,如WGS84,CGCS2000等。我们的GNSS数据数据就是以地固系进行的数据输出。
判断伺服各方向分力注意力是空间三个轴方向分力
5 加速度计原理:
加速度计的敏感原理是外部作用力使得加速度计中的敏感器件产生形变对应输出数据,所以这里的重点是注意敏感的受外力。加速度计测得的数据并不包含重力加速度,比如空中自由落体的物体,加速度计输出为0,因为没有受到外力。而在桌面放着测试加速度计输出实际是外力(支持力)的作用值。故加速度计输出的加速度值称为视加速度(所谓视加速度就是不包含重力加速度以外的加速度)。加速度计是用来测量视加速度的工具。
既然加速度计得到的是视加速度,所以火箭真正飞行的加速度就需要加速度计的视加速度加上所在位置的等效重力加速度得到实际的加速度值。
制导是针对质点运行的控制,关心的是速度和位置(加速度计),质心运动的控制是靠改变火箭俯仰、偏航姿态角实现的。姿控针对的是姿态俯仰偏航滚动的控制,关心的是角速度(速率陀螺为姿态敏感型器件)。
姿控对姿态的控制为超前控制(但是是在矫正网络中实现,综测不涉及)。
我们说姿态角的潜在含义就是说的姿态在当前参考系相对于另一个参考系而言的,不存在绝对的某个坐标系的姿态。(姿控使用的姿态角就是箭体系相对于发惯系的姿态)
6 姿态角偏差:
火箭的姿态角随着飞行弹道的变化是实现设计好的,称作程序角。然而,飞行过程中的一些随机因素,比如风干扰、结构干扰等会使得姿态角偏离预定值,将实际的飞行姿态角与程序角(理论的姿态角)相减得到的值即称为姿态角偏差。
7 脱插脱拔:
脱插插头和脱拔插头都是箭上使用地供电源供电时的连接插头,脱拔插头是安装在火箭尾部与地面发射控制系统连接的插头,该插头靠火箭起飞时拔动其芯杆而脱落,所以称为脱拔插头。脱落插头是通过电控断开。
8 初始对准和光瞄(光学瞄准)的关系:
从功能上讲,初始对准和光学瞄准都是用来测量惯性测量坐标系(因为惯性测量坐标系和箭体坐标系一般认为是一致的,所以也可以认为是箭体坐标系)和发射系(就是选取参考系,也可能是地固系)的坐标系夹角转换关系,两者功能是一样的。从精度上讲,光瞄的精度更高,因为选用了更高精度的陀螺来标定,而初始对准使用的是火箭自身的惯组用来标定(初始对准不借助外部设备,使用惯组数据测量,光瞄:使用激光进行瞄准)。从流程上讲,软件总检查都会有初始对准的测量,而光瞄只是在真正火箭(真正起竖)发射前做一次。从型号上讲,Y1、Y2做初始对准数据但是实际并没有使用对应的结果,因为有光瞄,而Y3取消了光瞄,因此使用初始对准数据作为输入。
光瞄从工作流程上讲大致报货标定4、粗瞄、精瞄三步。
9 姿控系统极性检查:
(姿控系统极性检查属于射前项目,发惯系未建立,所以姿控的控制是相对于发射系而言的,这就是为什么要刨除地球自转角速度分量的原因
9.1 初始化四元数、姿态角、程序角
依据任务书要求配置初始四元数、姿态角、程序角(程序角初值为0,即不存在角偏差);(软件其实没必要四元数由姿态转换矩阵进行反推,直接给初值就行)
扩展:由四元数计算出的姿态转换矩阵是通用公式,是唯一的,而由欧拉角不同的转序(3次转动)算出的与姿态角的关系是不同的,不同的转序对应姿态角不同。比如321转序下某个俯仰角90°,而312转序俯仰角可能是0°。
9.2 地球自转角速度与陀螺实际有效输出分量计算
- 由于陀螺在箭体系下的输出是包含地球自转角速度的,因此先计算出陀螺在箭体系下的各轴地球自转角速度分量。地球自转角速度先分解到发射系下比较容易,所以先将地球自转角速度在发射系下的各轴分量进行分解。其分解到三个轴(X Y Z)的方向余弦矩阵如下:其中 代表射向(发射方位角), 代表发射点纬度。
由上述方向余弦矩阵乘以地球自转角速度得到发射系下地球各轴自转分量。
接下来,发射系下地球自转角速度分量乘以发射系到箭体系的姿态转换矩阵 ,即得到箭体系下的地球自转角速度分量。
9.3 进入周期性运算
下属1)-6)属于导航制导解算,7)-9)属于姿控控制
-
周期性采集惯组(或陀螺数据),获得当前周期的陀螺输出的各轴角度增量和视速度增量(箭体系下)。
当前周期箭体系下火箭的角度增量按照下属公式获得,其中T1为控制周期。 -
计算角速度:由于角增量/周期并不是准确的代表本周期起始时刻的角速度,这里计算角速度公式用的是(3.0Cur-Lst)/(2.0T1),其中Cur为当前周期的角增量,Lst为上一周期的角增量,T1为控制周期。(这部分任务书也没有体现,属于没有出处),具体机理如下:认为角增量属于线性曲线,如下图。
当周期收到的惯组数据解算后得到的角增量实际是上一个5ms的增量,Cur/T得到速度均值(也就是上一个周期中间时刻的角速度),Lst/T得到速度均值(也就是上上一个周期中间时刻的角速度),由线性比例得到点3也就是当前运行周期起始点的速度值:
Cur/T +( (Cur/T- Lst/T)/T)(T/2) = (3.0Cur-Lst)/(2.0*T1)。 -
有角增量(在发射系下)得到对应的四元数
-
由四元数得到对应的姿态转换矩阵
-
由姿态转换矩阵得到箭体系相对于发射系的姿态角
-
姿态偏差解耦:箭体坐标系的三个轴是随着箭体的滚动随之变化的(而不是固定指向),姿态偏差解耦的目的就是当箭体滚转后,箭体的三个轴方向随之改变,得到真正的箭体滚动后要控制的姿态角。(比如,本身姿态角偏差俯仰和滚动非零,如果滚动非0情况下只需要控制俯仰就行了,此时滚动非零,箭体的X Y轴方向就改变了,就不能通过控制原来本身的俯仰来实现了),下面的公式2就是算出有滚动的情况下实际箭体要进行的控制动作。
其中:
分别为制导给出的俯仰、偏航、滚动程序角;
为解耦后箭体坐标系下的姿态角偏差。
7) 伺服控制:
分别为摆动喷管比例、微分增益系数;Dtest为进行转台滤波综测专门加的滤波系数。(实际的微分就是求导)。得到姿态控制摆角指令
sat为矢量限幅,得到安全的限幅输出。 为总摆角限幅值;
分配到伺服A B作动器上为:
- 俯仰偏航RCS控制:
分别为末修RCS比例、微分增益系数; 分别为俯仰、偏航通道RCS控制反馈;
RCS控制借助斯密特触发器进行解算具体结果,得到 分别为俯仰、偏航通道RCS控制指令。
译码算法key=( +1)*9+( +1)*3+( +1)*1,得到键值。然后由键值得到对应的译码表控制指令。
9) 滚控控制:一级滚控和RCS姿控喷管滚控使用的算法相同
为滚动通道RCS控制反馈, 分别为滚动控制比例、微分增益系数
滚控均借助斯密特触发器进行解算具体结果,得到 为滚动通道RCS控制指令, 分别为滚动控制开、关门限。
根据滚动RCS控制指令 ,查表给出滚控装置各个电磁阀的动作指令。