Matplotlib绘图（2）——散点图

Matplotlib绘图

本内容主要介绍了Matplotlib库可以绘制的图形，即实现数据可视化。
本内容仅为我个人的学习总结。

1 散点图：

散点图是利用坐标点的分布形态反映特征间的相关关系的一种图形。这里的散点图均为二维散点图，可通过点的疏密程度和变化趋势表示两特征间的关系。

个人绘图经验：

• 使用散点图绘制的数据一般为离散型的数据
• 可通过绘制散点图查看特征之间是否存在关联趋势，即线性还是非线性
• 可通过绘制散点图查看是否有离群点（异常值）
• 也可通过绘制散点图查看不同标签的特征分布情况（语言组织可能会有点混乱，下面绘图会提到）

使用语法如下：

matplotlib.pyplot.scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, verts=None, edgecolors=None, hold=None, data=None, **kwargs)

参数说明：

参数	说明
x, y	array, 表示x轴和y轴对应的数值，无默认值
s	一维的array或数值，指定点的大小，若为一维array则表示每个点的大小，默认为None
c	颜色或是一维array，指定点的颜色，若为一维array则表示每个点的颜色，默认为None
marker	特定的str，表示点的类型，有规定哪个字符串为哪个类型，默认为None
alpha	0-1的小数，表示点的透明度，默认为None

1 简单绘制一张图表：

import matplotlib.pyplot as plt 
import numpy as np
# 构建数据
x = np.linspace(0, 2*np.pi,100) # [0:2π]取100个点
y = np.sin(x) + 2
y2 = np.cos(x) - 2
# 绘制一张图表
plt.rcParams['font.sans-serif'] = 'SimHei'  # 正常显示中文
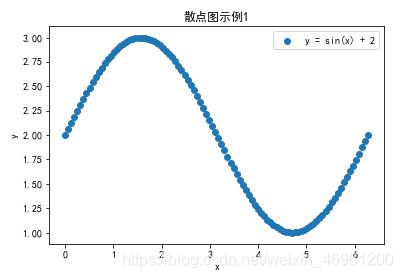
plt.title('散点图示例1')  # 添加标题
plt.xlabel('x') # 添加x轴标签
plt.ylabel('y') # 添加y轴标签
plt.scatter(x, y) # 绘制散点图
plt.legend(['y = sin(x) + 2']) # 添加图例
# plt.savefig('散点图示例1.jpg') # 保存图表
plt.show()

绘图结果：

2 同一张图表简单绘制多个图

plt.rcParams['font.sans-serif'] = 'SimHei'  # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
plt.title('散点图示例2')  # 添加标题
plt.xlabel('x') # 添加x轴标签
plt.ylabel('y') # 添加y轴标签
plt.xlim(-1, 7) # 设置x轴刻度范围
plt.ylim(-4,4) # 设置y轴刻度范围
plt.scatter(x, y) # 绘制散点图
plt.scatter(x, y2)
plt.legend(['y = sin(x) + 2', 'y2 = cos(x) - 2']) # 添加图例
# plt.savefig('散点图示例2.jpg') # 保存图表
plt.show()

结果显示：

3 同一个画布简单绘制两个图表

plt.rcParams['font.sans-serif'] = 'SimHei'  # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号

plt.subplot(2,1,1)# 将画布划分成两行一列，取第一个放第一个图表内容
plt.scatter(x, y, c = 'r') # 绘制散点图
#对子图添加亿点点
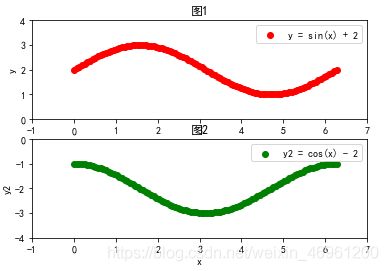
plt.title('图1')  # 添加标题
plt.xlabel('x') # 添加x轴标签
plt.ylabel('y') # 添加y轴标签
plt.xlim(-1, 7) # 设置x轴刻度范围
plt.ylim(0,4) # 设置y轴刻度范围
plt.legend(['y = sin(x) + 2']) # 添加图例

plt.subplot(2,1,2) # 将画布划分成两行一列，取第二个
plt.scatter(x, y2, c = 'g')
#对子图添加亿点点
plt.title('图2')  # 添加标题
plt.xlabel('x') # 添加x轴标签
plt.ylabel('y2') # 添加y轴标签
plt.xlim(-1, 7) # 设置x轴刻度范围
plt.ylim(-4, 0) # 设置y轴刻度范围
plt.legend(['y2 = cos(x) - 2'])# 添加图例

# plt.savefig('散点图示例1.jpg') # 保存图表
plt.show()

结果显示：

图中的数据x和y是有一定的线性关系的，通过绘制x和y的散点图，可以很明显地看出他们之间的线性关系。

对于线性关系没有那么强的数据，也是可以通过绘制散点图查看数据大概的走向或趋势，以及对比不同数据之间走向或趋势

4 导入数据绘制一张图表

#使用scatter函数绘制2000~2017年各季度的国民生产总值散点图

import matplotlib.pyplot as plt 
import numpy as np 
data = np.load('H:/1-大四学习资料/python可视化/Matplotlib绘图/国民经济核算季度数据.npz',allow_pickle=True) 
name = data['columns']  # 提取columns数组，视为数据的标签 
values = data['values']  # 提取values数组，数据的存在位置 

plt.rcParams['font.sans-serif'] = 'SimHei' # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
plt.figure(figsize = (8, 7)) # 设置画布大小
plt.scatter(values[: ,0], values[: , 2], marker = 'o') # marker='o'设置点的形状为圆形
plt.xlabel('年份') # 添加x轴标签
plt.ylabel('生产总值（亿元）') # 添加y轴标签
plt.xticks(range(0, 70, 4), values[range(0, 70, 4), 1], rotation = 45) # 设置x轴刻度，rotation = 45, x轴刻度旋转45度
plt.title('2000~2017年季度生产总值散点图') 
#plt.savefig('../tmp/2000~2017年季度生产总值散点图.png') 
plt.show() 

结果显示：

可以看出2000~2017年季度生产总值大概呈向上的趋势发展，即人们的生产总值越来越高

5 同一个图表绘制多个图，并比较不同图之间的关系

#绘制2000~2017年第一产业、第二产业、第三产业各季度的国民生产总值散点图
plt.Figure(dpi = 80, figsize = (8, 7)) 
plt.rcParams['font.sans-serif'] = 'SimHei' 
# 第一产业
y1 = values[: , 3] 
plt.scatter(range(len(y1)), y1) 
plt.xticks(range(len(y1)), values[: : 4, 1], rotation = 45) 
# 第二产业
y2 = values[: , 4] 
plt.scatter(range(len(y2)), y2) 
plt.xticks(range(len(y2)), values[: : 4, 1], rotation = 45) 
#第三产业
y3 = values[: , 5] 
plt.scatter(range(len(y3)), y3) 
plt.xticks(range(0, 70, 4), values[range(0, 70, 4), 1], rotation = 45) 

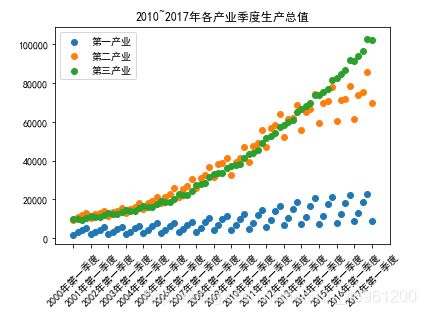
plt.title('2010~2017年各产业季度生产总值') 
plt.legend(['第一产业', '第二产业', '第三产业']) 
#plt.savefig('../tmp/三种产业散点图.png') 
plt.show()

结果显示：

从图可以看出，三个产业在2000年-2017年期间生产总值均呈上升趋势发展。第三产业和第二产业的发展趋势比第一产业的发展趋势好，上升速度也比第一产业快。第三产业和第二产业的上升的幅度非常接近，但在近两年第三产业的生产总值比第二产业的生产总值好。

从以上两个图来看，绘制散点图可以表现特征之间是否存在数值或是数量的变化或趋势， 也可对比不同特征之间的数量变化与趋势

6 绘制散点图查看不同标签的特征分布情况

这里使用的数据是鸢尾花数据

import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_iris

iris = load_iris()
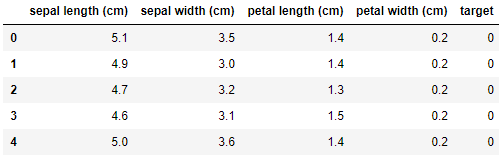
data = pd.DataFrame(iris.data,columns = iris.feature_names)
data['target'] = iris.target
data.head()

结果显示：

plt.rcParams['font.sans-serif'] = 'SimHei' #显示中文

d0 = data.loc[data['target'] == 0] # 提取标签为0的数据
d1 = data.loc[data['target'] == 1] # 提取标签为1的数据
d2 = data.loc[data['target'] == 2] # 提取标签为2的数据

# 散点图1：x为标签为0的花萼长度；y为标签为0的花瓣长度
x0 = d0['sepal length (cm)']; y0 = d0['petal length (cm)']
plt.scatter(x0, y0, color = 'b') # 绘制，颜色为蓝色
# 散点图2：x为标签为1的花萼长度；y为标签为1的花瓣长度
x1 = d1['sepal length (cm)']; y1 = d1['petal length (cm)']
plt.scatter(x1, y1, color = 'g') # 颜色为绿色
# 散点图3：x为标签为2的花萼长度；y为标签为2的花瓣长度
x2 = d2['sepal length (cm)']; y2 = d2['petal length (cm)']
plt.scatter(x2, y2, color = 'r') # 颜色为红色

plt.legend(['标签为0', '标签为1', '标签为2']) # 添加图标
plt.xlabel('花萼长度') # 添加x轴标签
plt.ylabel('花瓣长度') # 添加y轴标签
plt.show()

结果显示：

可以看到不同的标签特征分布情况不一样，而且他们所在的区域不一样的，如品种0的花瓣长度是三个品种中最短的，而花萼长度主要在5.0左右，品种3的花瓣长度是3个品种最长的，花萼长度也比其他品种长。

关于颜色和大小的补充：

一般来说，绘图大小 s 默认为20，s=0时点不显示；颜色 c 默认为蓝色。

• 大小 s 可以为一个数值，也可以是一维array
• 颜色 c 可以是指定的str(有规定)，也可是一维array

常用的颜色str指定的颜色如下：

str	颜色
b	蓝色
r	红色
g	绿色
m	紫色
y	黄色
c	青色
k	黑色
w	白色

大小和颜色为一维array：

import matplotlib.pyplot as plt
import numpy as np
x = [1,2,3,4,5,6,7]
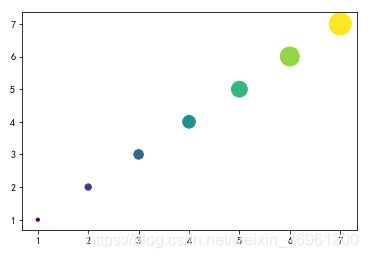
plt.scatter(x, x, s=10*np.array(x)**2, c=x)
plt.show()

结果显示：

在这里s = [100, 400, 900, 1600, 2500, 3600, 4900] 数值越大，点的大小就越大。
一维array的c中各数值表示的颜色，是在颜色带中按比例取得颜色。

颜色带：

色卡：

源于Matplotlib这部分，大家可以去下面这个网站查找相关内容，里面有很多资源和教程，有兴趣的小伙伴可以去看一下
Matplotlib中文网

文献参考：
[1] matplotlib中文网 https://www.matplotlib.org.cn/
[2]色卡图（他的图是真的好看，侵权删）https://www.jianshu.com/p/53ebc1c40258