【强化学习】时间差分法(TD)

引用 知乎专栏 天津包子馅儿的知乎

1、前言

之前的强化学习分类中介绍了几种强化学习方法的分类，今天就说一下其中重要的算法思想时间差分法，TD与蒙特卡罗法主要是在值函数的更新上有所差异，我们可以先看下图

动态规划法：
需要一个完全已知的环境，需要状态之间的转换概率，并且V(S)状态值函数的估计是自举的(bootstrapping)，即当前状态值函数的更新依赖于已知的其他状态值函数，也就是使用bellman方程求解值函数。

$V(s)\leftarrow E_{\pi }[R_{t+1}+\gamma V(s^{\prime })]$

此处有一个概念：值函数的计算用到了bootstapping的方法。所谓bootstrpping本意是指自举，此处是指当前值函数的计算用到了后继状态的值函数。即用后继状态的值函数计算当前值函数。

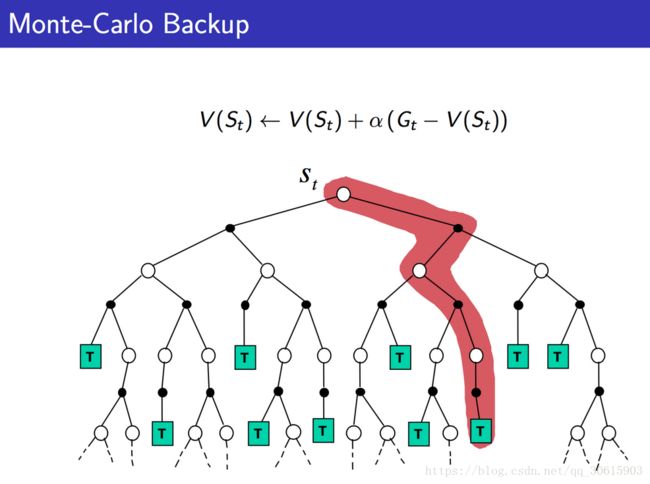
蒙特卡罗法：
我们之前在PolicyGradient中使用到了这种方法，他可以应用在model-free的算法中，但是他需要执行完整的一个episode的才可以进行估计。注意此处的$G_t$是利用经验平均估计状态的值函数所计算出来的。

$V(s)\leftarrow V(s)+\alpha (G_t-V(s))$

所以可以看出使用蒙特卡罗法需要回合结束才能更新，结合以上两者的优势就得到了TD算法

2、时间差分法TD

时间差分方法结合了蒙特卡罗的采样方法和动态规划方法的bootstrapping(利用后继状态的值函数估计当前值函数)使得他可以适用于model-free的算法并且是单步更新，速度更快。值函数计算方式如下

$V(s)\leftarrow V(s)+\alpha (R_{t+1}+\gamma V(s^{\prime })-V(s))$

其中$R_{t+1}+\gamma V(s^{\prime })$被称为TD目标，${\delta }_t=R_{t+1}+\gamma V(s^{\prime })-V(s)$ 称为TD偏差。
我们可以发现其实就是把蒙特卡罗法中估计的$G_t$替换成了TD目标，因为TD目标使用了bootstrapping方法估计当前值函数，所以这样就结合了动态规划的优点避免了回合更新的尴尬。
TD(0)的估计方式如下

TD(λ)可以通过在TD-target再根据bellman方程展开，就可扩展成n-step的形式，将每步求和取平均然后分别计算，并且赋予系数（系数加和为1）。

$G_t^{\lambda }=(1-\lambda ){\sum }_{n=1}^{\infty }{\lambda }^{n-1}{G}_t^{(n)}$
其中$G_t^{(n)}=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+......{\gamma }^{n-1}{R}_{t+n}+{\gamma }^{n}V(S_{t+n})$

$TD\left(\lambda \right)$更新过程为：

1. 首先计算当前状态的TD偏差：${\delta }_t=R_{t+1}+\gamma V\left(S_{t+1}\right)-V\left(S_t\right)$

2)更新适合度轨迹 $E_t\left(s\right)=\{\begin{array}{l}\gamma \lambda E_{t-1},ifs̸=s_t\\ \gamma \lambda E_{t-1}+1,ifs=s_t\end{array}$

3)对于状态空间中的每个状态 s, 更新值函数：$V\left(s\right)\leftarrow V\left(s\right)+\alpha {\delta }_t{E}_t\left(s\right)$
其中$E_t\left(s\right)$称为适合度轨迹
首先，当$\lambda =0$ 时，只有当前状态值更新，此时等价于之前说的TD方法。所以TD方法又称为TD(0)方法.

其次，当$\lambda =1$时，状态s值函数总的更新与蒙特卡罗方法相同：$\begin{array}{l}{\delta }_t+\gamma {\delta }_{t+1}+{\gamma }^2{\delta }_{t+2}+\cdots +{\gamma }^{T-1-t}{\delta }_{T-1}\\ =R_{t+1}+\gamma V\left(S_{t+1}\right)-V\left(S_t\right)\\ +\gamma R_{t+2}+{\gamma }^{2}V\left(S_{t+2}\right)-\gamma V\left(S_{t+1}\right)\\ +{\gamma }^2{R}_{t+3}+{\gamma }^{3}V\left(S_{t+3}\right)-{\gamma }^{2}V\left(S_{t+2}\right)\\ ⋮\\ +{\gamma }^{T-1-t}{R}_T+{\gamma }^{T-t}V\left(S_T\right)-{\gamma }^{T-1-t}V\left(S_{T-1}\right)\end{array}$
对于一般的\lambda，前向观点等于后向观点：$\begin{array}{l}{G}_t^{\lambda }-V\left(S_t\right)=\\ -V\left(S_t\right)+\left(1-\lambda \right){\lambda }^0\left(R_{t+1}+\gamma V\left(S_{t+1}\right)\right)\\ +\left(1-\lambda \right){\lambda }^1\left(R_{t+1}+\gamma R_{t+2}+{\gamma }^{2}V\left(S_{t+2}\right)\right)\\ +\left(1-\lambda \right){\lambda }^2\left(R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+{\gamma }^{3}V\left(S_{t+2}\right)\right)+\cdots \end{array}$
$\begin{array}{l}=-V\left(S_t\right)+{\left(\gamma \lambda \right)}^0\left(R_{t+1}+\gamma V\left(S_{t+1}\right)-\gamma \lambda V\left(S_{t+1}\right)\right)\\ +{\left(\gamma \lambda \right)}^1\left(R_{t+2}+\gamma V\left(S_{t+2}\right)-\gamma \lambda V\left(S_{t+2}\right)\right)\\ +{\left(\gamma \lambda \right)}^2\left(R_{t+3}+\gamma V\left(S_{t+3}\right)-\gamma \lambda V\left(S_{t+3}\right)\right)+\cdots \end{array}\begin{array}{l}={\left(\gamma \lambda \right)}^0\left(R_{t+1}+\gamma V\left(S_{t+1}\right)-V\left(S_t\right)\right)\\ +{\left(\gamma \lambda \right)}^1\left(R_{t+2}+\gamma V\left(S_{t+2}\right)-V\left(S_{t+1}\right)\right)\\ +{\left(\gamma \lambda \right)}^2\left(R_{t+3}+\gamma V\left(S_{t+3}\right)-V\left(S_{t+2}\right)\right)+\cdots \end{array}$
$={\delta }_t+\gamma \lambda {\delta }_{t+1}+{\left(\gamma \lambda \right)}^2{\delta }_{t+2}+\cdots$

注意，所谓等价是指更新总量相等。
是不是觉得有点像Sarsa与Sarse（$\lambda$），它其实就是来自于这个原始思想

3、算法对比

对比MC算法与TD算法的特点
**MC：**无偏估计；容易收敛；可以使用函数拟合；初值不敏感；理解简单容易使用
**TD：**估计值有误差；通常情况笔MC更有效；TD（0）收敛于$V_{\pi }(s)$；初值敏感
接下来引用Sliver的PPT中的图来帮助区分这三种算法