2022年第十三届蓝桥杯省赛C/C++B组个人题解
试题 A: 九进制转十进制(数学)
算法标签 进制转换
代码
#include
#define int long long//直接把int定义成long long类型,此时主函数要变成signed main(),因为平常没有这个定义的时候,signed int =signed =int ,所以int main()=signed mian()=signed int main(),但是由于有了这个定义,int不再是int而是long long
#define endl '\n' //对于有输出缓冲的流(例如cout、clog),如果不手动进行缓冲区刷新操作,将在缓冲区满后自动刷新输出。不过对于cout来说(相对于文件输出流等),缓冲一般体现得并不明显。但是必要情况下使用endl代替'\n'一般是个好习惯
using namespace std;
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cout << 2 * pow(9, 0) + 2 * pow(9, 1) + 0 * pow(9, 2) + 2 * pow(9, 3) << endl;
return 0;
}
答案 :1478
试题 B: 顺子日期
算法标签 枚举
代码
#include
#include
#include
using namespace std;
const int months[] = {
0, 31, 28, 31, 30, 31,
30, 31, 31, 30, 31, 30,
31
};
bool check(string str)
{
for (int i = 0; i + 2 < str.size(); i ++ )
if (str[i + 1] == str[i] + 1 && str[i + 2] == str[i] + 2)
return true;
return false;
}
int main()
{
int year = 2022, month = 1, day = 1;
int res = 0;
for (int i = 0; i < 365; i ++ )
{
char str[10];
sprintf(str, "%04d%02d%02d", year, month, day);
if (check(str))
{
res ++ ;
cout << str << endl;
}
if ( ++ day > months[month])
{
day = 1;
month ++ ;
}
}
cout << res << endl;
return 0;
}
答案: 14
试题 C: 刷题统计
算法标签 模拟
代码
#include
#include
#include
using namespace std;
typedef long long LL;
int main()
{
LL a, b, n;
cin >> a >> b >> n;
LL s = 5 * a + 2 * b;
LL res = n / s * 7;
n %= s;
LL d[] = {a, a, a, a, a, b, b};
for (int i = 0; n > 0; i ++ )
{
n -= d[i];
res ++ ;
}
cout << res << endl;
return 0;
}
试题 D: 修剪灌木
算法标签
模拟 枚举
代码
#include
#include
#include
using namespace std;
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; i ++ )
cout << max(i - 1, n - i) * 2 << endl;
return 0;
}
试题 E: X 进制减法
算法标签
贪心 数学公式
思路
代码
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 100010, MOD = 1000000007;
int n, m1, m2, m;
int a[N], b[N];
int main()
{
scanf("%d", &n);
scanf("%d", &m1);
for (int i = m1 - 1; i >= 0; i -- ) scanf("%d", &a[i]);
scanf("%d", &m2);
for (int i = m2 - 1; i >= 0; i -- ) scanf("%d", &b[i]);
int m = max(m1, m2);
int res = 0;
for (int i = m - 1; i >= 0; i -- )
res = (res * (LL)max({2, a[i] + 1, b[i] + 1}) + a[i] - b[i]) % MOD;
printf("%d\n", res);
return 0;
}
试题 F: 统计子矩阵
算法标签
二维前缀和 二分
时间复杂度 O(n^3logn)
#include
using namespace std;
long long a[505][505], sum[505][505];
long long n, m, kk;
bool check(int i, int j, int k, int mid){
int now = sum[k][mid] - sum[i-1][mid] - sum[k][j-1] + sum[i-1][j-1];
if(now <= kk)
return true;
else
return false;
}
int main(){
cin >> n >> m >> kk;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
cin >> a[i][j];
}
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + a[i][j];
}
}
int res = 0;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
for(int k = i; k <= n; k++){
int l = j, r = m, ans=j-1;
while(l <= r){
int mid = (l + r) >> 1;
if(check(i,j,k,mid)){
l = mid + 1;
ans = mid;
}else{
r = mid - 1;
}
}
res += ans - j + 1; // ans 前面的都满足条件
}
}
}
cout << res << endl;
return 0;
}
算法标签
一维前缀和 双指针
时间复杂度 O(n^3)
思路
二维前缀和 → \rightarrow →一维前缀和
枚举上下边界 对每一列求一维前缀和
由于a[i]>=0 → \rightarrow →求和具有单调性 → \rightarrow →双指针
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 510;
int n, m, K;
int s[N][N];
int main()
{
scanf("%d%d%d", &n, &m, &K);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
{
scanf("%d", &s[i][j]);
s[i][j] += s[i - 1][j];
// 每一列前缀和
}
LL res = 0;
for (int i = 1; i <= n; i ++ )
for (int j = i; j <= n; j ++ )
// 枚举上下边界
for (int l = 1, r = 1, sum = 0; r <= m; r ++ )
{
// 由于具有单调性,左右边界用双指针
sum += s[j][r] - s[i - 1][r];
while (sum > K)
{
sum -= s[j][l] - s[i - 1][l];
l ++ ;
}
res += r - l + 1;
// r - l + 1 满足要求的区间长度
}
printf("%lld\n", res);
return 0;
}
试题 G: 积木画
算法标签
状态压缩DP
思路
由于面积大小为2x N, 故每个状态只有两个格子, 对于每个格子仅有拼/不拼两种状态, 故只有2^2=4种状态
f[i][j]表示已经操作完前i-1列 且第i列的状态为j的所有方案的集合
对于本题 若积木占据同时占据i,i+1两列, 我们规定为第i列操作
状态转移 由第i列4种状态转移至第i+1列4种状态 故状态转移矩阵未4*4
我们规定 若格子被占据为0 未被占据为1 且第一列方格为个位, 第一列方格为十位
可得状态转移(合法要求 在状态转移过程中,第i列必须全部占据)
int g[4][4] = {
{1, 1, 1, 1},
//初始状态 第i列未被占据 状态转移 I型积木竖置第i列 转移后状态 第i列全部占据,第i+1列为空 即g[0][0]置1
//初始状态 第i列未被占据 状态转移 L型积木第i列, 第i+1列第一行 转移后状态 第i列全部占据,第i+1列第一行占满,第二行为空即g[0][1]置1
//初始状态 第i列未被占据 状态转移 L型积木第i列, 第i+1列第二行 转移后状态 第i列全部占据,第i+1列第一行为空,第二行为占满g[0][2]置1
//初始状态 第i列未被占据 状态转移 两个I型积木横置第i列 转移后状态 第i列全部占据,第i+1列全部占据 即g[0][3]置1
{0, 0, 1, 1}, //第i列第一行被占据
{0, 1, 0, 1}, //第i列第二行被占据
{1, 0, 0, 0}, //第i列被占据
};
f[1][0] = 1;
// 最初状态
#include
#include
#include
using namespace std;
const int N = 1e7 + 10, MOD = 1e9 + 7;
int n;
int g[4][4] = {
{1, 1, 1, 1},
{0, 0, 1, 1},
{0, 1, 0, 1},
{1, 0, 0, 0},
};
int f[N][4];
int main()
{
scanf("%d", &n);
f[1][0] = 1;
for (int i = 1; i <= n; i ++ )
for (int j = 0; j < 4; j ++ )
for (int k = 0; k < 4; k ++ )
f[i + 1][k] = (f[i + 1][k] + f[i][j] * g[j][k]) % MOD;
// 能否可以从第j个状态更新为第k个状态
printf("%d\n", f[n + 1][0]);
return 0;
}
滚动数组优化
思想 用新的数据不断覆盖旧的数据量来减少空间的使用
原因 本题在更新f[i + 1][k]过程中,仅需记录f[i][j]即可 即 f[N][4]可优化为f[2][4]
#include
#include
#include
using namespace std;
const int N = 1e7 + 10, MOD = 1e9 + 7;
int n;
int g[4][4] = {
{1, 1, 1, 1},
{0, 0, 1, 1},
{0, 1, 0, 1},
{1, 0, 0, 0},
};
int f[2][4];
int main()
{
scanf("%d", &n);
f[1][0] = 1;
for (int i = 1; i <= n; i ++ )
{
memset(f[i + 1 & 1], 0, sizeof f[0]);
// 覆盖旧数据
for (int j = 0; j < 4; j ++ )
for (int k = 0; k < 4; k ++ )
f[i + 1 & 1][k] = (f[i + 1 & 1][k] + f[i & 1][j] * g[j][k]) % MOD;
// 记录新数据
}
printf("%d\n", f[n + 1 & 1][0]);
return 0;
}
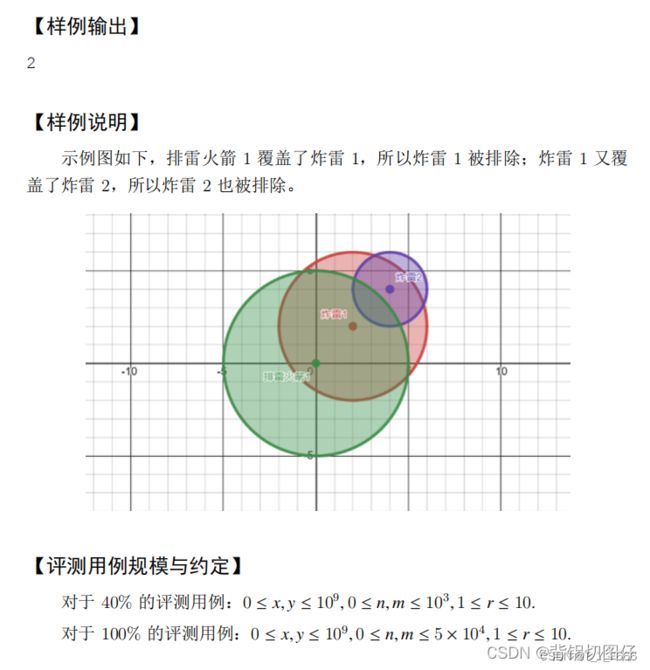
试题 H: 扫雷
算法标签
图的遍历 BFS DFS 哈希表
结论 哈希表长度 > k * 存储数据长度 k>=2 k值越大哈希表查找效率越高
#include
#include
#include
using namespace std;
typedef long long LL;
// M 哈希表长度
const int N = 50010, M = 999997;
int n, m;
struct Circle
{
int x, y, r;
}cir[N];
// 哈希表
LL h[M];
int id[M];
// 每一个点是否已经被访问
bool st[M];
// 哈希函数 x,y转换为long long类型数据
LL get_key(int x, int y)
{
// int类型数据末尾ll 数据类型转换 int-->long long
return x * 1000000001ll + y;
}
// 将long long 类型数据转化为1000000以内 便于查找
int find(int x, int y)
{
LL key = get_key(x, y);
int t = (key % M + M) % M;
while (h[t] != -1 && h[t] != key)
if ( ++ t == M)
t = 0;
return t;
}
int sqr(int x)
{
return x * x;
}
// 图的深度优先遍历
void dfs(int x, int y, int r)
{
// 标记当前点已被搜索
st[find(x, y)] = true;
//枚举雷半径内所有点
for (int i = x - r; i <= x + r; i ++ )
for (int j = y - r; j <= y + r; j ++ )
// 判断该点是否在圆内
if (sqr(i - x) + sqr(j - y) <= sqr(r))
{
// 当前点哈希值
int t = find(i, j);
// 当前点存在并且尚未访问
if (id[t] && !st[t])
// 搜索该点
dfs(i, j, cir[id[t]].r);
}
}
int main()
{
scanf("%d%d", &n, &m);
//哈希表初始化-1 表示未被使用
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i ++ )
{
int x, y, r;
scanf("%d%d%d", &x, &y, &r);
cir[i] = {x, y, r};
//x, y对应哈希值
int t = find(x, y);
if (h[t] == -1) h[t] = get_key(x, y);
// 1:该点未被存储 2:已存储半径小于当前点
if (!id[t] || cir[id[t]].r < r)
// 数据存储
id[t] = i;
}
while (m -- )
{
int x, y, r;
scanf("%d%d%d", &x, &y, &r);
// 由于圆内点不方便枚举 可枚举矩形内点
for (int i = x - r; i <= x + r; i ++ )
for (int j = y - r; j <= y + r; j ++ )
// 判断该点是否在圆内
if (sqr(i - x) + sqr(j - y) <= sqr(r))
{
// 当前点哈希值
int t = find(i, j);
// 当前点存在并且尚未访问
if (id[t] && !st[t])
// 搜索该点
dfs(i, j, cir[id[t]].r);
}
}
int res = 0;
// 枚举判断
for (int i = 1; i <= n; i ++ )
if (st[find(cir[i].x, cir[i].y)])
res ++ ;
printf("%d\n", res);
return 0;
}
试题 I: 李白打酒加强版
算法标签
DP
思路
状态表示
f[i][j][k]表示已遇到i家店,j朵花,此时壶里有k斗酒的数量
状态计算
若最后一步遇到为店 状态转移
f[i-1][j][k/2] → \rightarrow →f[i][j][k]
合法要求 i-1>0且k/2为整数
若最后一步遇到为花
f[i][j-1][k+1] → \rightarrow →f[i][j][k]
合法要求 j-1>0
#include
#include
#include
using namespace std;
const int N = 110, MOD = 1e9 + 7;
int n, m;
int f[N][N][N];
int main()
{
cin >> n >> m;
f[0][0][2] = 1;
for (int i = 0; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
for (int k = 0; k <= m; k ++ )
{
int& v = f[i][j][k];
if (i && k % 2 == 0) v = (v + f[i - 1][j][k / 2]) % MOD;
if (j) v = (v + f[i][j - 1][k + 1]) % MOD;
}
cout << f[n][m - 1][1] << endl;
return 0;
}
算法标签
贪心 堆
思路
若每一个数字都需操作,枚举出需要操作次数,除去同一层相邻相同数对对数,即为所求
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 200010, M = 10;
// 最大层数
int n, m;
// 每一层中每个数
LL f[N][M];
int main()
{
scanf("%d", &n);
// 从下向上存,需要建栈实现反转
LL stk[M];
int res = 0;
for (int i = 0; i < n; i ++ )
{
LL x;
// 栈顶下标
int top = 0;
scanf("%lld", &x);
// 入栈
while (x > 1) stk[ ++ top] = x, x = sqrt(x / 2 + 1);
// top 每一个数需要操作次数
res += top;
m = max(m, top);
// 逆序存储操作步数
for (int j = 0, k = top; k; j ++, k -- )
f[i][j] = stk[k];
}
//枚举所有层数
for (int i = 0; i < m; i ++ )
// 同一层相邻相同数对对数
for (int j = 1; j < n; j ++ )
if (f[j][i] && f[j][i] == f[j - 1][i])
res -- ;
printf("%d\n", res);
return 0;
}
优先队列解法,时间复杂度 O(6nlogn)
思路
利用优先队列记录连续的一段相同高度(v:记录高度)的竹子, 由于涉及区间合并,故需要记录左端点(l:记录左端点)
#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 200010;
int n;
LL h[N];
struct Seg
{
int l, r;
LL v;
bool operator< (const Seg& S) const
{
if (v != S.v) return v < S.v;
return l > S.l;
}
};
LL f(LL x)
{
return sqrt(x / 2 + 1);
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%lld", &h[i]);
priority_queue heap;
for (int i = 0; i < n; i ++ )
{
int j = i + 1;
while (j < n && h[i] == h[j]) j ++ ;
heap.push({i, j - 1, h[i]});
i = j - 1;
}
int res = 0;
// 1:连续一段 2:长度大于一
while (heap.size() > 1 || heap.top().v > 1)
{
auto t = heap.top();
heap.pop();
//区间合并 1:长度相等 2:连续
while (heap.size() && heap.top().v == t.v && t.r + 1 == heap.top().l)
{
// 更新原区间右端点
t.r = heap.top().r;
// 对于被合并区间 弹出队列
heap.pop();
}
// 新区间入队
heap.push({t.l, t.r, f(t.v)});
// 对合并后区间使用魔法
if (t.v > 1) res ++ ;
}
printf("%d\n", res);
return 0;
}
除A题及F题第一种解法 其余代码为Acwing y总代码
y总B站讲解地址
图片转自CSDN @背锅切图的
原创不易 转载请标明出处
如果对你有所帮助 别忘啦点赞支持哈![]()