python算法模板第一部分(2)(前缀和与差分)
注:本文是在学习了acwing的算法基础课后撰写,主要用于记录python版本算法的模板。其中部分参考了acwing众多大佬的题解。
1.一维前缀和
思想:
原数组 a 1 a 2 . . . a n a_1 a_2...a_n a1a2...an
前缀和 S i = a 1 + a 2 + . . . + a i S_i = a_1 + a_2 + ... + a_i Si=a1+a2+...+ai (下标从1开始方便计算),定义 S 0 = 0 S_0 = 0 S0=0
前缀和的作用:快速求出原数组中一段数的和。
例如,求 [l, r] 区间内数组a的和,不需要遍历a [l, r]部分,只需要 S r − S l − 1 S_r - S_{l-1} Sr−Sl−1即可。也就是说计算的时间从O(n)降为了O(1),但计算前缀和数组需要O(n)的时间。因此只求一段数的和实际上没必要使用计算前缀和,但当我们要计算多段时,前缀和就可以节省时间。
步骤:
1.求前缀和 S i = a 1 + a 2 + . . . + a i S_i = a_1 + a_2 + ... + a_i Si=a1+a2+...+ai
2.对前缀和做减法,求部分和 a l + . . . + a r = S r − S l − 1 a_l + ... + a_r = S_r - S_{l-1} al+...+ar=Sr−Sl−1
模板:
if __name__ == "__main__":
n, m = map(int, input().split())
nums = list(map(int, input().split()))
prefix = [0] * (n + 10) # 前缀和数组
for i in range(n):
prefix[i+1] = prefix[i] + nums[i] # 求前缀和
for i in range(m):
l, r = map(int, input().split())
print(prefix[r] - prefix[l-1]) # 求部分和
2.二维前缀和
思想:
已知矩阵,快速求子矩阵和。思想基本与一维一致。
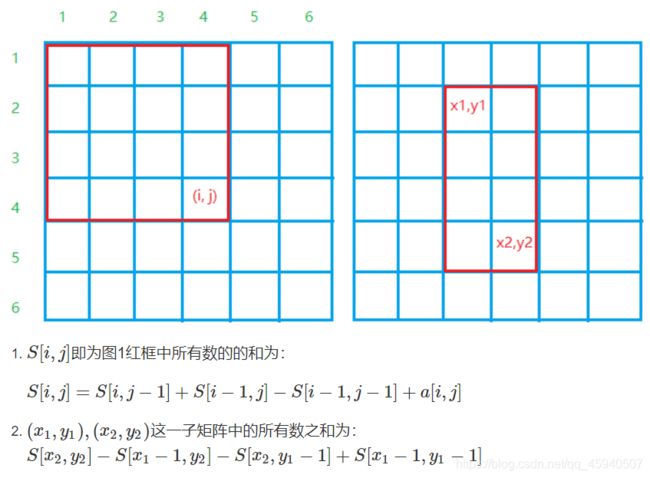
上图源于acwing796题题解
不记得公式时,可以绘制类似上图的表格推公式。
步骤:
1.求前缀和 S i j = S ( i − 1 ) j − S i ( j − 1 ) − S ( i − 1 ) ( j − 1 ) + a i j S_{ij} = S_{(i-1)j} - S_{i(j-1)} - S_{(i-1)(j-1)} + a_{ij} Sij=S(i−1)j−Si(j−1)−S(i−1)(j−1)+aij
2.求部分和 = S x 2 y 2 − S x 2 ( y 1 − 1 ) − S ( x 1 − 1 ) y 2 + S ( x 1 − 1 ) ( y 1 − 1 ) =S_{x_2y_2} - S_{x_2(y_1-1)} - S_{(x_1-1)y_2} + S_{(x_1-1)(y_1-1)} =Sx2y2−Sx2(y1−1)−S(x1−1)y2+S(x1−1)(y1−1)
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和
模板:
if __name__ == "__main__":
n, m, q = map(int, input().split())
nums = []
for _ in range(n):
nums.append([int(i) for i in input().split()])
# 1.计算前缀和
s = [[0]*(m+1) for _ in range(n+1)]
for i in range(1, n+1):
for j in range(1, m+1):
s[i][j] = nums[i-1][j-1] + s[i-1][j] + s[i][j-1] - s[i-1][j-1]
ans = []
# 2.计算区域和
for _ in range(q):
x1, y1, x2, y2 = map(int, input().split())
ans.append(s[x2][y2] - s[x2][y1-1] - s[x1-1][y2] + s[x1-1][y1-1])
print('\n'.join(map(str, ans)))
3.一阶差分
思想:
差分是前缀和的逆运算。是已知前缀和数组推原数组的过程。
即已知 a 1 a 2 . . . a i a_1a_2...a_i a1a2...ai,构造 b 1 b 2 . . . b i b_1b_2...b_i b1b2...bi,使得 a i = b 1 + b 2 + . . . + b i a_i = b_1 + b_2 + ... + b_i ai=b1+b2+...+bi。
差分的作用:若要修改 a l . . . a r a_l...a_r al...ar内的元素+c,只需将 b l b_l bl+c, b r + 1 b_{r+1} br+1-c。将这步操作称为insert,insert函数就是差分的核心。
构建初始差分数组也可以通过insert完成。具体可见代码。
步骤:
1.构建初始差分数组b(遍历数组a,对数组b在i位置插a[i])
2.根据题意修改差分数组
3.利用修改后的差分数组重新计算前缀和
模板:
# 核心
def insert(b, l, r, c):
b[l] += c
b[r+1] -= c
if __name__ == "__main__":
n, m = map(int, input().split())
a = [0] * (n + 10) # 原数组
b = [0] * (n + 10) # 差分数组
nums = list(map(int, input().split()))
for index, val in enumerate(nums):
a[index+1] = val
# 构建初始差分数组b[]
for i in range(1, n+1):
insert(b, i, i, a[i])
# 根据题意修改差分数组
while m > 0:
m -= 1
l, r, c = map(int, input().split())
insert(b, l, r, c)
# 利用修改后的差分数组重新计算前缀和
for i in range(1, n+1):
b[i] += b[i-1]
for i in range(1, n+1):
print(b[i], end=" ")
4.二阶差分
思想:
与一维基本一致,重点关注insert部分的不同。
若要对原数组a修改以(x1, y1)为左上角,(x2, y2)为右下角的矩阵块。需要对差分数组b做如下步骤:
b[x1][y1] += c
b[x2+1][y1] -= c
b[x1][y2+1] -= c
b[x2+1][y2+1] += c
步骤:
与一维一致。
1.构建初始差分数组b
2.根据题意修改差分数组
3.利用修改后的差分数组重新计算前缀和
模板:
# 核心
def insert(b, x1, y1, x2, y2, c):
b[x1][y1] += c
b[x2+1][y1] -= c
b[x1][y2+1] -= c
b[x2+1][y2+1] += c
if __name__ == "__main__":
m, n, q = map(int, input().split())
a = [[0 for _ in range(n+10)] for _ in range(m+10)]
b = [[0 for _ in range(n+10)] for _ in range(m+10)]
for i in range(1, m+1):
nums = list(map(int, input().split()))
for j, val in enumerate(nums):
a[i][j+1] = val
# 构建初始差分数组b[][]
for i in range(1, m+1):
for j in range(1, n+1):
insert(b, i, j, i, j, a[i][j])
# 根据题意修改差分数组
while q > 0:
q -= 1
x1, y1, x2, y2, c = map(int, input().split())
insert(b, x1, y1, x2, y2, c)
# 利用修改后的差分数组重新计算前缀和
for i in range(1, m+1):
for j in range(1, n+1):
a[i][j] = a[i-1][j] + a[i][j-1] - a[i-1][j-1] + b[i][j]
for i in range(1, m+1):
for j in range(1, n+1):
print(a[i][j], end=" ")
print()