【动态规划模板】神似的01和完全背包、多重背包和分组背包问题

神似的01背包与完全背包

 【经典题目】01背包采药

题目描述

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说: "孩子，这个山洞里有一些不同的草药， 采每一株都需要一 些时间， 每一株也有它自身的价值。 我会给你- -段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。如果你是辰辰，你能完成这个任务吗?

输入格式

第一行有2个整数T (1≤T≤1000)和M (1≤M≤100)，用一个空格隔开，T代表总共能够

用来采药的时间，M代表山洞里的草药的数目。

接下来的M行每行包括两个在1到100之间(包括1和100)的整数,分别表示采摘某株草药的时间和这株草药的价值。

输出格式

输出在规定时间内可以采到的药草的最大总价值。

输入样例：

70 3
71 100
69 1
1 2

输出样例： 

3 

 数据范围

• 对于30%的数据，;
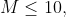• 对于全部数据， 。

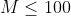AC Code（01背包）

'''
# #AC Code（01背包)# #
'''
V, N = map(int, input().split())
 
dp = [0] * (V + 1)
for i in range(N):
    v, w = map(int, input().split()) # 体积和价值(权重)
    for j in range(V, v-1, -1):
        dp[j] = max(dp[j], dp[j-v] + w)
    
print(dp[V])

AC Code （完全背包）

'''
# #AC Code（完全背包)# #
NOTE：完全背包和01背包不同点：每种草药可以无限制的疯狂采摘。
'''
V, N = map(int, input().split())
 
dp = [0] * (V + 1)
for i in range(N):
    v, w = map(int, input().split()) # 体积和价值(权重)
    for j in range(v, V+1):
        dp[j] = max(dp[j], dp[j-v] + w)
    
print(dp[V])

 多重背包问题

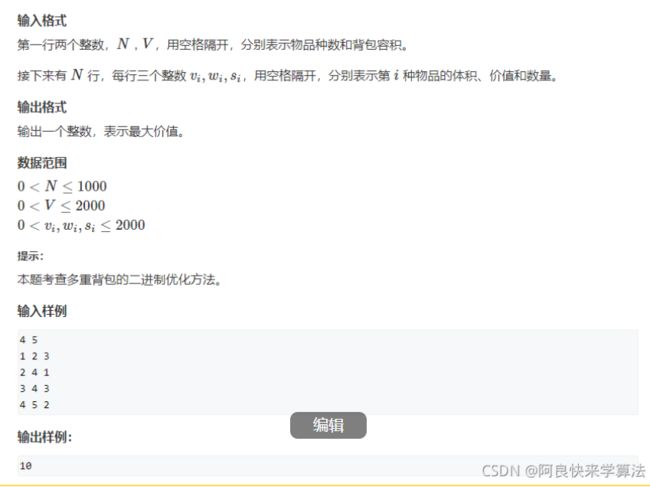
有N种物品和一个容量是V的背包。

第i种物品最多有s件，每件体积是v，价值是i。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。输出最大价值。

 AC Code 

'''
# #AC Code（多重背包)# #
'''
if __name__ == "__main__":
    N, V = map(int, input().split())
    dp = [0] * (V + 1)
    v = []
    w = []
    for _ in range(N):
        a, b, c = map(int, input().split())
        k = 1
        while c > k:
            v.append(a*k)
            w.append(b*k)
            c -= k
            k *= 2
        if c:
            v.append(a*c)
            w.append(b*c)
    for i in range(len(v)):
        for j in range(V, v[i]-1, -1):
            dp[j] = max(dp[j], dp[j - v[i]] + w[i])

    print(dp[V])

分组背包问题

有 N 组物品和一个容量是 V 的背包。

每组物品有若干个，同一组内的物品最多只能选一个。

每件物品的体积是v(i,j)，价值是w(i,j)，其中 i 是组号，j 是组内编号。

求解哪些物品装入背包，可使得物品总体积不超过背包容量，且总价值最大。

输出最大价值。

AC Code

'''
# #AC Code（分组背包)# #
'''
if __name__ == "__main__":
    N, V = map(int, input().split())
    v = []
    w = []
    s = []
    dp = [0] * (V + 1)
    for i in range(N):
        s.append(int(input()))
        tv = []
        tw = []
        for j in range(s[i]):
            a, b = map(int, input().split())
            tv.append(a)
            tw.append(b)
        v.append(tv)
        w.append(tw)
        
    for i in range(N):
        for j in range(V, 0- 1, -1):
            for k in range(s[i]):
                if j >= v[i][k]:
                    dp[j] = max(dp[j],dp[j-v[i][k]]+w[i][k])
    print(dp[V])