平衡二叉树 AVL树 实现 C语言
定义: 为避免树的高度增长过快,降低二叉排序树的性能,规定在插入和删除二叉树结点时,要保证任意结点的左右子树的高度差的绝对值不超过1.将这样的二叉树称为平衡二叉树,简称平衡树。
平衡因子: 结点左子树和右子树的高度差,平衡树平衡因子取值只可能是-1、0、1。
1、LL平衡旋转(右单旋转)
在结点A的左孩子(L)的左子树(L)上插入新节点。
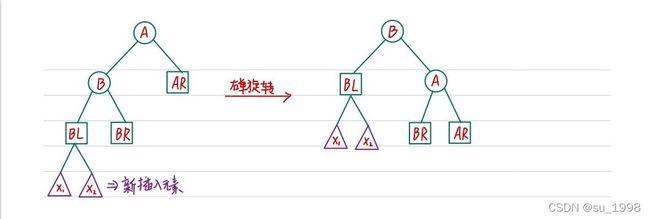
/* LL单旋 */
static Position SingleRotateWithRight(Position A)
{
Position B;
B = A->Left;
A->Left= B->Right;
B->Left = A;
A->Height = Max(Height(A->Left), Height(A->Right)) + 1;
B->Height = Max(Height(B->Left),A->Height) + 1;
return B; /*New root */
}
2、RR平衡旋转(左单旋转)
在结点A的右孩子(R)的右子树(R)上插入新节点。

/* 向左单旋 */
static Position SingleRotateWithLeft(Position A)
{
Position B;
B= A->Right;
A->Right= B->Left;
B->Left= A;
A->Height = Max(Height(A->Left), Height(A->Right)) + 1;
B->Height = Max(A->Height,Height(B->Right)) + 1;
return B; /* New Root */
}
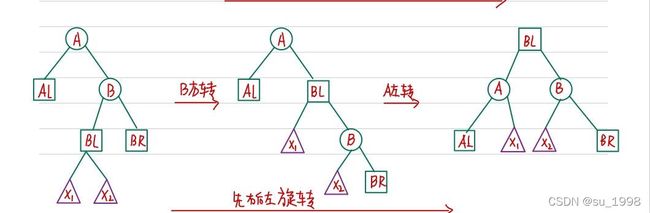
3、LR平衡旋转(先左后右双旋转)
在结点A的左孩子(L)的右子树(R)上插入新节点。

/* 先左后右双旋 */
static Position DoubleRotateWithLeft(Position A)
{
/* Rotate between K1 and K2 */
A->Left = SingleRotateWithRight(A->Left);
/* Rotate between K3 and K2 */
return SingleRotateWithLeft(A);
}
2、RL平衡旋转(先右后左双旋转)
在结点A的右孩子(R)的左子树(L)上插入新节点。
/* 先右后左双旋 */
static Position DoubleRotateWithRight(Position A)
{
A->Right = SingleRotateWithLeft(A->Right);
return SingleRotateWithRight(A);
}
代码实现:
#include
//对Avl树进行插入操作,非递归版本
Avltree Insert_not_recursion (int x, Avltree T)
{
stack<Avltree> route; //定义一个堆栈使用
//找到元素x应该大概插入的位置,但是还没进行插入
Avltree root = T;
while(1)
{
if(T == NULL) //如果T为空树,就创建一棵树,并返回
{
T = static_cast<Avltree>(malloc(sizeof(struct AvlNode)));
if (T == NULL) cout << "out of space!!!" << endl;
else
{
T->Element = x;
T->Left = NULL;
T->Right = NULL;
T->Hight = 0;
T->Isdelete = 0;
route.push (T);
break;
}
}
else if (x < T->Element)
{
route.push (T);
T = T->Left;
continue;
}
else if (x > T->Element)
{
route.push (T);
T = T->Right;
continue;
}
else
{
T->Isdelete = 0;
return root;
}
}
//接下来进行插入和旋转操作
Avltree father,son;
while(1)
{
son = route.top ();
route.pop(); //弹出一个元素
if(route.empty())
return son;
father = route.top ();
route.pop(); //弹出一个元素
if(father->Element < son->Element ) //儿子在右边
{
father->Right = son;
if( Height(father->Right) - Height(father->Left) == 2)
{
if(x > Element(father->Right))
father = SingleRotateWithRight(father);
else
father = DoubleRotateWithRight(father);
}
route.push(father);
}
else if (father->Element > son->Element) //儿子在左边
{
father->Left = son;
if(Height(father->Left) - Height(father->Right) == 2)
{
if(x < Element(father->Left))
father = SingleRotateWithLeft(father);
else
father = DoubleRotateWithLeft(father);
}
route.push(father);
}
father->Hight = max(Height(father->Left),Height(father->Right )) + 1;
}
}

