贪心算法-背包、有期限作业排序、单源最短路径、二元归并
贪心算法的实验—学习过程
文章目录
- 前言
- 一、(部分)(分数)背包问题(调制饮品问题)
- 二、 用贪心法实现带有期限作业排序的快速算法
- 三、用贪心算法实现单源最短路径问题(Dijkstra)
- 四、实现K元归并树贪心算法(做2元归并树)
- 五、结果合集
- 六、总结
- 七、可复制的代码
-
- 1.背包
- 2.有期限作业排序
- 3.单源最短路径
- 4.二元归并树
注:这是本人写的第四次实验,由于很懒,只是把报告内容搬运了过来,如有不足,请理解。没有认真设置文章格式,而且也没为文章做专门的修改请理解。
前言
实验前言:本次实验学习贪心策略,为此其实我们可以学到很多,大部分文档都在着重讲解贪心为什么正确,它是如何做的。但是还要知道:“完美是优秀的敌人”有时候只需要找到一个能大致解决问题的方法,贪心策略很多时候显然不能够获得最优解,但是可以获得一个非常接近最优解的解。尤其在考虑复杂的NP完全问题时,近似也是不错的方法。(学习感悟:步步完美,虽然可能不是最优解,但是也近似最优解。有时候不追求完美退而求其次反而能得到完美的结果。人生就像连绵不断的曲线,起起落落是人生常态……这说的不就是贪心算法!)
数学:在学习本次实验的过程中,我联想到了很多数学知识,从数学的证明到数学中的多元函数极值问题再到离散数学中的集合知识,我认为这部分的学习是很需要逻辑的,如果用数学的严谨、数学的方法、来考虑可能会很简单。
顺序:本次实验从背包问题入手,由简单到复杂,逐渐深入。在数据结构方面,我考虑了向量结构、struct结构、优先队列结构(priority_queue)。
一、(部分)(分数)背包问题(调制饮品问题)
问题:本问题的描述完全相似于01背包,增加的条件是可以装一部分物品进入背包。贪心策略的思想符合人的本性,且易于理解。找零钱、拿物品等等人自然想到的就是贪心策略,在该问题中很自然的考虑性价比,先选性价比高的物品,依次装入直到装满。但是为什么这个贪心策略可以在该问题中得到最优解,如何证明是关键的一步,一般使用替换法证明,当然还可以联想很多其它数学证明法,如反证法、归纳法等等。
证明:假设另外存在最优解s*,贪心解为s’,并且按照性价比排好顺序。一开始假设放入一样多的性价比最高的物品。然后往上依次看,直到某一性价比的物品,贪心解装满了,最优解没装满,那么我们可以把最优解中没装满的物品的下一个低性价比的物品换成这个高性价比的物品,这样的交换肯定不亏。这样以此类推,最优解的价钱不会减少,而且换完之后最优解会变成贪心解。(为此我画了一张图,帮助理解)
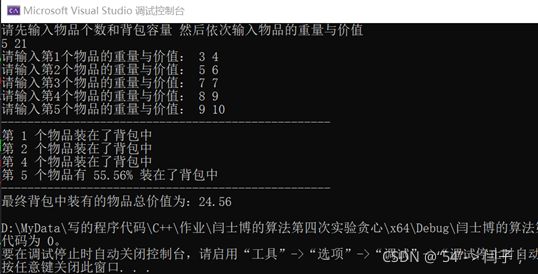
做为引入的问题,比较简单,故深入的理解在后面的问题讨论,下面是背包问题的代码:(完全自主编写,貌似写的有点复杂)


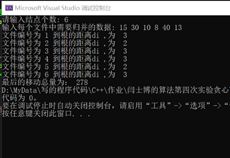
代码的运行结果:测试了一些01背包中的数据,可以验证是正确的。
二、 用贪心法实现带有期限作业排序的快速算法
我打算通过这一部分的实验,探索如何掌握并自己设计贪心算法,而不是只是弄懂个别案例。首先我通过很多资料,学习设计贪心算法的过程。
对于该问题,一个好的入手点是首先考虑动态规划,然后设计一个递归,证明我们可以通过一个贪心选择使只剩下一个子问题,再证明贪心选择的安全性,最后设计一个递归的贪心策略,再把贪心策略转换为递归策略(《算法导论》)。我阅读了很多的资料,直到看到这个繁琐的过程,我认为这是一个好的入手点,可以帮助我独自想出该问题的贪心算法的解。我们应该知道,在每个贪心算法之下,几乎总有一个更繁琐的动态规划算法。
在开始之前,还要注意贪心选择性质,该性质代表我们在当前问题不用考虑子问题的解(不依赖于任何将来的选择),而动态规划则通常依赖于子问题的解。如果我们在贪心中考虑了众多选择,则说明我们的算法还可以改进。最优子结构性质在贪心中真正要做的工作就是论证:将子问题与贪心选择组合在一起就能生成原问题的最优解。
开始(前面其实都是废话):动态规划,表格,行表示考虑的作业范围,列表示期限(找到期限最久的作业,作为列数)。每次考虑完成该作业与不完成该作业两个情况的收益,选择最大的收益填入表格,如果不选该作业,则就是上一行的值,如果选该作业,则为上一行在该作业截至日期-1列处的值。当然每次也必须考虑有没有入场券,即能不能选择该作业。可以思考“带权重的活动选择问题”。
贪心选择:结合递归考虑,我发现本问题的贪心选择为作业的收益(当然可能有其它的贪心选择,比如按照最短期限等等,但是可以举反例证明一些贪心选择并不适用)。简单证明,有个贪心解,和一个最优解,对于第一个作业,如果没有把计算机的资源分给收益最高的作业,那么我就可以把分给的资源换成贪心的分配,这样总收益不会降低。然后使用数学归纳法,每次贪心求完之后,递归的求剩下的相容的部分。总的来说,思路还是一样的。
该问题的约束:所有作业均应该在期限之前完成。该问题的目标:使收益之和最大。
按照这个思路,我的实现的核心代码:(贪心的求解):

时间复杂度:对我的代码进行分析,发现最坏情况时间复杂度为O(n^2),最好情况下为O(n),空间复杂度为存储的几个数据结构O(n)。
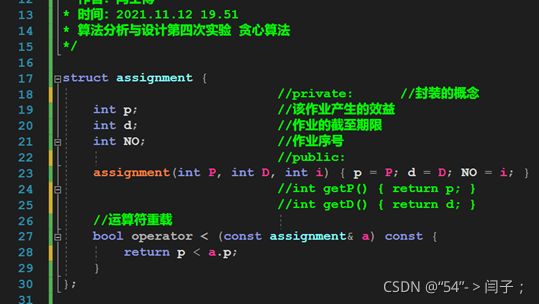
下面使我的全部代码:其中有专门实现输入的代码段,有定义任务这个结构体的代码段,有定义了一些使用到的数据结构的代码段,最核心的代码其实只有上面的一小点,其余跟前面我写的背包问题的代码类似。(在写的时候我专门注意了可读性,中间有一段很长的注释,是我刚开始的错误思路,通过验证发现错了,并又思考了一种实现,但是为了记录实验的过程只是注释了起来,并未删除)(完全是根据自己的思路写的,不知道是不是高效的方法,使用了很多STL中的数据结构,“数据结构”课程上学到的知识)
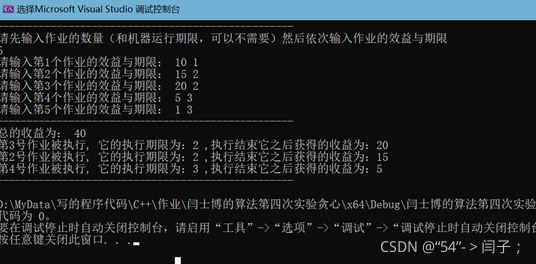

后:该问题,我们可以发现,贪心算法可以从动态规划开始,在加入一些限制条件后贪心算法也可以转换为使用动态规划的问题(比如会场安排问题增加每个活动的收益)。作业问题,如果作业的时间长短不一的限制,则贪心算法是这个NP问题的很好的近似。
对比:通过对比发现,分而治之主要解决独立子问题,动态规划主要解决重叠子问题,贪心策略主要解决单一子问题。而且贪心选择的方式也多种多样,每一种贪心选择是否能够解决问题都需要证明。(下面是我认为很好的一张图)
三、用贪心算法实现单源最短路径问题(Dijkstra)
还记得在学习计算机网络的控制平面的时候,学习路由器选择算法,学习了链路状态路由算法(link state routing)就是通过dijkstra算法找出的最短路径,然后生成汇集树(sink tree),从那时起就学习了单元最短路径问题。
由于该问题的算法已经多次学习,并且课堂上也做了重点讲解,所以在该实验中主要给出实现与证明。(实现可能使用优先级序列等数据结构会更高效一一点点,比书上的方法,这样每次弹出队列最前面的数据就可以实现,而不需要每次遍历一遍找剩余的里面的路径最小值)在理解该算法的时候,可以参考上一部分最后的图,贪心每次考察局部直至最优,这就是对Dijkstra最好的理解了吧。
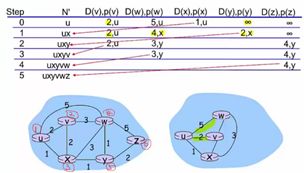
先给出代码与实例,再说证明,实例是上学期计算机网络的期末复习题,如今使用自己写的代码求出了它。
证明(简述):该证明在贪心策略处用了反证法,在最优子结构里用了数学归纳法的思想。我的理解如下:在这个算法里,把节点分为了两组“己方”即已经确定了最短路径的点,和外部点。每次从外部选一个最近可达的作为己方点。已知下一个外部最近可达的点为x点,假设从起点到x的最短距离不是从一个己方点y到x的距离,而要经过一个外部点z。那么根据这个假设,距离y z加z x小于距离y x,距离均为正数,由此可推出距离y z小于距离y x,但是已知y x最小(每次从外部选一个最近可达的作为己方点,这次选的是x,所以y x最小)所以矛盾,所以假设不成立,所以起点到x的最短距离就确定了,己方点加一。
再用归纳的方法,或者是每次把己方的点看为一个点,就可以推出最优解是这个贪心解。
时间复杂度:两层嵌套循环O(n*n)。空间复杂度,是创建的存储数据的数组所占据的空间O(n),存储短距离的数组与存储己方的数组还有一个用于追踪最优解的数组。
最后,解决该问题的方法还有Bellman-Ford算法等等,对于相关的概念还需要认真的学习,这里的贪心策略Dijkstra算法只是很简单的一部分。
四、实现K元归并树贪心算法(做2元归并树)
看完这部分的实验要求,总感觉和Huffman code很像,要构造树。树在学习数据结构中我们知道,一般要使用链表来构造,优势是删除与插入快,但是也可以使用向量,优势是随机查询快。Huffman code在数据结构、交互式多媒体等多门课程中有学习与实现,其实现方式采用了最小优先队列的方式。贪心的策略是每次合并最小的两个节点。
本部分的核心代码:
简单证明:还是反证法,如果最优解中最深的叶子需要归并的数据不是最少的,那么可以和上面的归并数据最少的叶子交换,交换之后的代价不会增加,所以最底层的叶子是归并数据最少的文件。然后递归把两个节点看成一个节点,继续贪心。
五、结果合集
六、总结
七、可复制的代码
1.背包
#include
#include
#include
#include
#include"TaskSet.h"
using namespace std;
/*
* 任务3 (部分)背包问题(调制饮品问题)
* 作者:
* 时间:2021.11.10 19.51
* 算法分析与设计第四次实验 贪心算法
*/
//定义一个结构体,商品,包含三个信息,价值重量,与性价比
struct goods {
float value;
float weight;
float costPerformance;
int NO; //编号
float portion; //最后一个物品,选择了百分之多少的部分
};
//直接采用手动设置参数,也可以使用cin的方式输入参数
void inputOrSetPar(vector& Goods, float& capacity) {
goods a;
int n;
cout << "请先输入物品个数和背包容量 然后依次输入物品的重量与价值 " << endl;
cin >> n >> capacity;
for (int i = 0; i < n; i++) {
cout << "请输入第" << i+1 << "个物品的重量与价值: ";
cin >> a.weight >> a.value;
Goods.push_back(a);
}
}
//定义一个比较大小的函数,直接调用STL的sort进行排序
bool compare(const goods& a, const goods& b) {
return !(a.costPerformance < b.costPerformance);
}
//背包问题的核心实现(使用贪心算法),使用了数据结构与STL中的vector数据结构与sort标准函数
void knapsack(vector &Goods,float& capacity) {
inputOrSetPar(Goods, capacity);
int n = Goods.size(); //物品个数
//计算性价比
for (int i = 0; i < n; i++) {
Goods[i].NO = i+1;
Goods[i].costPerformance = Goods[i].value / Goods[i].weight;
}
//排序,使用了compara函数
sort(Goods.begin(), Goods.end(),compare);
//数据结构,存解 ,最优值 ,和一个计数
vector solution(n,0);
float totalValue = 0;
int i; //因为后面还会使用i
//因为是小于没有等于,所以最后背包一定有空余空间
//!!!!!!------贪心算法最核心的代码,很好理解,每次选性价比最高的物品---------!!!!!!//
for (i = 0; Goods[i].weight < capacity; i++) {
solution[i] = 1;
capacity = capacity - Goods[i].weight;
totalValue += Goods[i].value;
}
Goods[i].portion = capacity / Goods[i].weight;
totalValue += Goods[i].portion * Goods[i].value;
solution[i] = 1;
cout << "--------------------------------------------------" << endl;
for (int j = 0; j < n; j++) {
if (solution[j] == 1 && j != i)
cout << "第 " << Goods[j].NO << " 个物品装在了背包中 " << endl;
else if (j == i) {
cout << "第 " << Goods[i].NO << " 个物品有 "
<< setprecision(4)<< Goods[i].portion * 100 << "% 装在了背包中" << endl;
break;
}
}
cout << "--------------------------------------------------" << endl;
cout << "最终背包中装有的物品总价值为:" << totalValue << endl;
}
int main() {
vector Goods;
float capacity;
knapsack(Goods, capacity);
return 0;
}
2.有期限作业排序
#include
#include
#include
#include
#include
#include
#include"TaskSet.h"
using namespace std;
/*
* 任务1 用贪心法实现带有期限作业排序的快速算法
* 作者:
* 时间:2021.11.12 19.51
* 算法分析与设计第四次实验 贪心算法
*/
struct assignment {
//private: //封装的概念
int p; //该作业产生的效益
int d; //作业的截至期限
int NO; //作业序号
//public:
assignment(int P, int D, int i) { p = P; d = D; NO = i; }
//int getP() { return p; }
//int getD() { return d; }
//运算符重载
bool operator < (const assignment& a) const {
return p < a.p;
}
};
//使用优先级队列,思路结构与背包问题类似
void inputOrSetPar(priority_queue& Assignment) {
//priority_queue , less > a;
int n;
cout << "请先输入作业的数量(和机器运行期限,可以不需要)然后依次输入作业的效益与期限 " << endl;
cin >> n ;
for (int i = 0; i < n; i++) {
int p; int d;
cout << "请输入第" << i + 1 << "个作业的效益与期限: ";
cin >> p >> d;
assignment a(p,d,i+1);
Assignment.push(a); //按效益从高到低排序
}
}
void job_sequencing(priority_queue& Assignment) {
cout << "--------------------------------------------------" << endl;
inputOrSetPar(Assignment);
cout << "--------------------------------------------------" << endl;
int total_P; //总的效益
//int Machine_life; //机器运行期限,没有这个限制
vector Jobs_performed; //存该机器执行的作业,当然也可以只存int(作业号)值
set machine_work_time; //存取机器工作的时间
//一些数据结构
Jobs_performed.push_back(Assignment.top());
machine_work_time.insert(Assignment.top().d);
total_P = Assignment.top().p;
Assignment.pop();
//!!!!!!!!!!!!!!贪心策略,核心代码!!!!!!!!!!!//
//判断能否在期限内完成
while (!Assignment.empty()){ //判断我想到了set或者再创建一个存执行任务的数组
//方案一,存一个很大的数组,初始是每个单位时间没有作业(-1)
// ,对于每个作业,如果该数组值为-1,则可执行,否则不能执行
//但是因为学过数据结构,我考虑使用STL中的集合,判断有无重复
/*
//!!错了!!!,这是最初的想法,但是这样是不对的,因为前面的时间如果有空余,机器会空闲,则可能不对
if (!machine_work_time.count(Assignment.top().d)) { //集合J并上当前作业,这些作业可以在截至日期前完成
machine_work_time.insert(Assignment.top().d);
Jobs_performed.push_back(Assignment.top());
total_P += Assignment.top().p;
Assignment.pop();
}
else
Assignment.pop();
*/
//思考了前面写法错误的原因,重新写的,从后往前查找机器有无空余时间,这次测试了很多数据,均正确了
int i;
for (i = Assignment.top().d; machine_work_time.count(i); i--);
if (i > 0) {
machine_work_time.insert(i);
Jobs_performed.push_back(Assignment.top());
total_P += Assignment.top().p;
Assignment.pop();
}
else
Assignment.pop();
}
//可以调用sort对Jobs_performed里存的作业的期限排序,确定谁先执行,可能会更好看一些,但是目前这样也是可以的。(已经求出了完成哪一些作业)
cout << "总的收益为: " << total_P << endl;
for (int i = 0; i < Jobs_performed.size(); i++) {
cout << "第" << Jobs_performed[i].NO << "号作业被执行," << " 它的执行期限为:" << Jobs_performed[i].d
<< " ,执行结束它之后获得的收益为:" << Jobs_performed[i].p << endl;
}
cout << "--------------------------------------------------" << endl;
}
int main() {
priority_queue , less > Assignment;
job_sequencing(Assignment);
}
3.单源最短路径
#include
using namespace std;
const int maxnum = 100;
const int infinity = INT_MAX;
//我习惯把无穷设置为-1,但是在判断的时候不能直接<,所以沿用了书上的方式
/*
* 作者:
* 时间:2021.11.12
* 贪心算法实验任务四
* 注:由于该算法学习了很多次,上课也有详细的讲解,故减少了注释,直接给了实现
*/
//核心代码
void Dijkstra(int n, int v, int* dist, int* prev, int **c)
{
bool *s = new bool[n];
for (int i = 1; i <= n; ++i)
{
dist[i] = c[v][i];
s[i] = 0;
if (dist[i] == infinity)
prev[i] = 0;
else
prev[i] = v;
}
dist[v] = 0;
s[v] = 1;
for (int i = 2; i <= n; ++i)
{
int tmp = infinity;
int u = v;
//-------------------------------------------------------------------------------------
//这里如果使用优先级序列可能会更好
//每次直接弹出top,然后再pop,这样可以节省很多的时间
//但是如果使用普通的C代码,不使用STL的内容,这种实现很好,课本就是这样的实现
for (int j = 1; j <= n; ++j)
if ((!s[j]) && dist[j] < tmp)
{
u = j;
tmp = dist[j];
}
s[u] = 1;
for (int k = 1; k <= n; k++)
if (dist[k] == infinity)
printf("%8s", "无穷远");
else
printf("%8d", dist[k]);
cout << endl;
//-------------------------------------------------------------------------------------
for (int j = 1; j <= n; ++j)
if ((!s[j]) && c[u][j] < infinity)
{
int newdist = dist[u] + c[u][j];
if (newdist < dist[j])
{
dist[j] = newdist;
prev[j] = u;
}
}
}
cout << "//!!!!!----------------------------------------------!!!!!// " << endl;
cout << endl;
}
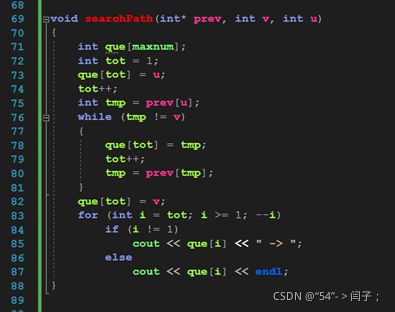
void searchPath(int* prev, int v, int u)
{
int que[maxnum];
int tot = 1;
que[tot] = u;
tot++;
int tmp = prev[u];
while (tmp != v)
{
que[tot] = tmp;
tot++;
tmp = prev[tmp];
}
que[tot] = v;
for (int i = tot; i >= 1; --i)
if (i != 1)
cout << que[i] << " -> ";
else
cout << que[i] << endl;
}
4.二元归并树
//构造哈夫曼树
//2元归并树核心代码!!!!!!
void huffmanTree(priority_queue& q) {
while (q.size() != 1) {
Node* left = new Node(q.top()); q.pop();
Node* right = new Node(q.top()); q.pop();
Node node('R', left->frequency + right->frequency, left, right);
q.push(node);
}
}