机器人轨迹规划—五次多项式插值轨迹
机器人轨迹
这一系列轨迹教程将主要包括以下内容:
-
点到点轨迹(P2P)
- 五次多项式插值轨迹
- 三次多项式插值轨迹
- 多项式轨迹实战
- 梯形速度曲线轨迹
- 双S形速度曲线轨迹
- 多个自由度轨迹的时间同步
-
在线轨迹规划
- 多项式在线轨迹规划
- 梯形在线轨迹规划
- 双S形在线轨迹规划
- 非线性实时轨迹滤波
-
多点轨迹(Multi-point)
- 三次样条曲线(cubic spline)
- 贝赛尔曲线(Bezier Curve)
- B样条曲线(BSpline)
-
时间最优轨迹
- 三次样条时间最优轨迹
- 任意路径下的时间最优轨迹
- 时间最优停止轨迹
- 不约束路径
- 有路径约束
这一篇文章讲五次多项式插值轨迹。
文章目录
-
- 五次多项式
-
- 表达式
- 代码实现
- 举例
- 总结
五次多项式
表达式
位置:
q ( t ) = k 0 + k 1 ( t − t 0 ) + k 2 ( t − t 0 ) 2 + k 3 ( t − t 0 ) t 3 + k 4 ( t − t 0 ) 4 + k 5 ( t − t 0 ) 5 (1) q(t)=k_0+k_1(t-t_0)+k_2(t-t_0)^2+k_3(t-t_0)t^3+k_4(t-t_0)^4+k_5(t-t_0)^5 \tag{1} q(t)=k0+k1(t−t0)+k2(t−t0)2+k3(t−t0)t3+k4(t−t0)4+k5(t−t0)5(1)
求一阶导数可以得到速度:
q ˙ ( t ) = k 1 + 2 k 2 ( t − t 0 ) + 3 k 3 ( t − t 0 ) 2 + 4 k 4 ( t − t 0 ) 3 + 5 k 5 ( t − t 0 ) 4 (2) \dot q(t)=k_1+2k_2(t-t_0)+3k_3(t-t_0)^2+4k_4(t-t_0)^3+5k_5(t-t_0)^4 \tag{2} q˙(t)=k1+2k2(t−t0)+3k3(t−t0)2+4k4(t−t0)3+5k5(t−t0)4(2)
求二阶导数可以得到加速度:
q ¨ ( t ) = 2 k 2 + 6 k 3 ( t − t 0 ) + 12 k 4 ( t − t 0 ) 2 + 20 k 5 ( t − t 0 ) 3 (3) \ddot q(t)=2k_2+6k_3(t-t_0)+12k_4(t-t_0)^2+20k_5(t-t_0)^3 \tag{3} q¨(t)=2k2+6k3(t−t0)+12k4(t−t0)2+20k5(t−t0)3(3)
特点:
- 加速度连续
- 可以定义起始和结束的位置、速度、加速度
计算
给定起始和结束的位置、速度、加速度以及轨迹时间 T T T,可以构造六个方程,解出五次多项式的6个系数。
满足的约束方程为:
q ( t 0 ) = q 0 , q ( t 1 ) = q 1 q ˙ ( t 0 ) = v 0 , q ˙ ( t 1 ) = v 1 q ¨ ( t 0 ) = a 0 , q ¨ ( t 1 ) = a 1 (4) q(t_0) = q_0 , \qquad q(t_1) = q_1 \\\dot q(t_0) = v_0, \qquad\dot q(t_1) = v_1 \\\ddot q(t_0) = a_0, \qquad\ddot q(t_1) = a_1 \tag{4} q(t0)=q0,q(t1)=q1q˙(t0)=v0,q˙(t1)=v1q¨(t0)=a0,q¨(t1)=a1(4)
把方程(4)结合(1)、(2)、(3)可以得到6个线性方程组,最终可以得到如下解:
T = t 1 − t 0 h = q 1 − q 0 k 0 = q 0 k 1 = v 0 k 2 = a 0 2 k 3 = 1 2 T 3 [ 20 h − ( 8 v 1 + 12 v 0 ) T − ( 3 a 0 − a 1 ) T 2 ] k 4 = 1 2 T 4 [ − 30 h + ( 14 v 1 + 16 v 0 ) T + ( 3 a 0 − 2 a 1 ) T 2 ] k 5 = 1 2 T 5 [ 12 h − 6 ( v 1 + v 0 ) T + ( a 1 − a 0 ) T 2 ] (5) \begin{aligned} &T = t_1 - t_0 \\ &h = q_1 - q_0 \\ &k_0 = q_0 \\ &k_1 = v0 \\ &k_2 = \frac{a_0}{2} \\ &k_3 = \frac {1}{2T^3} [20h − (8v_1 + 12v_0)T − (3a_0 − a_1)T^2] \\ &k_4 = \frac {1}{2T^4} [−30h + (14v_1 + 16v_0)T + (3a_0 − 2a_1)T^2] \\ &k_5 = \frac{1}{2T^5} [12h − 6(v_1 + v_0)T + (a_1 − a_0)T^2] \end{aligned} \tag{5} T=t1−t0h=q1−q0k0=q0k1=v0k2=2a0k3=2T31[20h−(8v1+12v0)T−(3a0−a1)T2]k4=2T41[−30h+(14v1+16v0)T+(3a0−2a1)T2]k5=2T51[12h−6(v1+v0)T+(a1−a0)T2](5)
代码实现
这里用python来实现五次多项式插值:
#!/usr/bin/python3
"""
Copyright © 2021 boldyoungster. All rights reserved.
@file Polynomial.py
@date: 11:06:12, February 28, 2021
"""
import numpy as np
import matplotlib.pyplot as plt
class PolynomialQuintic:
def __init__(self, t0, t1, q0, q1, v0=0.0, v1=0.0, a0=0.0, a1=0.0):
coeffs = self.__ComputeQuinticCoeffs(t0, t1, q0, q1, v0, v1, a0, a1)
self.poly = np.poly1d(coeffs[::-1])
@classmethod
def __ComputeQuinticCoeffs(cls, t0, t1, q0, q1, v0, v1, a0, a1):
T = t1 - t0
T2 = T * T
h = q1 - q0
k0 = q0
k1 = v0
k2 = 0.5 * a0
k3 = (20. * h - (8. * v1 + 12. * v0) * T -
(3 * a0 - a1) * T2) / (2. * T * T2)
k4 = (-30. * h + (14*v1 + 16*v0)*T+(3*a0 - 2*a1)*T2) / (2. * T2 * T2)
k5 = (12 * h - 6*(v1 + v0) * T + (a1 - a0) * T2) / (2 * T2 * T2 * T)
return (k0, k1, k2, k3, k4, k5)
if __name__ == "__main__":
t0, t1 = 0, 3.0
q0, q1 = 0, 1
v0, v1 = 0, 0
a0, a1 = 0, 0
poly = PolynomialQuintic(t0, t1, q0, q1,
v0, v1, a0, a1)
ts = np.linspace(t0, t1, 200)
qs = poly.poly(ts)
vs = poly.poly.deriv(1)(ts)
dvs = poly.poly.deriv(2)(ts)
plt.subplots_adjust(hspace=1)
plt.suptitle("QuinticPolynomial")
plt.subplot(311)
plt.plot(ts, qs)
plt.title("Position")
plt.subplot(312)
plt.plot(ts, vs)
plt.title("Velocity")
plt.subplot(313)
plt.plot(ts, dvs)
plt.title("Acceleration")
plt.savefig("./QuinticPolynomial.png")
plt.show()
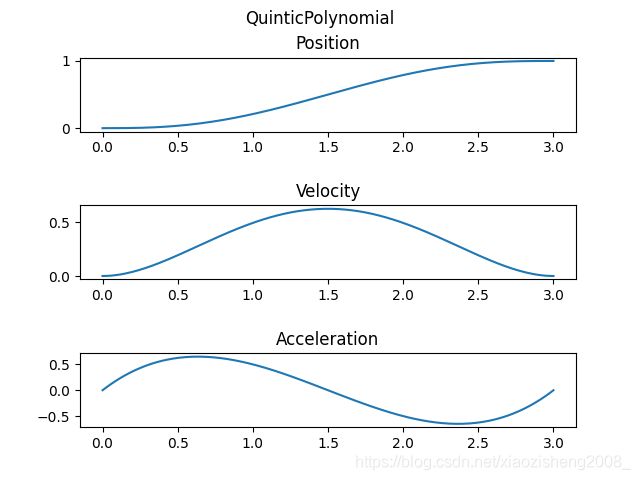
举例
t 0 = 0.0 , t 1 = 3.0 q 0 = 0.0 , q 1 = 1.0 v 0 = 0.0 , v 1 = 0.0 a 0 = 0.0 , a 1 = 0.0 t_0 = 0.0, \qquad t_1 = 3.0 \\q_0 = 0.0, \qquad q_1 = 1.0 \\v_0 = 0.0, \qquad v_1 = 0.0 \\a_0 = 0.0, \qquad a_1 = 0.0 t0=0.0,t1=3.0q0=0.0,q1=1.0v0=0.0,v1=0.0a0=0.0,a1=0.0
这段轨迹是从速度、加速度为0开始,再到速度、加速度为0停止,称作rest-to-rest,其轨迹形状如下:
总结
五次多项式是一种经常使用的插值方式,它可以保证加速度连续,可以定义轨迹两个端点的速度、加速度,有比较好的平滑性。