【python算法系列二】快速排序算法

快速排序的思想是：取数组中的一个数作为基准值，把所有小于基准值的数都放在它的一侧，再把所有大于基准值的数都放在它的另一侧。随后，对基准值左右两侧的数组分别进行快速排序。由此可以看出，快速排序的整个排序过程也是递归进行的。

快速排序的平均时间复杂度是 O(nlgn)，最好情况下的时间复杂度是 O(nlgn)。最坏情况下，快速排序的时间复杂度可能退化成 O(n2)，但这种情况很少见。它的空间复杂度是 O(nlgn)。它是一个不稳定的排序算法。如果使用得当，快速排序的速度可以达到归并排序和堆排序的数倍，所以快速排序是一种极其常用的算法。

以升序排序为例，快速排序的流程如下：

图 1：快速排序

一般情况下，我们取数组的第一个数作为基准进行快速排序。在第一步中，基准数为 5。可以看出，在第二行的数组中，比 5 小的元素：3、4、1、2，都被置于 5 的左侧，而比 5 大的元素则被置于 5 的右侧。这时，元素 5 在有序数组中的位置就确定了。

第三行中，我们再取左右两个无序数组的第一个数 3 和 6，分别作为它们的基准数，然后再次对数组进行分拆。分拆结束之后，3 和 6 在有序数组中的位置也确定了。

接下来，继续处理分拆出来的 4 个子数组：[1,2]、[4]、[]、[8,7]。其中，一个子数组只剩一个数，一个为空。这意味着 [4] 与 [] 已经完成了对自己的快速排序。而其他的两个子数组则需继续处理。全部处理完毕后，我们将得到一个完整的有序数组。

可以看出，快速排序也是通过这样的分治思想来排序的。关于它的分治思想我们之后会继续讲解。 

快速排序代码（基础版）

nums = [5,3,6,4,1,2,8,7]
def QuickSort(num):
    if len(num) <= 1: #边界条件
        return num
    key = num[0] #取数组的第一个数为基准数
    llist,rlist,mlist = [],[],[key] #定义空列表，分别存储小于/大于/等于基准数的元素
    for i in range(1,len(num)): #遍历数组，把元素归类到3个列表中
        if num[i] > key:
            rlist.append(num[i])
        elif num[i] < key:
            llist.append(num[i])
        else:
            mlist.append(num[i])
    return QuickSort(llist)+mlist+QuickSort(rlist) #对左右子列表快排，拼接3个列表并返回
print(QuickSort(nums))

运行程序，输出结果为：

[1,2,3,4,5,6,7,8]

在 QuickSort( ) 函数中，首先是边界条件：如果传入函数的列表长度小于等于 1，那么这一段列表必定是有序的，可以直接返回。如果不满足边界条件，则继续执行函数。先用 key 存储基准值，再定义 3 个列表存储小于基准数的元素 llist，大于基准数的元素 rlist 和等于基准数的元素 mlist。由于接下来 for 循环的范围不包括列表中的第一个数，所以对 mlist 初始化时，多加一个初始元素 key。

接下来的 for 循环把数组内的元素分别归入 3 个列表中。随后，再次调用 QuickSort( ) 函数，对 llist 和 rlist 进行排序。这样，llist 和 rlist 就是有序的了，而 mlist 内的元素刚好处于它们中间的连接部分。所以，排序完成后，把 llist、mlist、rlist 按顺序拼接到一起并输出。

这是实现快速排序的一种方式。但是，这样实现快速排序需要额外开辟空间给用于归类的列表。并且，相似的思路应用于其他的编程语言时效率较低。那么，该如何优化这个算法，使得数组可以原地排序呢？

我们需要优化的是把基准值移动到正确位置的那一部分代码。具体的移动流程如下：

我们用一个变量存储基准值。然后，再使用两个指针，一个从左往右遍历，一个从右往左遍历。开始遍历时，可以把基准值在数组中的位置，也就是第一个元素，视作一个没有元素的空位。

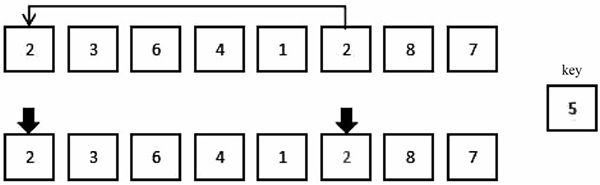
1) 如图 2 所示，移动右边的指针，一直到指针指向的元素小于基准值为止。

图 2：优化快速排序第一步

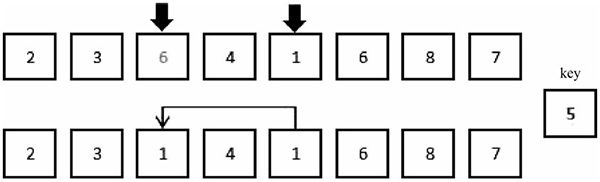
2) 如图 3 所示，把右边的指针指向的值 2 赋给左边的指针指向的位置。这时候，原来 2 所在的位置实际上是空出来的空位，空位在图 2 中用浅色字体表示。

图 3：优化快速排序第二步

 3) 如图 4 所示，移动左边的指针，等到它指向了一个大于等于基准值的数再停下。类似地，把左边的指针指向的值赋给右边的指针指向的位置。左边指针指向的位置成为空位。

图 4：优化快速排序第三步

 4) 重复以上步骤，不断地交替移动左边的指针和右边的指针，并赋值，如图 5 所示。

图 5：重复相似步骤

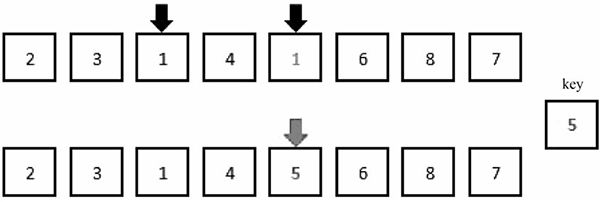
 5) 如图 6 所示，当左指针和右指针重合时，所有必要的移动都已经完成。左指针和右指针共同指向的位置就是基准值在有序数组中的位置。它的值大于它左侧的所有元素，并小于等于它右侧的所有元素（如果有相等的元素出现）。剩余的步骤为递归地排序左右子数组，直到全部数组排序完毕。

 图 6：当前范围内移动完成

快速排序代码（“原地”版）：

nums = [5,3,6,4,1,2,8,7]
def QSort(left,right):　　　　　　 #子数组第一个元素和最后一个元素在原数组中的位置
    if(left >= right):　　　　　　　#边界条件
        return
    l,r,key = left,right,nums[left]　#初始化左指针，右指针和基准值
    while(l < r):　　　　　　　　　 #调整元素位置
        while l < r and nums[r] >= key:
            r -= 1
        nums[l] = nums[r]
        while l < r and nums[l] < key:
            l += 1
        nums[r] = nums[l]
    nums[l] = key　　　　　　　　　 #把基准值赋给左指针和右指针共同指向的位置
    QSort(left,l-1)　　　　　　　　 #左侧数组排序
    QSort(l+1,right)　　　　　　　　#右侧数组排序
QSort(0,len(nums)-1)
print(nums)

运行程序，输出结果为：

[1,2,3,4,5,6,7,8]

这段代码没有采用直接将数组传入函数的方法，而是把子数组第一个和最后一个元素的位置传入函数中，从而确定循环范围。边界条件仍然不变：只有当子数组的长度（right-left+1）大于 1 时才继续递归。左指针 l 和右指针 r 初始化为第一个元素的下标和最后一个元素的下标，变量 key 用于存储基准值。

随后，while 循环就实现了前面图 2 ～图 6 展示的调整元素位置的过程。最后把两个子数组中间的位置赋值为 key，再对两个子数组分别排序。在函数外部，先调用 QSort( ) 函数对 nums 数组进行排序，再输出 nums 数组。 

 

【python算法系列一】冒泡排序算法采用重复遍历数组并依次比较相邻元素的方法来排序。由于在冒泡算法进行排序的过程中，最大数/最小数会慢慢“浮”到数组的末尾，所以算法由此命名。https://blog.csdn.net/m0_70372647/article/details/124736577【python算法系列二】快速排序算法快速排序的思想是：取数组中的一个数作为基准值，把所有小于基准值的数都放在它的一侧，再把所有大于基准值的数都放在它的另一侧。随后，对基准值左右两侧的数组分别进行快速排序。由此可以看出，快速排序的整个排序过程也是递归进行的。快速排序的平均时间复杂度是 O(nlgn)，最好情况下的时间复杂度是 O(nlgn)。最坏情况下，快速排序的时间复杂度可能退化成 O(n2)，但这种情况很少见。它的空间复杂度是 O(nlgn)。它是一个不稳定的排序算法。如果使用得当，快速排序的速度可以达到归并排序和堆排序的数倍，所以.https://blog.csdn.net/m0_70372647/article/details/124758205【python算法系列三】 希尔排序算法希尔排序，又叫“缩小增量排序”，是对插入排序进行优化后产生的一种排序算法。它的执行思路是：把数组内的元素按下标增量分组，对每一组元素进行插入排序后，缩小增量并重复之前的步骤，直到增量到达 1。一般来说，希尔排序的时间复杂度为 O(n1.3)～O(n2)，它视增量大小而定。希尔排序的空间复杂度是 O(1)，它是一个不稳定的排序算法。进行希尔排序时，元素一次移动可能跨越多个元素，从而可能抵消多次移动，提高了效率。下面是使用（数组长度/2）作为初始增量的升序希尔排序，每一轮排序过后，增量都缩小一半。1) 如https://blog.csdn.net/m0_70372647/article/details/124808637【python算法系列四】堆排序算法堆排序，就像它的名字一样，利用了堆的特性来进行排序。实现堆排序的思路是，把数组构建成一棵二叉树，并随着每次堆的变化更新堆顶的最大/最小值。堆排序的时间复杂度在所有情况下都是 O(nlgn)，它也是一个不稳定的算法。在开始编写堆排序的程序之前，我们首先要了解“堆”的概念。堆是一种数据结构，它是一种特殊的完全二叉树：如果这个堆是一个大顶堆（最大的元素在堆顶），那么每个节点上的元素都应该比它的子节点上的元素要大，最大的元素在根节点上；反之，如果是小顶堆，那么每个节点上的元素都应该比它的子节点小，最小的元素在根节https://blog.csdn.net/m0_70372647/article/details/124870580【python算法系列五】桶排序算法由于桶排序算法把每个数都放到合适的“桶”里进行排序，因此而得名。桶排序的算法原理可以理解为创建一个新的数组，把数依次放入合适的桶内，再按一定顺序输出桶。当每个桶的数据范围为 1 且数据皆为整数时，桶排序的时间复杂度在所有情况下都是 O(n)，因为它是一个线性的排序算法。但是，它的空间需求要视排序数据的范围而定，所以极有可能浪费很多空间。假设我们有 10 个整数 [1,1,3,19,35,49,50,5,10,16]，它们的范围在 1～50。如图 1 所示，我们建立 50 个存放数据的桶。图 1：https://blog.csdn.net/m0_70372647/article/details/124871084【python算法系列六】选择排序算法选择排序表示从无序的数组中，每次选择最小或最大的数据，从无序数组中放到有序数组的末尾，以达到排序的效果。选择排序的平均时间复杂度是O(n2)，最好情况下的时间复杂度和最坏情况下的时间复杂度都是 O(n2)。另外，它是一个不稳定的排序算法。选择排序的过程如下;1) 如图 1 所示，我们仍以递增排序的算法为例，先遍历未排序的数组，找到最小的元素。然后，把最小的元素从未排序的数组中删除，添加到有序数组的末尾。因为最小的元素是 1，所以 1 被添加到仍为空的有序数组末尾。图 1：选择并放置第一个元素https://blog.csdn.net/m0_70372647/article/details/124897318【python算法系列七】插入排序算法排序通常指把毫无规律的数据，按照一种特定的规律，整理成有序排列的状态。一般情况下，排序算法按照关键字的大小，以从小到大或从大到小的顺序将数据排列。排序算法是最基础也是最重要的算法之一，在处理大量数据时，使用一个优秀的排序算法可以节省大量时间和空间。因为不同的排序算法拥有不同的特点，所以我们应根据情况选择合适的排序算法。初级排序算法是指几种较为基础且容易理解的排序算法。初级排序算法包括插入排序、选择排序和冒泡排序 3 种。虽然它们的效率相对于高级排序算法偏低，但是在了解初级排序算法之后，再去学习相对复https://blog.csdn.net/m0_70372647/article/details/124907803【python算法系列八】归并排序算法相比起初级排序算法，高级排序算法往往有更加复杂的逻辑，但也会有更高的时间或空间效率。其中有些高级排序算法是由初级排序算法优化而来的。在处理大量数据时，高级排序算法的一般更加常用。本节教程介绍的第一种高级排序算法是归并排序。“归并”一词，意为“合并”。顾名思义，归并排序算法就是一个先把数列拆分为子数列，对子数列进行排序后，再把有序的子数列合并为完整的有序数列的算法。它实际上采用了分治的思想，之后我们会深度讲解分治思想。归并排序的平均时间复杂度是 O(nlgn)，最好情况下的时间复杂度是 O(nlg.https://blog.csdn.net/m0_70372647/article/details/124908304【Python算法系列九】 顺序查找算法定义查找的定义为：在一个数据元素集合中，通过一定的方法确定与给定关键字相同的数据元素是否存在于集合中。一般来说，如果查找成功，程序会返回数据的位置或相关信息；如果查找失败，则返回相应的提示。查找的方法可以分为两种：比较查找法与计算式查找法。比较查找法基于两种数据结构：线性表和树。查找的对象（一般是由同一类型的数据元素/记录构成的集合）又可以被称为查找表。查找还分为静态查找和动态查找。对查找表进行静态查找时，程序只进行查找并返回信息；进行动态查找时，在静态查找的基础上，还增加了增删查找表中.https://blog.csdn.net/m0_70372647/article/details/124931956【Python算法系列十】二分查找算法二分查找，也叫折半查找，是一种适用于顺序存储结构的查找方法。它是一种效率较高的查找方法，时间复杂度为 O(lgn)，但它仅能用于有序表中。也就是说，表中的元素需按关键字大小有序排列。二分查找用左右两个指针来标注查找范围。程序开始时，查找范围是整个线性表，左指针指向第一个元素，右指针指向最后一个元素；每一次循环过后，查找范围都缩小为原先的一半，直到左右指针重叠或者左指针处于右指针的右侧。因为每次缩小一半的范围，所以可以得出二分查找的时间复杂度为 O(lgn)。...https://blog.csdn.net/m0_70372647/article/details/124936085

【Python算法系列十一】二叉树的3种遍历方式二叉树的遍历是指从根结点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次。遍历二叉树的方法主要分 3 种：先序遍历、中序遍历和后序遍历：先序遍历指最先遍历节点本身，再遍历节点的左子树，最后遍历右子树的遍历方法；中序遍历指最先遍历节点的左子树，再遍历节点本身，最后遍历右子树的遍历方法；后序遍历指最先遍历节点的左子树，再遍历右子树，最后遍历节点本身的一种遍历方法。在图 1 中，L 是左子树，R 是右子树，D 当前节点。如果用这三个字母来表示 3 种遍历.https://blog.csdn.net/m0_70372647/article/details/124989895