二叉树遍历汇总
文章目录
-
- 二叉树遍历基础
-
- DFS
-
- 144. 二叉树的前序遍历
- 94. 二叉树的中序遍历
- 94. 二叉树的后序遍历
- BFS
-
- 102. 二叉树的层序遍历
- 637. 二叉树的层平均值
- 513. 找树左下角的值
- 199. 二叉树的右视图
- 116. 填充每个节点的下一个右侧节点指针
-
- 103. 二叉树的锯齿形层序遍历
- 构造二叉树
-
- 105. 从前序与中序遍历序列构造二叉树
- 二叉树遍历提升
-
-
- 124. 二叉树中的最大路径和
-
二叉树遍历基础
- 通过DFS实现,控制访问顺序即可,前中后是由根节点位置决定
前序(先序):根节点,左子树,右子树
中序:左子树,根节点,右子树
后序:左子树,右子树,根节点 - 二叉树层次遍历,通过BFS实现,具体借助队列
DFS
144. 二叉树的前序遍历
力扣传送门
思路:递归代码不难,这里就只给使用栈的代码
递归由于是函数的嵌套,所以每层的根节点,左节点,右节点都有记录,但迭代不一样,当我们不断往下的时候,我们只能记录一边的节点,也就是我们没法返回。即便遍历到了最后一个左节点,但我们无法回去遍历右节点,这时就需要借助堆栈来存储那些未被我们遍历的节点,
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> arr = new ArrayList();
Stack<TreeNode> sk = new Stack<TreeNode>();//借助栈
while (root != null || !sk.empty()) { //第一个节点未入栈,root != null
if (root == null) {
root = sk.pop();//出栈,即左边走完了走右边。
} else {
arr.add(root.val);//遇到就输出
sk.push(root.right);//同时把右边的节点入栈
root = root.left;//一直往左边
}
}
return arr;
}
}
94. 二叉树的中序遍历
力扣传送门
思路:递归代码不难,这里就只给使用栈的代码
public List<Integer> inorderTraversal(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
List<Integer> res = new ArrayList<>();
while(root != null && !stack.isEmpty()) {
if(root == null) {//左边一结束就出栈(往回走)
stack.pop();
res.add(root.val);
root = root.right//检查右边是否有元素,有的话改为当前元素,走下边的操作
} else {
stack.push(root);//一直往左边,遇到元素就入栈
root=root.left;
}
}
return res;
}
94. 二叉树的后序遍历
力扣传送门
思路一:递归代码不难,这里就只给使用栈的代码,按前序遍历反方向,即一直向右,并把左边的元素入堆栈。这样得到的结果为根-右-左,接着反转数组,结果为左-右-根,也就是后序遍历结果
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
Stack<TreeNode> stack = new Stack<TreeNode>();
//反转数组也可用队列实现,也就是元素不添加到队尾,而是添加到队头
LinkedList<Integer> res = new LinkedList<>();
while(root != null || !stack.isEmpty()) {
if(root == null) {
root = stack.pop();
} else {
res.addFirst(root.val);//队头插入
stack.push(root.left);//左边入栈
root = root.right;//一直往右边
}
}
return res;
}
}
思路二:按左-右-根顺序入栈,当出栈节点的左右都为null,则保存节点值。其中,遍历当前节点时(node),把左右节点入栈后,把当前节点与左右节点的联系断开,即node.left=null,node.right=null,这样出栈元素才不会陷入死循环,把每个节点当成独立节点。
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
Stack<TreeNode> stack = new Stack<TreeNode>();
LinkedList<Integer> res = new LinkedList<>();
if(root == null) return res;
stack.push(root);
while(!stack.isEmpty()) {
TreeNode node = stack.peek();
if(node.left == null && node.right ==null) {
res.add(stack.pop().val);
}
if(node.right != null) {
stack.push(node.right);
node.right =null;
}
if(node.left !=null) {
stack.push(node.left);
node.left =null;
}
}
return res;
}
}
BFS
102. 二叉树的层序遍历
力扣传送门
思路:层序遍历
由于每层节点归为一数组,那遍历时就需要把握每层的节点个数,可通过计数或者队列的长度来实现。
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if(root == null) return res;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
int count = 1;
while(!queue.isEmpty()) {
int loop = count;
count = 0;//记录每层节点个数,或者调用队列的size
List<Integer> list = new ArrayList<>();
while(loop-- > 0) {
TreeNode tmp = queue.poll();
list.add(tmp.val);
if(tmp.left != null) {
queue.add(tmp.left);
count++;
}
if(tmp.right != null) {
queue.add(tmp.right);
count++;
}
}
res.add(list);
}
return res;
}
637. 二叉树的层平均值
力扣传送门
思路:层次遍历,计算每层的值/每层节点个数,每层节点的个数等价于遍历每层时队列长度。
class Solution {
private LinkedList<TreeNode> queue = new LinkedList<>();
private List<Double> list = new ArrayList<>();
public List<Double> averageOfLevels(TreeNode root) {
if (root == null) return null;
queue.add(root);
while (!queue.isEmpty()) {
int num = queue.size();//队列长度即为当前层节点个数
double sum =0;
for (int i = 0; i < num; i++) {
TreeNode node = queue.poll();
sum += node.val;
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
list.add(sum/num);
}
return list;
}
}
513. 找树左下角的值
力扣传送门
思路:层次遍历
最后一层的第一个节点即为答案,虽然没法确定什么时候是最后一层,但只要每次遍历一层,就记录第一个值,那么最后一次记录即为答案。也就是不断将每一层的第一个节点的值赋值给变量ans,结束遍历时,ans即为所求
class Solution {
LinkedList<TreeNode> queue = new LinkedList<>();
private int ans;
public int findBottomLeftValue(TreeNode root) {
queue.add(root);
while (!queue.isEmpty()) {
int len = queue.size();
for (int i = 0; i < len ; i++) {
TreeNode node = queue.poll();
if(i==0) ans = node.val;
if (node.left != null) queue.add(node.left);
if (node.right != null) queue.add(node.right);
}
}
return ans;
}
}
199. 二叉树的右视图
https://leetcode.cn/problems/binary-tree-right-side-view/
class Solution {
private List<Integer> res;
public List<Integer> rightSideView(TreeNode root) {
//每次只返回右边的节点---说明只需要往右边递归即可---错误
//题目是说从右往左看,第一眼看到的节点,例如[1,2]的答案不是1
res = new ArrayList<>();
//思路:层序遍历,每一层的最后一个点。
Queue<TreeNode> q = new LinkedList<>();
q.add(root);
while(!q.isEmpty()) {
int size = q.size();
while(size-- > 0) {
TreeNode node = q.poll();
if(node != null) {
if(size == 0) {
res.add(node.val);
}
if(node.left != null) {
q.add(node.left);
}
if(node.right != null) {
q.add(node.right);
}
}
}
}
return res;
}
}
dfs:链接
116. 填充每个节点的下一个右侧节点指针
https://leetcode.cn/problems/populating-next-right-pointers-in-each-node/
class Solution {
public Node connect(Node root) {
if(root == null) return root;
//层序遍历
Queue<Node> q = new LinkedList<Node>();
q.add(root);
while(!q.isEmpty()) {
//遍历每一层节点,通过指针的移动实现节点的拼接
int size = q.size();
Node prev = q.poll();
if(prev.left != null) q.add(prev.left);
if(prev.right != null) q.add(prev.right);
for(int i = 1; i < size; i++) {
Node tmp = q.poll();
prev.next = tmp;
prev = tmp;
if(tmp.left != null) q.add(tmp.left);
if(tmp.right != null) q.add(tmp.right);
}
}
return root;
}
}
优化:dfs,见官方
103. 二叉树的锯齿形层序遍历
https://leetcode.cn/problems/binary-tree-zigzag-level-order-traversal/
easy
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
boolean flag = true;
List<List<Integer>> res = new ArrayList<>();
if(root == null) return res;
//层序遍历
Queue<TreeNode> qe = new LinkedList<>();
qe.add(root);
while(!qe.isEmpty()) {
Integer size = qe.size();
//使用数组来存放每一层
Integer[] arr = new Integer[size];
if(flag){
//正向遍历
for(int i = 0; i < size; i++) {
TreeNode tmp = qe.poll();
arr[i] = tmp.val;
if(tmp.left != null) qe.add(tmp.left);
if(tmp.right != null) qe.add(tmp.right);
}
} else {
//反向遍历
for(int i = size - 1; i >= 0; i--) {
TreeNode tmp = qe.poll();
arr[i] = tmp.val;
if(tmp.left != null) qe.add(tmp.left);
if(tmp.right != null) qe.add(tmp.right);
}
}
res.add(Arrays.asList(arr));
flag = !flag;
}
return res;
}
}
构造二叉树
必须有中序结果才能构建二叉树
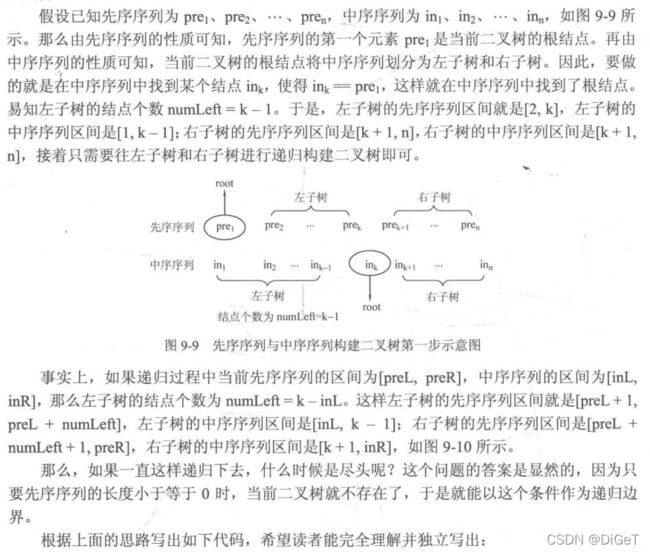
105. 从前序与中序遍历序列构造二叉树
力扣传送门
思路:先序中序遍历特点,具体看《算法笔记》—胡凡
理解书内的思路即可,具体实现可以不用那么复杂,因为书里的区间下标比较复杂,这里的前序数组其实可以不用转化为区间。
private int count = 0;//用于前序数组遍历
public TreeNode buildTree(int[] preorder, int[] inorder) {
return dfs(preorder,inorder,0,inorder.length - 1);
}
public TreeNode dfs(int[] pre, int[] in, int start, int end) {
//如果区间小于0则遍历结束
if(start > end) return null;
//前序当前节点做根节点
TreeNode node = new TreeNode(pre[count++]);
//查找中序节点,从而定位左右子树区间
int mid = 0;
for(int i = start; i <= end; i++) {
if(node.val == in[i]) {
mid = i;
break;
}
}
//左右子树构建
node.left = dfs(pre,in,start,mid-1);
node.right = dfs(pre,in,mid+1,end);
return node;
}
二叉树遍历提升
124. 二叉树中的最大路径和
https://leetcode.cn/problems/binary-tree-maximum-path-sum/
虽然是困难题,但不难,因为自己手敲完成时,超过100%很惊喜
- 思路就是后序遍历,先从左右两边获取最大值,然后与当前节点做判断。只有左右两边获得的值大于,才有必要加入当前节点。
- 然后使用一个max变量,记录当前节点的最大值,因为每个节点都可作为二叉树中的最大路径和的出发点。
- 最后再返回给上一层,注意这里返回就不能返回当前节点的最大值了,因为当前节点可能包含了左右子树,对于返回去的节点来说就是两条路径了。应该返回最大的一边,也可能是两边都小于0,直接返回当前节点。
class Solution {
private int max = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
dfs(root);
return max;
}
public int dfs(TreeNode root) {
if(root == null) {
return 0;
}
int a = dfs(root.left);
int b = dfs(root.right);
int tmp = 0;
if(a > 0) {
tmp+=a;
}
if(b > 0) {
tmp+=b;
}
//当前节点所能获得的最大值
tmp = tmp + root.val;
//记录每次的最大值
if(max < tmp) {
max = tmp;
}
//但是返回时只能返回一边,且取两边中大的那一边(当然前提要大于0,不然直接返回本身)
tmp = Math.max(a,b);
return tmp > 0 ? root.val + tmp : root.val;
}
}