【老生谈算法】基于matlab3机9节点系统的暂态稳定计算程序设计与算法原理（论文+程序源码）——暂态稳定计算

3机9节点系统的暂态稳定计算程序设计与算法原理

大家好，今天给大家介绍基于matlab3机9节点系统的暂态稳定计算程序设计与算法原理（论文+程序源码）。

文章目录：

1、项目简介

1. 本程序是基于隐式梯形积分法的暂态稳定分析程序，采用IEEE 3机9节点模型，对其在pt时刻7号节点发生三相短路故障，并在ct时刻将故障切除(断开5号节点和7号节点之间的线路)进行仿真，最后绘出2号和1号发电机的功角差(δ21)与时间的关系曲线。发电机模型采用三阶模型，忽略阻尼，电枢电阻取为零；励磁系统仅有量测和放大环节，忽略反馈和电压调节器；负荷采用恒定阻抗负荷。程序是在Matlab R2009b上调试和运行的。

---

2、难度指数

本项目难度：中等难度
适用场景：相关题目的毕业设计及相关领域的应用研究

---

3、运行环境：

环境配置：
本项目所使用的MATLAB版本为Matlab R2009b
注：可适配绝大部分matlab版本
项目技术：
隐式梯形积分法+暂态稳定分析+发电机模型+三阶模型+潮流计算等等

---

4、项目详解：

提示：以下为项目的详细介绍，项目源码及项目设计文档下载地址见文末。

4.1模型推导及相关公式
4.1.1发电机模型
发电机采用三阶模型，其隐式梯形积分法推导如下：
由发电机转子运动方程

式中，=w-1，TJ和t单位为s，wB=314rad/s，其他变量均为标幺值。根据梯形积分法则，得tn~tn+1时步的差分方程为

其中



由发电机转子绕组暂态方程

根据梯形积分法则差分化，得

式中

由发电机定子电压方程

将其转化为xy坐标下为



4.1.2 励磁系统模型
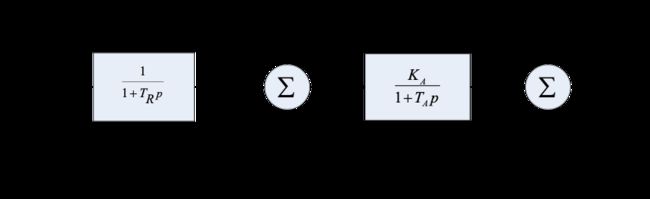
励磁系统传递函数框图如图1所示：

由图1传递函数，可得励磁系统基本方程式为

根据梯形积分法则，写出相应差分方程并整理得

联立式13、10和19，就得到系统的差分方程(略去下标n+1)

式中参数运用前面公式可求得。

4.1.3 负荷模型
负荷模型看作是恒定阻抗，并入导纳矩阵。负荷的等值并联导纳为

4.1.4 消去网络模型
由于只有发电机端节点注入电流不为零，其他节点的注入电流全为零，因此可消去网络除发电机外的其他节点。消去过程如下：

其中下标n代表发电机节点，r代表其余节点。

至此网络差分方程推导完毕，即式20和25。对于N机系统有6N个未知量，也有6N个方程，联立此方程运用牛顿迭代法即可求解。

4.2程序流程图
本程序的主要流程图如下图所示：

故障在t=pt时刻加入，并在t=ct时刻清除故障，如果系统稳定令t=t+1继续进行牛顿法迭代，直到系统失稳，最后绘出发电机功角差与时间的关系曲线。

4.3变量说明
LN：支路参数。格式如下：

其中线路状态为0或1。0代表支路是线路，1代表支路是变压器。
GEN：发电机参数。格式如下：

其中发电机节点类型为0或1。0代表节点是PQ节点，1代表节点是PV节点。
LOAD：负荷参数。格式如下：

ROTOR：发电机暂态参数。格式如下：

EXC：励磁系统参数。格式如下：

sp：定常参数。格式如下：

nsp：非定常参数。格式如下：

其他变量定义如下：

4.4输出结果
系统故障在t=pt时刻加入，故障是7号节点三相短路，在ct时刻将故障切除，断开5号和7号节点之间的支路。Matlab仿真结果如下：

图是当pt=0.05s，ct=0.167s时2号和3号发电机分别与1号发电机之间的功角差曲线图。由图可知，在0~2.4s的时间内，任何一个功角差均没有超过180，系统是暂态稳定的；但2.4s以后就失去稳定了。

图是当pt=0.05s，ct=0.168s时2号和3号发电机分别与1号发电机之间的功角差曲线图。由图所示，系统在2s内就失去了稳定。

进一步增加故障清除时间，得到下图所示图形，其中pt=0.05s，ct=0.4s。可以看出系统在清除故障前就已经失去了稳定。

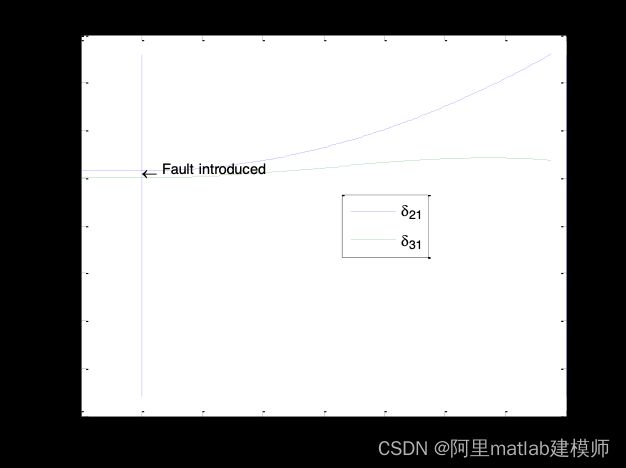
由此可以得出以下结论：系统发生故障时，随着故障切除时间的推迟，系统的暂态稳定时间范围越来越小。因此当系统发生故障时，尽快地检测并清除故障是保证系统暂态稳定的首要条件，清除故障后如果采取一些稳定措施，系统恢复稳态的可能性就会增加。

4.5部分程序源码

function x=nagauss2(a,b)
%用途：列主元Gauss消去法解线性方程组ax=b
%格式：x=nagauss2(a,b,flag) a为系数矩阵，b为右端列向量,x为解向量
n=length(b);a=[a,b];
for k=1:(n-1)
%选主元
[ap,p]=max(abs(a(k:n,k)));
p=p+k-1;
if p>k
    t=a(k,:);a(k,:)=a(p,:);a(p,:)=t;
end   
%消元
a((k+1):n,(k+1):(n+1))=a((k+1):n,(k+1):(n+1))-a((k+1):n,k)/a(k,k)*a(k,(k+1):(n+1));
a((k+1):n,k)=zeros(n-k,1);   
end
%回代
x=zeros(n,1);
x(n)=a(n,n+1)/a(n,n);
for k=n-1:-1:1
    x(k,:)=(a(k,n+1)-a(k,(k+1):n)*x((k+1):n))/a(k,k);
end
function [nsp]=parametersolve(sp,nsp,EXC,ROTOR,U)
%%%%%%%%%%%%%%%求解非定常参数子程序%%%%%%%%%%%%
%%%sp:[adita,Pm0;aw;aq1;aEf_1;aq2;aEf;aUTR;Uref;Eq0];
%%%nsp:[IG0;Eq0_1;dita0;Pe0;UTR0;Ef0;Id0;dw0;VR;bdita_1;bEf_1;bq;bUTR,bEf];
aw=sp(3,:);aEf=sp(7,:);Pm0=sp(2,:);aUTR=sp(8,:);
Uref=sp(9,:);aq1=sp(4,:);Id=nsp(7,:);Pe=nsp(4,:);
UTR=nsp(5,:);dw=nsp(8,:);Ef=nsp(6,:);Eq_1=nsp(2,:);
Ef0=sp(10,:);VR=nsp(9,:);dita=nsp(3,:);adita=sp(1,:);
for i=1:3
    bw(i)=aw(i)*(Pm0(i)-Pe(i))+dw(i);
    bdita(i)=adita(i)*dw(i)+dita(i);
    bdita_1(i)=(bw(i)+aw(i)*Pm0(i))*adita(i)+bdita(i);
    bUTR(i)=aUTR(i)*(-2*UTR(i)+ abs(U(i)))+UTR(i);
    bEf(i)=aEf(i)*(2*EXC(i,3)*Uref(i)-2*VR(i)-EXC(i,3)*UTR(i))+VR(i);
    bEf_1(i)=bEf(i)-aEf(i)*EXC(i,3)*bUTR(i)+Ef0(i);
    bq(i)=aq1(i)*(Ef(i)-2*Eq_1(i)-(ROTOR(i,3)-ROTOR(i,4))*Id(i))+Eq_1(i);
end
nsp(10,:)=bdita_1;nsp(11,:)=bEf_1;nsp(12,:)=bq;nsp(13,:)=bUTR;nsp(14,:)=bEf;
function [J,F]=Jform(sp,U,nsp,ROTOR,Y)
%%%形成雅可比矩阵子程序%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%sp:[adita,Pm0;aw;aq1;aEf_1;aq2;aEf;aUTR;Uref;Eq0];
%%nsp:[IG0;Eq0_1;dita0;Pe0;UTR0;Ef0;Id0;dw0;VR;bdita_1;bEf_1;bq;bUTR];
I=nsp(1,:);dita=nsp(3,:);aw=sp(3,:);aq1=sp(4,:);adita=sp(1,:);bq=nsp(12,:);
aq2=sp(6,:);aEf_1=sp(5,:);Eq_1=nsp(2,:);bdita_1=nsp(10,:);bEf_1=nsp(11,:);
Ix=real(I);Iy=imag(I);Xd_1=ROTOR(:,4);Xq=ROTOR(:,8);
Ux=real(U);Uy=imag(U);unit=1;a=[0,0,0];b=[0,0,0];J=zeros(18,18);F=zeros(18,1);
for i=1:3
    J(6*(i-1)+1,6*(i-1)+1)=unit;
    J(6*(i-1)+1,6*(i-1)+3)=adita(i)*aw(i)*Ix(i);
    J(6*(i-1)+1,6*(i-1)+4)=adita(i)*aw(i)*Iy(i);
    J(6*(i-1)+1,6*(i-1)+5)=adita(i)*aw(i)*Ux(i);
    J(6*(i-1)+1,6*(i-1)+6)=adita(i)*aw(i)*Uy(i);
    J(6*(i-1)+2,6*(i-1)+1)=-aq2(i)*(Ix(i)*cos(dita(i))+Iy(i)*sin(dita(i)));
    J(6*(i-1)+2,6*(i-1)+2)=unit;
    J(6*(i-1)+2,6*(i-1)+3)=-aq1(i)*aEf_1(i)*Ux(i)/abs(U(i));
    J(6*(i-1)+2,6*(i-1)+4)=-aq1(i)*aEf_1(i)*Uy(i)/abs(U(i));
    J(6*(i-1)+2,6*(i-1)+5)=-aq2(i)*sin(dita(i));
    J(6*(i-1)+2,6*(i-1)+6)=aq2(i)*cos(dita(i));
    J(6*(i-1)+3,6*(i-1)+1)=(Ux(i)-Xd_1(i)*Iy(i))*sin(dita(i))-(Uy(i)+Xd_1(i)*Ix(i))*cos(dita(i));
    J(6*(i-1)+3,6*(i-1)+2)=unit;
    J(6*(i-1)+3,6*(i-1)+3)=-cos(dita(i));
    J(6*(i-1)+3,6*(i-1)+4)=-sin(dita(i));
    J(6*(i-1)+3,6*(i-1)+5)=-Xd_1(i)*sin(dita(i));
    J(6*(i-1)+3,6*(i-1)+6)=Xd_1(i)*cos(dita(i));
    J(6*(i-1)+4,6*(i-1)+1)=(Ux(i)-Xq(i)*Iy(i))*cos(dita(i))+(Uy(i)+Xq(i)*Ix(i))*sin(dita(i));
    J(6*(i-1)+4,6*(i-1)+2)=0;
    J(6*(i-1)+4,6*(i-1)+3)=sin(dita(i));
    J(6*(i-1)+4,6*(i-1)+4)=-cos(dita(i));
    J(6*(i-1)+4,6*(i-1)+5)=-Xq(i)*cos(dita(i));
    J(6*(i-1)+4,6*(i-1)+6)=-Xq(i)*sin(dita(i));
    for j=1:3
        J(6*(i-1)+5,6*(j-1)+3)=-real(Y(i,j));
        J(6*(i-1)+5,6*(j-1)+4)=imag(Y(i,j));
        J(6*(i-1)+6,6*(j-1)+3)=-imag(Y(i,j));
        J(6*(i-1)+6,6*(j-1)+4)=-real(Y(i,j));
    end
    J(6*(i-1)+5,6*(i-1)+5)=unit;
    J(6*(i-1)+6,6*(i-1)+6)=unit;
    F(6*(i-1)+1,1)=dita(i)+adita(i)*aw(i)*(Ux(i)*Ix(i)+Uy(i)*Iy(i))-bdita_1(i);
    F(6*(i-1)+2,1)=Eq_1(i)-aq1(i)*(aEf_1(i)*abs(U(i))+bEf_1(i))-aq2(i)*(Ix(i)*sin(dita(i))-Iy(i)*cos(dita(i)))-bq(i);
    F(6*(i-1)+3,1)=Eq_1(i)-(Ux(i)-Xd_1(i)*Iy(i))*cos(dita(i))-(Uy(i)+Xd_1(i)*Ix(i))*sin(dita(i));
    F(6*(i-1)+4,1)=(Ux(i)-Xq(i)*Iy(i))*sin(dita(i))-(Uy(i)+Xq(i)*Ix(i))*cos(dita(i));
    for j=1:3
        
        a(i)=a(i)+real(Y(i,j))*Ux(j)-imag(Y(i,j))*Uy(j);
        b(i)=b(i)+real(Y(i,j))*Uy(j)+imag(Y(i,j))*Ux(j);
        
    end
    F(6*(i-1)+5,1)=Ix(i)-a(i);
    F(6*(i-1)+6,1)=Iy(i)-b(i);
end

---

5、源码下载：

本项目及一些精选的matlab暂态稳定和潮流计算项目源码如下，有需要的朋友可以点击进行下载

序号	matlab人脸识别项目（点击下载）
1 (本项目源码)	基于matlab的3机9节点系统暂态稳定计算程序源码+项目设计文档_暂态稳定计算_发电机模型_系统稳态恢复_matlab
2	L NEWPeiWangChaoLiu配电网潮流计算matlab程序_matlab
3	用简化梯度法进行电力系统最优潮流计算_matlab源码
4	内点法进行最优潮流计算的程序_可以修改目标函数来进行其他不同条件下的最优潮流计算_matlab源码
5	将数学规划原理和常规潮流计算相有机结合_形成的带有最优乘子的牛顿算法_最优潮流_matlab
6	电力系统最优潮流程序_可以应用于电力市场下的最优潮流计算_适合电力系统专业的同仁使用_matlab源码
7	电力系统仿真计算软件包_包括潮流计算_最优潮流计算等_matlab
8	matlab识别电力系统网路_求出其中树的数目_求电力系统中的潮流计算_求电力系统中的灵敏度_matlab源码
9	My_NRflow_Matlab潮流计算_电力研究_PowerLosses
10	MATLAB潮流计算和最优潮流计算的程序_毕业设计
11	潮流计算万能程序，能够计算潮流，网络潮流程序编写的不错，matlab源码
12	多目标无功优化算法_采用遗传算法_非支配排序_前推回代潮流计算_NSAGA_matlab
13	ar模型_多项式乘法_潮流计算_NSGA_场景削减_MATLAB编程代码