leetcode：72. 编辑距离

题目来源

• leetcode

题目描述

class Solution {
public:
    int minDistance(string word1, string word2) {

    }
};

题目解析

什么叫做编辑距离

编辑距离是用来量化两个字符串的相似度的。

所谓编辑距离就是指，将一个字符串转换成另一个字符串，需要的最少编辑操作次数(比如增加一个字符、删除一个字符、替换一个字符)

• 编辑距离越大，说明两个字符串的相似程度越小；
• 编辑距离越小，说明两个字符串的相似程度越大。

对于两个完全相同的字符串来说，编辑距离就是0.

根据所包含的编辑，编辑距离有多种不同的计算方式，比较著名的有

• 莱文斯坦距离：
  • 允许增加、删除、替换字符这三个编辑操作
  • 莱温斯坦距离的大小，表示两个字符串差异的大小
• 最长公共子串长度：
  • 只允许增加、删除字符这两个编辑操作。
  • 最长公共子串的大小，表示两个字符串相似程度的大小。
• 汉明距离：
  • 只允许替换操作，因此只适用于两个相等长度的字符串。

比如，两个字符串 mitcmu 和mtacnu 的莱文斯坦距离是 3，最长公共子串长度是 4。

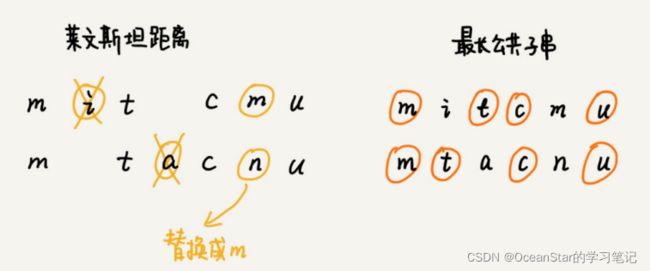
本题要求计算莱文斯坦距离

• 整个求解过程，涉及多个决策阶段：
  • 我们需要依次考察一个字符串中的每个字符，跟另一个字符串中的字符是否匹配
  • 匹配的话如何处理，不匹配的话又如何处理。
• 所以，这个问题符合多阶段决策最优解模型。

回溯

回溯是一个递归处理的过程：

• 如果word1[i]和word2[j]匹配，我们递归考察word1[i+1]和word2[j+1]。
• 如果word1[i]和word2[j]不匹配，那我们有多种处理方式可选：
  • 可以删除word1[i]，然后递归考察word1[i+1]和word2[j]
  • 可以删除word2[j]，然后递归考察word1[i]和word2[j+1]
  • 可以在word1[i]前面添加一个跟word2[j]相同的字符，然后递归考察word1[i]和word2[j+1]
  • 可以在word2[j]前面添加一个跟word1[i]相同的字符，然后递归考察word1[i+1]和word2[j]
  • 可以将word1[i]替换成word2[j]，或者将word2[j]替换成word1[i]，然后递归考察 word1[i+1]和word2[j+1]

class Solution {
    int miDist = INT32_MAX; //存储结果
    void lwstBT(std::string &a, std::string &b, int i, int j, int edist){
        if(i == a.size() || j  == b.size()){
            if(i < a.size()){
                edist += (int)(a.size() - i);
            }
            if(j < b.size()){
                edist += (int)(b.size() - j);
            }
            miDist = std::min(miDist, edist);
            return;
        }

        if(a[i] == b[j]){   // 两个字符匹配
            lwstBT(a, b, i + 1, j + 1, edist);
        }else{//两个字符不匹配
            lwstBT(a, b, i + 1,   j ,    edist + 1);  // 删除 a[i] 或者 b[j] 前添加一个字符
            lwstBT(a, b,   i,     j + 1, edist + 1);   // 删除 b[j] 或者 a[i] 前添加一个字符
            lwstBT(a, b, i + 1, j + 1, edist + 1);    // 将 a[i] 和 b[j] 替换为相同字符
        }
    }
public:
    int minDistance(string word1, string word2){
        lwstBT(word1, word2, 0,0, 0);
        return miDist;
    }
};

根据回溯算法的代码实现，我们可以画出递归树，看是否存在重复子问题。如果存在重复子问题，那我们就可以考虑是否能用动态规划来解决；如果不存在重复子问题，那回溯就是最好的解决方法。

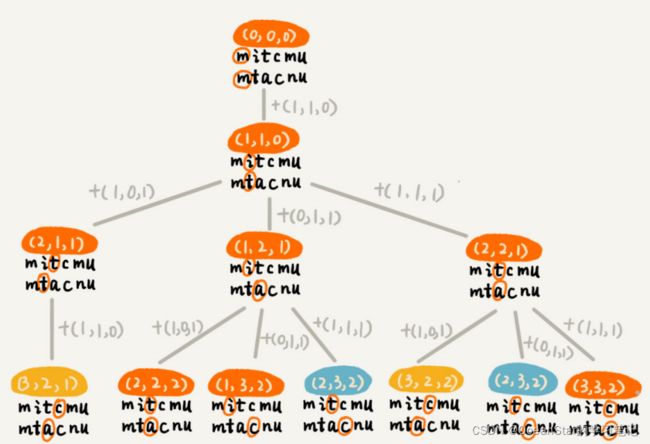
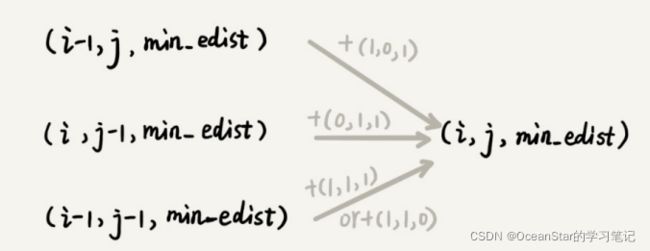
在递归树中，每个节点代表一个状态，状态包含三个变量$(i，j，edist)$，其中，edist表示处理到$a[i]$和$b[j]$时，已经执行的编辑操作的次数。

在递归树中，$(i，j)$两个变量重复的节点很多，比如$(3，2)$和$(2，3)$。对于$(i，j)$相同的节点，我们只需要考虑保留edist最小的，继续递归处理就可以了，剩下的节点都可以舍弃。所以，状态就从$(i，j，edist)$变成了$(i，j，mindist)$，其中mindist表示处理到$a[i]$和$b[j]$，已经执行的最少编辑次数。

这里的动态递归跟矩阵最短路径很相似，在矩阵最短路径中，到达状态(i，j)只能通过(i-1，j)或者(i，j-1)两个状态转移过来，而字符编辑距离状态(i，j)可能从(i-1，j)，(i，j-1)，(i-1，j-1)三个状态中的任意一个转移过来。

样本对应模型

样本对应模型往往是根据结尾位置来做可能性划分的

• 定义$dp[i][j]$表示：s1只拿前i个字符，编辑成s2的前j个字符的最小代价

举个例子

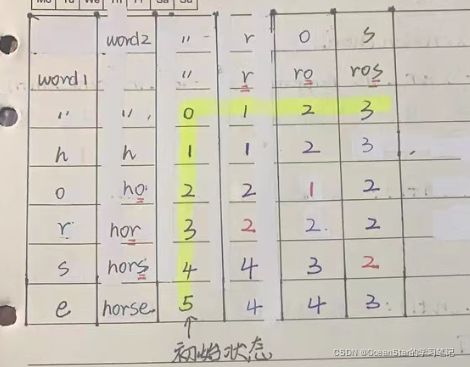
（1）初始化表

• $dp[0][0]$表示空串编辑成空串的最小代价
• $dp[0][\mathrm{1...}]$表示s1为空串时，编辑成s2的前j个前缀的最小代价
  • 空串—>非空串，那么只能添加字符
• $dp[\mathrm{1...}][0]$表示s2为空串时，取s1的前i个字符能编辑成空串的最小代价
  • 非空串—>空串，那么只能删除字符

（2）中间情况怎么决策

• 假设前面的都解决了，现在正在考虑最后一个字符
• 现在只要对s1的最后一个字符做些什么，就能将s1编辑成s2了。那么对于s1能做哪些动作呢？
  • 可能性1：s1的前i-1个字符已经变成了s2的前j个字符，现在只需要删除s1的第i个字符即可
  • 可能性2：s1的前i个字符已经变成了s2的前j-1个字符，现在只需要加上s2的第j个字符
  • 可能性3： s1、s2的最后一个字符相等，那么只需要s1的前i-1个字符变成s2的前j-1个字符即可
  • 可能性4：s1、s2的最后一个字符不相等，那么只需要s1的前i-1个字符变成s2的前j-1个字符即可，最后一个字符串做替换
  • 可能性3和可能性4只有一个能够成立

class Solution {

private:
    int minCost(std::string s1, std::string s2, int ac, int dc, int rc){
        int M = s1.size(), N = s2.size() ;
        std::vector<std::vector<int>> dp(M + 1, std::vector<int>(N + 1, 0));
        dp[0][0] = 0;
        for (int i = 1; i <= M; ++i) {
            dp[i][0] = dc * i;  //非空串--->空串，只能删除字符
        }
        for (int j = 1; j <= N; ++j) {
            dp[0][j] = ac * j;  //空串--->非空串，只能添加字符
        }

        for (int i = 1; i <= M; ++i) {
            for (int j = 1; j <= N; ++j) {
                if(s1[i - 1] == s2[j - 1]){
                    dp[i][j] = dp[i - 1][j - 1];
                }else{
                    dp[i][j] = dp[i - 1][j - 1] + rc;
                }

                dp[i][j] = std::min(dp[i][j - 1] + dc, dp[i][j]);
                dp[i][j] = std::min(dp[i - 1][j] + ac, dp[i][j]);
            }
        }

        return dp[M][N];
    }

public:
    int minDistance(string word1, string word2){
        return minCost(word1, word2, 1,1, 1);
    }
};

推导转移方程

（1）定义状态：

• f[i][j]表示将word1的前i个字符变成word2的前j个字符所需要进行的最少操作次数
• 需要考虑 word1 或 word2 一个字母都没有，即全增加/删除的情况，所以预留dp[0][j]和 dp[i][0]

（2）状态转移方程：对于f[i][j]，考虑word1的第i个字符与word2的第j个字符，分为两种情况：

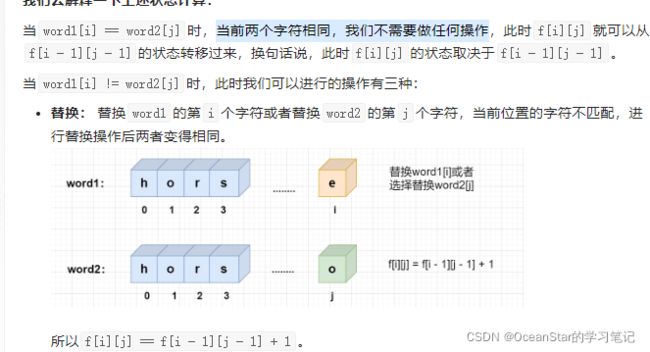
• word1[i] == word2[j]，则f[i][j] == f[i - 1][j - 1]
• word1[i] != word2[j]，我们有三种选择，替换、删除、插入：
  • 替换： 替换word1的第i个字符或者替换word2的第j个字符，则f[i][j] == f[i - 1][j - 1] + 1；
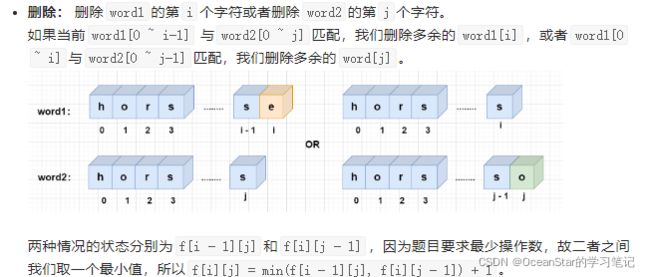
  • 删除： 删除word1的第i个字符或者删除word2的第j个字符，则f[i][j] = min(f[i - 1][j], f[i][j - 1]) + 1;
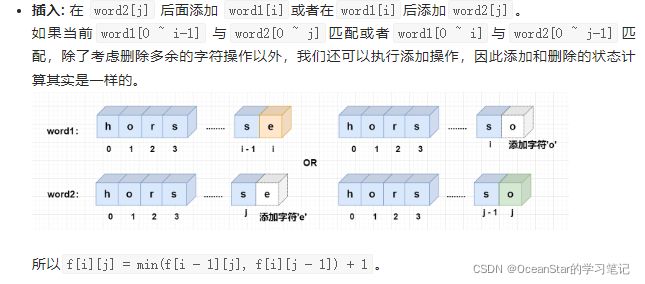
  • 插入: 在 word2[j] 后面添加 word1[i]或者在word1[i]后添加word2[j]，则f[i][j] = min(f[i - 1][j], f[i][j - 1]) + 1;

（3）计算顺序：

• 按顺序计算，当计算 dp[i][j] 时，dp[i - 1][j] ， dp[i][j - 1] ，dp[i - 1][j - 1]均已经确定了

（4）dp如何初始化：从一个字符串变成空字符串，非空字符串的长度就是编辑距离

for (int i = 0; i <= len1; i++) {
    dp[i][0] = i;
}

for (int j = 0; j <= len2; j++) {
    dp[0][j] = j;
}

（5）考虑输出

• 输出：dp[len1][len2] 符合语义，即 word1[0…len) 转换成 word2[0…len2) 的最小操作数

（6）空间优化：

• 根据状态转移方程，当前要填写的单元格的数值，完全取决于它的左边一格、上边一格，左上边主对角线上一个的数值。如下图：

• 因此，有两种经典的空间优化方案：① 滚动数组；② 把主对角线上要参考的数值使用一个新变量记录下来，然后在一维表格上循环赋值。由于空间问题不是这道题的瓶颈，可以不做这样的空间优化。

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        for (int i = 0; i <= m; ++i) dp[i][0] = i;
        for (int i = 0; i <= n; ++i) dp[0][i] = i;
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (word1[i - 1] == word2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
                }
            }
        }
        return dp[m][n];
    }
};

• 怎么填表
• 关于动画

类似题目

题目	思路
leetcode：72. 编辑距离 Edit Distance
leetcode：1143. 最长公共子序列 Longest Increasing Subsequence	只关心str1[0…i]，str2[0…j]，对于它们的最长公共子序列长度是多少（样本对应模型，往往以考虑结尾来组织可能性）
leetcode：583. 使得两个字符相同的最少删除次数 Delete Operation for Two Strings
leetcode：712. 使得两个字符相同时所需删除字符最小ASCII值和 Minimum ASCII Delete Sum for Two Strings