Python BFS和DFS算法

Python BFS和DFS算法

看了b站灯神的视频，整理如下。最后再加上几条实战题。
1.BFS
bfs全称是广度优先搜索，任选一个点作为起始点，然后选择和其直接相连的（按顺序展开）走下去。主要用队列实现，直接上图。两个搜索算法都只需要把图全都遍历下来就好。

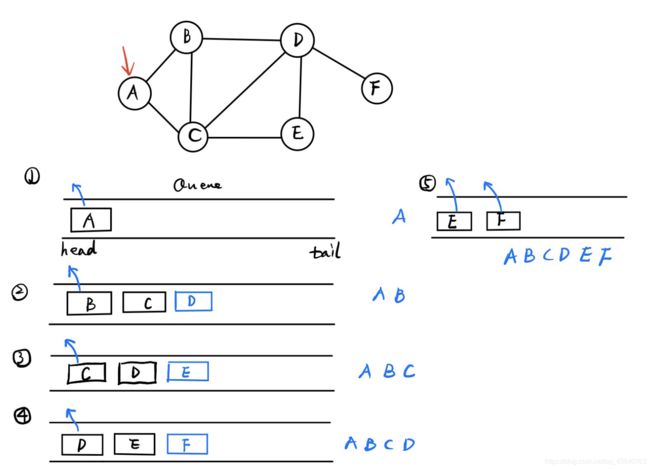
具体实现时：用字典来表示图；队列直接用python里的列表就好
python代码：

graph={
    "A":["B","C"],
    "B":["A","C","D"],
    "C":["A","B","D","E"],
    "D":["B","C","E","F"],
    "E":["C","D"],
    "F":["D"]
}

def BFS(graph,s):  #s是起始点
    queue=[]  #数组可以动态的添加或者删除 append、pop
    queue.append(s)
    seen=[]  #来保存放过的节点
    seen.append(s)
    while(len(queue)>0):
        vertex=queue.pop(0)
        nodes=graph[vertex]
        for node in nodes:
            if node not in seen:
                queue.append(node)
                seen.append(node)
        print(vertex) #把当前拿出去的节点打印出来


BFS(graph,"A")

运行结果：

下面是对BFS的一些扩展：
BFS可以求从某一点出发到其他所有点的所有路径。通过做一个映射表（字典的数据结构），在遍历的过程中，记录下上一个点的位置，其实就一句代码； parent[node]=vertex

def BFS(graph,s):  #s是起始点
    queue=[]  #数组可以动态的添加或者删除 append、pop
    queue.append(s)
    seen=[]  #来保存放过的节点
    seen.append(s)
    parent={s:None}#字典
    
    while(len(queue)>0):
        vertex=queue.pop(0)
        nodes=graph[vertex]
        for node in nodes:
            if node not in seen:
                queue.append(node)
                seen.append(node)
                parent[node]=vertex
        print(vertex) #把当前拿出去的节点打印出来
    return parent


parent=BFS(graph,"A")
print(parent)
v="E"
while v!=None:      #输出最短路径
    print(v)
    v=parent[v]

2.DFS
dfs全称是深度优先搜索，任选一个点作为起始点，然后一条路走到底，知道无路可走再往回走。用栈实现，代码和BFS基本相同，只要把BFS中的队列改为栈就好，pop(0)改为pop(),pop()代表移除最后一个元素。

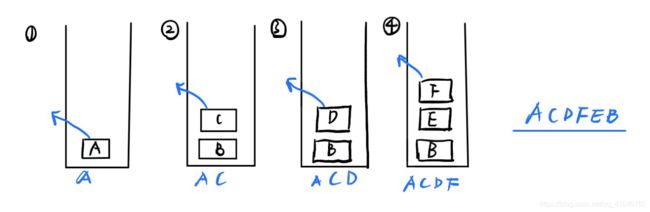
def DFS(graph,s):  #s是起始点
    stack=[]  #数组可以动态的添加或者删除 append、pop
    stack.append(s)
    seen=[]  #来保存放过的节点
    seen.append(s)
    while(len(stack)>0):
        vertex=stack.pop()  # 弹出最后一个元素
        nodes=graph[vertex]
        for node in nodes:
            if node not in seen:
                stack.append(node)
                seen.append(node)
        print(vertex) #把当前拿出去的节点打印出来

DFS(graph,"A")

运行结果为：

题目

我们沿着图中的星号线剪开，得到两个部分，每个部分的数字和都是60。
本题的要求就是请你编程判定：对给定的m x n 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。
如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割，则输出 0。
输入格式
程序先读入两个整数 m n 用空格分割 (m,n<10)。
表示表格的宽度和高度。
接下来是n行，每行m个正整数，用空格分开。每个整数不大于10000。
输出格式
输出一个整数，表示在所有解中，包含左上角的分割区可能包含的最小的格子数目。

样例输入1
3 3
10 1 52
20 30 1
1 2 3
样例输出1
3

思路参考：https://www.jianshu.com/p/0249950a9d97
先计算所有格子之和，除以2就是limit值，遍历的时候大于limit就不用继续遍历下去了，需要回溯；等于的时候记录此时遍历的格子数量，如果小于记录的最小count，那么更新；如果小于limit，那么继续遍历。
从最左上角的格子开始，进行深度优先遍历（dfs），利用递归可以很容易的做到。

m,n=map(int,input().split())
lst=[]
for i in range(n):  #输入m*n个数，变为m*n的二维矩阵
    lst.append(list(map(int,input().split())))  

visited=[[0 for i in range(m)]for j in range(n)]  #建立一个m*n 零矩阵
all_sum=0

for i in range(n):
    all_sum+=sum(lst[i])   
limit=int(all_sum/2)

move=[[0,-1],[1,0],[0,1],[-1,0]]  #设置上下左右的移动，上右下左

def judge_border(lst,x,y):   #判断有没有超出格子的边界
    if(x<0 or x>=len(lst)):
        return False
    if(y<0 or y>=len(lst[0])):
        return False
    return True

left=0    #从左上角开始，现在的总和
count=0
min_count=0
def dfs(lst,x,y,visited): #visited是上面那个 零矩阵
    global move          #全局变量？这边还没看为什么要设定全局变量
    global left
    global limit
    global count
    global min_count
    left+=lst[x][y]
    visited[x][y]=1
    count+=1

    if(left<limit):
        for i in range(4):
            if(judge_border(lst,x+move[i][0],y+move[i][1])): #没有超过边界范围的话就上下左右遍历 
                if(visited[x+move[i][0]][y+move[i][1]]==0):#这个条件是判断有没有便利过
                    dfs(lst,x+move[i][0],y+move[i][1],visited)#递归
    if(left==limit): #如果相等的话，记录此时遍历的格子数量，如果小于记录的最小count，那么更新
        if(min_count==0 or count<min_count):
            min_count=count

    visited[x][y]=0   #回溯
    count-=1
    left-=lst[x][y]

dfs(lst,0,0,visited)
print(min_count)