一文懂熵Entropy

        本文翻译自https://naokishibuya.medium.com/demystifying-entropy-f2c3221e2550

        我们常常听到【熵增】，【熵减】等概念。那么熵是什么？

        熵这个概念，最初有很多词描述它，如无序、不确定性、意外程度、不可预测、信息量等等，让很多人感到困惑。如果你对熵这个词也感到困惑，那么请继续读下去，本文将为你揭开熵的神秘面纱。

一、熵的由来

        熵最早是由鲁道夫.克劳修斯（Rudolf Clausius）提出，并应用在热力学中。熵的改变等于系统输入的热量相对于温度的改变率。

        在信息传输过程中，一直需要一种高效的、无损的信息编码方法。于是在1948年，克劳德.香农（Claude Shannon）在他的论文《通信的数学理论》中提出了信息熵的概念。并定义熵为：无损编码消息的最小平均编码长度。所以熵有三个约束条件，1）是无损编码，没有原始信息的丢失；2）平均编码长度越小越高效；3）解码端能无损地恢复原始信息。

二、高效和无损的编码

        假设我们要在两个城市Tokyo、New York传递天气信息。如果按如下的方式进行，发送一句话“Today, Tokyo's weather is fine.”。

        在发送方和接收方都明确是发送今天Tokyo天气信息的情况下，上面这句话里的冗余信息“Today”，“Tokyo's”，“Weather is”不需要发送。只需要发送天气的描述“Fine”或者“Not Fine”，就像面对面聊天，双方是知道聊得是什么主体的。

        再进一步，我们用“0”表示“Fine”，“1”表示“Not Fine”，按如下的方式编码和发送消息，可以看到这种方式是最高效和无损的编码方式。

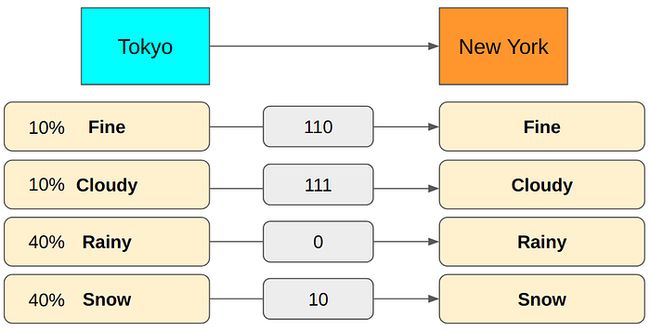
        那么“Not Fine”具体化为三种状态“Cloudy”、“Rainy”、“Snow”时，此时四种状态“Fine”、“Cloudy”、“Rainy”、“Snow”如何编码呢？如下是一种方式。

        这种编码方式有一个好处，可以通过第一位来判定是否是“Fine”，当收到消息的第一个是“0”时，即可判定是“Fine”，否则第一个是“1”时，即可判定是“Not Fine”的状态。当然，也可以有其他的编码方式，如“00”、“01”、“10”、“11”。而Fine-“0”、Cloudy-“01”、Rainy-“10”、雪-“11”这种编码就不符合，因为当接受方收到“010”表示的是“晴转雨”，还是“多云转晴”，没法区分清楚。

三、平均编码长度

        上一节提到了，发送天气消息可以有多种编码方式，那么如何衡量哪种编码方式是高效的呢。首先从累积的数据中，计算出各种天气情况的概率分布，如下图所示。

        此时的平均编码字符长度为：

        可以看到，平均编码字符长度取决于两个方面：1）概率分布，即每一种天气出现的概率值；2）编码的方式，即每一种天气使用的字符长度。如果换成如下的概率分布。

        此时，平均编码字符长度为：

        可以看到如果编码方式不变，概率分布变了后，平均编码字符长度变大了很多。（2.7bits>1.42bits）

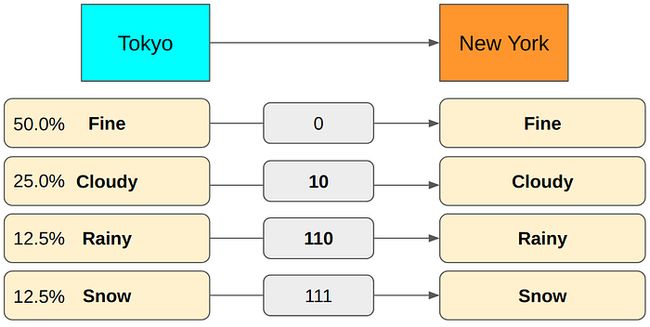
        在这种概率分布下，换成如下的编码方式。

        此时，平均编码字符长度为：

        这样的编码方式，平均编码字符长度就下降了很多，从2.7下降到了1.8。

四、最小平均编码长度

        第三部分知道了怎么计算平均编码长度，那么怎么得到最小的平均编码长度呢？假设各种天气的概率分布是已知的，现在找最小无损编码方式。

        假设给“Rainy”天气编码“0”，为了不产生混淆，其他的天气至少都要用2个字符及以上。

        计算这种方式的平均编码长度，可以知道不是最优的。遵循“给最可能发生的天气更短的编码”的原则，给“Rainy”天气编码2个字符，如下方式。

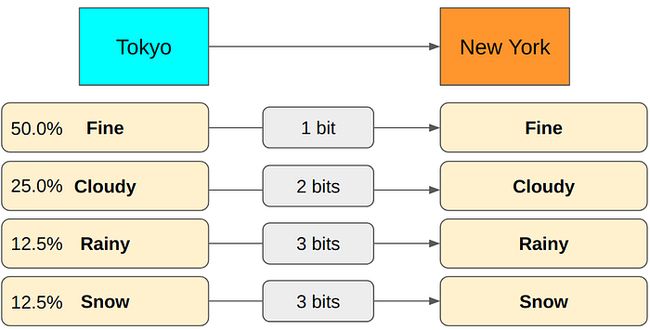
        计算这种方式的平均编码长度，可以知道也不是最优的。再次遵循“给最可能发生的天气更短的编码”的原则，给“Rainy”天气编码3个字符，如下方式。

        此时，没有必要给“Rainy”天气编码更长的字符了。理论上，这种编码方式的平均编码长度是最优的。这种通过不停更换天气编码长度的方式得到最小平均编码长度，显然是没办法用于复杂情况的。这就需要熵的计算表达式了。

五、熵的计算

        假设有8种天气状态，每种天气状态出现的概率都相等，为

        1个字符可以编码2个状态（0或者1）。增加一个字符可以编码的状态扩大一倍（2*2=4），再增加一个字符再扩大一倍后就可以编码8种状态（2*2*2），所以可以用3个字符来编码（000, 001, 010, 011, 100, 101, 110, 111）。

        减少任一个天气状态的编码长度，就会导致混淆。如把“A”状态编码为“0”，此时收到“0001010”，到底是“AAAFA”，还是“ABC”。当然，8种状态没必要用4个字符来编码。

        总之对于N种状态，需要的编码字符数为

        由于概率P=1/N，上边的表达式也可以写成

        综合以上所有信息，就可以得到熵的计算表达式如下

        P(i)为第i种状态的概率值。再举上面的天气例子看下熵的具体计算过程。

        所以，熵为

六、后记

        我们现在回头再看“无序、不确定性、意外程度、不可预测、信息量”这些同类表述词。如果熵大了，表明概率分散和状态种类多样。新的一个信息到达时，很可能是与前一个信息不一样的。即无序、不确定、不可预测。

        当一个小概率状态出现时，就有了“意外性”，能消除更多的其余状态。如前面的例子当中，当发送“Rainy”状态时，就消除了87.5%的状态分布。

        如果熵很大，平均编码长度就会很大。这就意味着每一种状态都有更多的信息。

        而熵很小，则意味着能收到更可预测的信息。

        所以，我们常常听到“企业要往【熵减】的方向发展”，因为这就意味着企业要往有序的、更少不确定性的、更少意外的、更多可预测性的、更少个体信息需要管理的方向发展了。

        但是，现代企业也要防止一直熵减，最后僵化了。

       

参考

https://naokishibuya.medium.com/demystifying-entropy-f2c3221e2550

https://zhuanlan.zhihu.com/p/149186719