比较器、二叉树、红黑树 - Java高级特性 8
目录
比较器问题的引出
Comparable比较器
Comparator比较器
二叉树
二叉树结构
二叉树的基础实现
二叉树数据删除
红黑树
数据插入平衡的修复
数据删除平衡修复
比较器指的就是就是进行大小关系的确定判断,下面分析一下比较器存在的意义。
比较器问题的引出
如果要进行数组操作,最好是使用java.util.Arrays的操作类完成,这个类里面提供有绝大部分的数组的操作支持,同时在这个类还提供有一种对象数组的排序支持:public static void sort(Object[] a)
范例:实现对象数组的排序
package cn.ren.demo;
import java.util.Arrays;
public class JavaAPIDemo {
public static void main(String[] args) throws Exception {
Integer data [] = new Integer[] {10, 9, 5, 2 ,20 } ; // 对象数组
Arrays.sort(data); // 进行对象数组的一个排序
System.out.println(Arrays.toString(data));
}
}
同样给定的是一个String型的对象数组,那么也是可以进行排序处理的。
范例:进行String对象数组排序
package cn.ren.demo;
import java.util.Arrays;
public class JavaAPIDemo {
public static void main(String[] args) throws Exception {
String data [] = new String [] {"X", "B", "A", "E", "G" } ; // 对象数组
Arrays.sort(data); // 进行对象数组的一个排序
System.out.println(Arrays.toString(data));
}
}
java.lang.Integer与java.lang.String两个类都是由系统提供的程序类,那么如果说现在有一个自定义的类需要实现排序处理。
范例:采用自定义类型进行排序处理
package cn.ren.demo;
import java.util.Arrays;
public class JavaAPIDemo {
public static void main(String[] args) throws Exception {
Person per [] = new Person [] {
new Person("perA", 18) ,
new Person("perB", 32) ,
new Person("perC", 56)
} ; //
Arrays.sort(per); // 进行对象数组的一个排序
System.out.println(Arrays.toString(per));
}
}
class Person {
private String name ;
private int age ;
public Person(String name, int age) {
this.name = name ;
this.age = age ;
}
// setter getter略
@Override
public String toString() {
return "【Person类对象】" + "姓名" + this.name + "、年龄:" + this.age + "\n" ;
}
}运行时异常:
任意的一个类在默认情况下是无法使用系统内部的类进行数组排序的 或 比较需求。是因为没有明确指定出该如何进行比较的定义(没有比较规则),那么这个时候在Java里面为了统一比较规则的定义,所以提供由比较器的接口:Comparable
Comparable比较器
通过分析可以发现如果要实现对象的比较,需要比较器来制定比较规则,而比较规则通过Comparable类实现。对于Comparable而言,需要清楚其基本的定义结构。
public interface Comparable {
/**
* 实现对象的比较处理操作
* @param o 比较对象
* @return 当前数据比传入的对象小返回负数,等于返回0
*/
public int compareTo(T o) ;
} 范例:实现自定义对象数组操作
package cn.ren.demo;
import java.util.Arrays;
public class JavaAPIDemo {
public static void main(String[] args) throws Exception {
Person per [] = new Person [] {
new Person("perA", 18) ,
new Person("perB", 32) ,
new Person("perC", 56)
} ; //
Arrays.sort(per); // 进行对象数组的一个排序
System.out.println(Arrays.toString(per));
}
}
class Person implements Comparable {
private String name ;
private int age ;
public Person(String name, int age) {
this.name = name ;
this.age = age ;
}
@Override
public int compareTo(Person per) {
return this.age - per.age ;
}
// setter getter略
@Override
public String toString() {
return "【Person类对象】" + "姓名" + this.name + "、年龄:" + this.age + "\n" ;
}
} 排序里面只需要有一个comparaTo()方法进行排序规则的定义,而后整个java系统里面就可以为其实现排序处理了。
Comparator比较器
Comparator属于一种挽救比较器的功能,其主要的目的解决一些没有使用Comparable排序的类的对象数组排序操作。
范例:现在程序项目已经开发完成了,并且由于先期的设计并没有去考虑到所谓的比较功能
class Person {
private String name ;
private int age ;
public Person(String name, int age) {
this.name = name ;
this.age = age ;
}
// setter getter略
@Override
public String toString() {
return "【Person类对象】" + "姓名" + this.name + "、年龄:" + this.age + "\n" ;
}
}
后来经过若干版本的迭代更新之后需要对Person类进行排序处理,但是又不能够去修改Person类(无法实现Comparable接口),所以这个时候就需要采用一种挽救的形式进行比较,在Arrays里面排序由另一种实现形式:
-
基于Comparator的排序处理:public static
void sort(T[] a, Comparator c)
在java.util.Comparator里面最初只定义一个排序的compare()方法:public int compare(T o1, T o2),但是后来持续发展,又出现血多的static方法。
范例:定义排序规则类
class PersonComparator implements Comparator {
@Override
public int compare(Person p1, Person p2) {
return p1.getAge() - p2.getAge() ;
}
} 在测试类进行排序处理的时候,就可以利用排序规则实现操作。
范例:排序
public class JavaAPIDemo {
public static void main(String[] args) throws Exception {
Person per [] = new Person [] {
new Person("perA", 18) ,
new Person("perB", 32) ,
new Person("perC", 56)
} ; //
Arrays.sort(per, new PersonComparator()); // 进行对象数组的一个排序
System.out.println(Arrays.toString(per));
}
}对于这种排序的操作,如果不是必须的情况下,强烈不建议使用Comparator,最好以Comparable为主。
面试题:请解释Comparable与Comparator的区别?
- java.lang.Comparable是在类定义的时候实现的父接口,主要用于定义排序的规则,里面只有一个ComparaTo()方法;
- java.util.Comparator是挽救的比较器操作,需要单独设计比较器规则类实现排序,里面有Compare()方法
二叉树
二叉树结构
在进行链表结构开发过程中会发现所有的数据按照首尾相连的状态保存,那么当要进行某一个数据查询的时候,例如:判断数据是否存在,那么这种情况下它所面对的时间复杂度为O(n),如果现在数据量小(不超过30个)情况下,那么性能上不会有太大的差别的,而一旦保存的数据量很大,这个时候时间复杂度就无法容忍。那么现在对于数据的存储结构就必须发生改变,应该尽可能的减少检索次数为出发点设计,对于现在的数据结构而言,最好的性能就是“O(logn)”,所以现在要想实现它就可以利用树的结构完成。
如果要想实现一颗树结构的定义,那么就需要去考虑数据的存储形式,在二叉树的实现之中,其基本原理如下:取第一个数据为保存的根节点,当比根节点小于等于根节点的数据放在根节点的左子树,反之放在右子树。
如果要进行数据检索的话,此时需要进行每个节点的判断,但是不会对所有的进行判断,而是区分左右的,那么它的时间复杂度O(logn)。而对于二叉树而言进行数据获取的时候有三种形式:前序(根左右)、中序(左根右)、后序遍历(左右根)。现在以中序遍历遍历的时候,最终输出:10、20、25、30、38、50、80、100。即中序遍历之后,从小到大排序。
二叉树的基础实现
在实现二叉树的处理之中,最为关键性的问题在于数据的保存,而数据由于牵扯到对象比较的问题,一定要有比较器的支持,而这个比较器首选一定是Comparable,所以本次将保存Person类数据:
class Person implements Comparable {
private String name ;
private int age ;
public Person(String name, int age) {
this.name = name ;
this.age = age ;
}
@Override
public int compareTo(Person per) {
return this.age - per.age ;
}
// setter getter略
@Override
public String toString() {
return "【Person类对象】" + "姓名" + this.name + "、年龄:" + this.age + "\n" ;
}
} 随后如果要想进行数据的保存,那么首选一定需要一个节点类。节点类里面由于牵扯到一个数据保存的问题,所以必须使用Comparable。
package cn.ren.demo;
import java.util.Arrays;
public class JavaAPIDemo {
public static void main(String[] args) throws Exception {
BinaryTree tree = new BinaryTree() ;
tree.add(new Person("小强-80",80));
tree.add(new Person("小强-30",30));
tree.add(new Person("小强-50",50));
tree.add(new Person("小强-60",60));
tree.add(new Person("小强-90",90));
System.out.println(Arrays.deepToString(tree.toArray()));
}
}
/**
* 实现二叉树的数据操作
* @author ren
*
* @param 要进行二叉树的实现
*/
class BinaryTree> { // T是使用Comparable作为泛型 ,这里定义了T的继承关系
private class Node {
private Comparable data ; // 存放Comparable,可以比较大小,同时可以强制向下转型获取数据
private Node parent ; // 保存父节点
private Node left ; // 保存左子树
private Node right ; //保存右子树
public Node(Comparable data) { // 构造方法直接进行数据的存储
this.data = data ;
}
/**
* 实现节点数据的适当位置的存储
* @param newNode 创建的新节点
*/
public void addNode(Node newNode) {
if ( newNode.data.compareTo((T)this.data) <= 0) { //比当前的节点数据小,放在左子树
if (this.left == null) { //左子树为空,可以放在左子树
this.left = newNode ;
newNode.parent = this ; // 保存父节点的指向
} else { // 需要向左边继续判断
this.left.addNode(newNode); // 继续向下判断
}
} else { // 比根节点数据大
if (this.right == null) {
this.right = newNode ;
newNode.parent = this ;
} else {
this.right.addNode(newNode);
}
}
}
/**
* 实现所有数据的获取处理,按照中序遍历的形式完成
*/
public void toArrayNode() {
if (this.left != null) { // 有左子树 ***** 左 *****
this.left.toArrayNode(); //递归调用
}
BinaryTree.this.returnData[BinaryTree.this.foot ++ ] = this.data ; // *** 根 ****
if (this.right != null) {
this.right.toArrayNode(); // *** 右 ***
}
}
}
// --------------- 以下为二叉树的功能实现 ---------------
private Node root ; // 保存根节点
private int count ; // 保存数据个数
private Object [] returnData ; // 返回数据
private int foot = 0 ; // 脚标控制
/**
* 进行数据保存
* @param data 要保存的数据内容
* @exception NullPointerException 保存数据为null时抛出的异常
*/
public void add(Comparable data) {
if (data == null) {
throw new NullPointerException("保存的数据不允许为空!") ;
}
// 所有的数据本身不具备右节点关系的匹配,那么一定要将其包装在Node类之中
Node newNode = new Node(data) ; // 保存节点
if (this.root == null) { // 现在没有根节点,则将第一节点作为根节点
this.root = newNode ;
} else { // 需要为其保存到一个合适的位置
this.root.addNode(newNode) ; // 交由Node类操作
}
this.count ++ ;
}
/**
* 以对象数组的形式返回全部数据,如果没有数据返回空
* @return 全部数据
*/
public Object[] toArray() {
if (this.count == 0) { // 没有数据
return null ;
}
this.returnData = new Object[this.count] ;
this.foot = 0 ; // 脚标清零
this.root.toArrayNode() ; // 直接通过Node类负责
return this.returnData ;
}
}
class Person implements Comparable {
private String name ;
private int age ;
public Person(String name, int age) {
this.name = name ;
this.age = age ;
}
@Override
public int compareTo(Person per) {
return this.age - per.age ;
}
// setter getter略
@Override
public String toString() {
return "【Person类对象】" + "姓名" + this.name + "、年龄:" + this.age + "\n" ;
}
} 在进行数据添加的时候,只是实现了节点关系的保存,而这种关系的保存后的结果都是有序排列。
二叉树数据删除
二叉树中的数据删除操作是非常复杂的,因为在进行数据删除的时候需要考虑的情况是比较多的:
1、如果删除的节点没有子节点,那么直接删除就行;
2、 如果待删除的节点只有子一个子节点,那么直接删除,用其子节点去替代它;这个时候考虑两种情况(都一样)
情况一:只有左子树
情况二:只有右子树
情况三:如果待删除的节点有两个子节点,将其“右的左”放在删除处
下面通过具体的代码实现删除操作功能:
范例:在Node类中追加有新的处理功能
/**
* 获取要删除的节点对象
* @param data 比较的对象
* @return 要删除的节点对象,对象一定存在
*/
public Node getRemoveNode(Comparable data) {
if(data.compareTo((T) this.data)==0) {
return this ;
} else if (data.compareTo((T) this.data) < 0) {
if (this.left != null) {
return this.left.getRemoveNode(data) ;
} else {
return null;
}
} else {
if (this.right != null) {
return this.right.getRemoveNode(data) ;
} else {
return null ;
}
}
} 范例:查找节点
外部类:
public boolean contains(Comparable data) {
if (this.count == 0) {
return false;
}
return this.root.containsNode(data);
} 内部类:
/**
* 判断是否包含某节点的数据
*
* @param data 需要判断的数据
* @return true为包含该数据,false。。
*/
public boolean containsNode(Comparable data) {
if (data.compareTo((T) this.data) == 0) {
return true;
} else if (data.compareTo((T) this.data) < 0) {
if (this.left != null) {
return this.left.containsNode(data);
} else {
return false;
}
} else {
if (this.right != null) {
return this.right.containsNode(data);
} else {
return false;
}
}
} 范例:删除数据操作,画图容易理解
有几个关键点:
- 每次都需要判断是不是根节点
- 需要判断被删除节点是父节点的左子节点还是右子节点
- 注意被删除节点,要考虑到被删除节点的右节点没有左子节点的情况,并将其和有的情况起义考虑
- 删除后,节点数量减1
/**
* 执行数据的删除处理
* @param data 需要删除的数据
*/
public void remove(Comparable data) {
if(this.count == 0){//根节点不存在
return;
}
Node removeNode = this.root.getRemoveNode(data); // 找要删除的节点
if (removeNode == null) { // 没找到
return;
}
// 找到
this.count --;
Node removeParentNode = removeNode.parent ;
boolean isRoot = (removeParentNode == null) ; // 没有父节点,为子节点
Boolean isLeftNode = null;
if(isRoot == false){ // 不是根节点时,找到删除的节点时父节点的左子点,还是右子节点
isLeftNode = data.compareTo((T)removeParentNode.data) < 0 ; // 当前节点比父节点小,则当前节点是父节点的左子结点
}
//找到要删除的节点信息了
if ( removeNode.left == null && removeNode.right == null ) { // 第一种: 无子节点
if(isRoot){
this.root=null;
}else{
//不包含子节点
removeNode.parent = null;//父节点断开引用
if(isLeftNode){
removeParentNode.left=null;
}else{
removeParentNode.right=null;
}
}
} else if (removeNode.left != null && removeNode.right == null) { // 第二种: 情况一,有左子树、没有右子树
//节点上移
if(isRoot){
this.root = this.root.left;
}else{ // 改变节点指向
if(isLeftNode){ // 子节点指向
removeParentNode.left=removeNode.left;
}else{
removeParentNode.right=removeNode.left;
}
removeNode.left.parent = removeNode.parent; // 指向父节点的指向
}
} else if (removeNode.left == null && removeNode.right != null) { // 第二种: 情况二,有右子树、没有左子树
// 节点上移
if(isRoot){
this.root = this.root.right;
}else{ // 改变节点指向
if(isLeftNode){
removeParentNode.left = removeNode.right;
}else{
removeParentNode.right = removeNode.right;
}
}
removeNode.right.parent = removeNode.parent;
} else { //有左子树和右子树,将右边节点中最左边的节点找到,改变其指向 这里不仅要改变removeNode的指向,还要改变moveNo的指向
Node moveNode = removeNode.right;//移动的节点
if(moveNode.left != null){ // 有左子节点
while (moveNode.left != null){
//还有左边的节点,一直向左找
moveNode = moveNode.left;
}
//当前moveNode就是有节点的最小左节点,当前节点只有两种情况,有右节点,或者没有,不可能有左子节点
if(moveNode.right != null){ //有右节点,右节点将替换其原始的位置
moveNode.parent.left = moveNode.right;
}else{ // 没有右节点
moveNode.parent.left = null;
}
moveNode.right = removeNode.right ;
}
// 改变原始的有节点的左右子节点指向
// 下面包含moveNode没有左子节点的情况,因此要把左节点的放在有左子点的里面,这两种情况共有的判断放在下面
moveNode.left = removeNode.left ;
// 改变父节点指向
if(isRoot){ // 如果替换的节点为根节点
this.root = moveNode ; // 改了过后它有父节点
this.root.parent = null ; // 父节点置空
}else{
moveNode.parent = removeNode.parent;
if(isLeftNode){
removeParentNode.left = moveNode;
}else{
removeParentNode.right = moveNode;
}
}
}
} 下面给出全部代码:
package cn.ren.demo;
import java.util.Arrays;
public class JavaAPIDemo {
public static void main(String[] args) throws Exception {
BinaryTree tree = new BinaryTree();
tree.add(new Person("小强-80", 80));
tree.add(new Person("小强-50", 50));
tree.add(new Person("小强-60", 60));
tree.add(new Person("小强-30", 30));
tree.add(new Person("小强-90", 90));
tree.add(new Person("小强-10", 10));
tree.add(new Person("小强-55", 55));
tree.add(new Person("小强-70", 70));
tree.add(new Person("小强-85", 85));
tree.add(new Person("小强-95", 95));
tree.remove(new Person("小强-30", 30));
System.out.println(Arrays.deepToString(tree.toArray()));
}
}
/**
* 实现二叉树的数据操作
*
* @author ren
*
* @param 要进行二叉树的实现
*/
class BinaryTree> { // T是使用Comparable作为泛型 ,这里定义了T的继承关系
private class Node {
private Comparable data; // 存放Comparable,可以比较大小,同时可以强制向下转型获取数据
private Node parent; // 保存父节点
private Node left; // 保存左子树
private Node right; // 保存右子树
public Node(Comparable data) { // 构造方法直接进行数据的存储
this.data = data;
}
/**
* 实现节点数据的适当位置的存储
*
* @param newNode 创建的新节点
*/
public void addNode(Node newNode) {
if (newNode.data.compareTo((T) this.data) <= 0) { // 比当前的节点数据小,放在左子树
if (this.left == null) { // 左子树为空,可以放在左子树
this.left = newNode;
newNode.parent = this; // 保存父节点的指向
} else { // 需要向左边继续判断
this.left.addNode(newNode); // 继续向下判断
}
} else { // 比根节点数据大
if (this.right == null) {
this.right = newNode;
newNode.parent = this;
} else {
this.right.addNode(newNode);
}
}
}
/**
* 实现所有数据的获取处理,按照中序遍历的形式完成
*/
public void toArrayNode() {
if (this.left != null) { // 有左子树 ***** 左 *****
this.left.toArrayNode(); // 递归调用
}
BinaryTree.this.returnData[BinaryTree.this.foot++] = this.data; // *** 根 ****
if (this.right != null) {
this.right.toArrayNode(); // *** 右 ***
}
}
/**
* 判断是否包含某节点的数据
*
* @param data 需要判断的数据
* @return true为包含该数据,false。。
*/
public boolean containsNode(Comparable data) {
if (data.compareTo((T) this.data) == 0) {
return true;
} else if (data.compareTo((T) this.data) < 0) {
if (this.left != null) {
return this.left.containsNode(data);
} else {
return false;
}
} else {
if (this.right != null) {
return this.right.containsNode(data);
} else {
return false;
}
}
}
/**
* 获取要删除的节点对象
*
* @param data 比较的对象
* @return 要删除的节点对象,对象一定存在
*/
public Node getRemoveNode(Comparable data) {
if (data.compareTo((T) this.data) == 0) {
return this;
} else if (data.compareTo((T) this.data) < 0) {
if (this.left != null) {
return this.left.getRemoveNode(data);
} else {
return null;
}
} else {
if (this.right != null) {
return this.right.getRemoveNode(data);
} else {
return null;
}
}
}
}
// --------------- 以下为二叉树的功能实现 ---------------
private Node root; // 保存根节点
private int count; // 保存数据个数
private Object[] returnData; // 返回数据
private int foot = 0; // 脚标控制
/**
* 进行数据保存
*
* @param data 要保存的数据内容
* @exception NullPointerException 保存数据为null时抛出的异常
*/
public void add(Comparable data) {
if (data == null) {
throw new NullPointerException("保存的数据不允许为空!");
}
// 所有的数据本身不具备右节点关系的匹配,那么一定要将其包装在Node类之中
Node newNode = new Node(data); // 保存节点
if (this.root == null) { // 现在没有根节点,则将第一节点作为根节点
this.root = newNode;
} else { // 需要为其保存到一个合适的位置
this.root.addNode(newNode); // 交由Node类操作
}
this.count++;
}
public boolean contains(Comparable data) {
if (this.count == 0) {
return false;
}
return this.root.containsNode(data);
}
/**
* 以对象数组的形式返回全部数据,如果没有数据返回空
*
* @return 全部数据
*/
public Object[] toArray() {
if (this.count == 0) { // 没有数据
return null;
}
this.returnData = new Object[this.count];
this.foot = 0; // 脚标清零
this.root.toArrayNode(); // 直接通过Node类负责
return this.returnData;
}
/**
* 执行数据的删除处理
* @param data 需要删除的数据
*/
public void remove(Comparable data) {
if(this.count == 0){//根节点不存在
return;
}
Node removeNode = this.root.getRemoveNode(data); // 找要删除的节点
if (removeNode == null) { // 没找到
return;
}
// 找到
this.count --;
Node removeParentNode = removeNode.parent ;
boolean isRoot = (removeParentNode == null) ; // 没有父节点,为子节点
Boolean isLeftNode = null;
if(isRoot == false){ // 不是根节点时,找到删除的节点时父节点的左子点,还是右子节点
isLeftNode = data.compareTo((T)removeParentNode.data) < 0 ; // 当前节点比父节点小,则当前节点是父节点的左子结点
}
//找到要删除的节点信息了
if ( removeNode.left == null && removeNode.right == null ) { // 第一种: 无子节点
if(isRoot){
this.root=null;
}else{
//不包含子节点
removeNode.parent = null;//父节点断开引用
if(isLeftNode){
removeParentNode.left=null;
}else{
removeParentNode.right=null;
}
}
} else if (removeNode.left != null && removeNode.right == null) { // 第二种: 情况一,有左子树、没有右子树
//节点上移
if(isRoot){
this.root = this.root.left;
}else{ // 改变节点指向
if(isLeftNode){ // 子节点指向
removeParentNode.left=removeNode.left;
}else{
removeParentNode.right=removeNode.left;
}
removeNode.left.parent = removeNode.parent; // 指向父节点的指向
}
} else if (removeNode.left == null && removeNode.right != null) { // 第二种: 情况二,有右子树、没有左子树
// 节点上移
if(isRoot){
this.root = this.root.right;
}else{ // 改变节点指向
if(isLeftNode){
removeParentNode.left = removeNode.right;
}else{
removeParentNode.right = removeNode.right;
}
}
removeNode.right.parent = removeNode.parent;
} else { //有左子树和右子树,将右边节点中最左边的节点找到,改变其指向 这里不仅要改变removeNode的指向,还要改变moveNo的指向
Node moveNode = removeNode.right;//移动的节点
if(moveNode.left != null){ // 有左子节点
while (moveNode.left != null){
//还有左边的节点,一直向左找
moveNode = moveNode.left;
}
//当前moveNode就是有节点的最小左节点,当前节点只有两种情况,有右节点,或者没有,不可能有左子节点
if(moveNode.right != null){ //有右节点,右节点将替换其原始的位置
moveNode.parent.left = moveNode.right;
}else{ // 没有右节点
moveNode.parent.left = null;
}
moveNode.right = removeNode.right ;
}
// 改变原始的有节点的左右子节点指向
// 下面包含moveNode没有左子节点的情况,因此要把左节点的放在有左子点的里面,这两种情况共有的判断放在下面
moveNode.left = removeNode.left ;
// 改变父节点指向
if(isRoot){ // 如果替换的节点为根节点
this.root = moveNode ; // 改了过后它有父节点
this.root.parent = null ; // 父节点置空
}else{
moveNode.parent = removeNode.parent;
if(isLeftNode){
removeParentNode.left = moveNode;
}else{
removeParentNode.right = moveNode;
}
}
}
}
}
class Person implements Comparable {
private String name;
private int age;
public Person(String name, int age) {
this.name = name;
this.age = age;
}
@Override
public int compareTo(Person per) {
return this.age - per.age;
}
// setter getter略
@Override
public String toString() {
return "【Person类对象】" + "姓名" + this.name + "、年龄:" + this.age + "\n";
}
}
红黑树
通过整个二叉树的实现已经清楚二叉树的特点:数据查询的时候可以提供更好的性能。但是这样树的结构有一定缺陷,比如只有一个分支树,它这样就与链表无区别了,所以提出平衡的概念。
如果要想达到良好效果的二叉树,首先应该是一个平衡二叉树,所有的节点的层次深度相同,如下:
如果数据按照以上的形式保存,那么二叉树的检索操作执行效率一定是最高的。关键点在于如果在增删操作里面保持平衡。于是提出了红黑树的概念,红黑树本质上是二叉查找树,它在二叉查找树的基础上添加了一个颜色标记,同时具有一定规则,这些规则使红黑树保持平衡。从1.8开始大量运用红黑树。结构如下:
enum Color {
RED, BLACK ;
}
class BinaryTree {
private class Node {
private T data ;
private Node parent ;
private Node left ;
private Node right ;
private Color color ;
}
}
对于Node的颜色标记也可以使用true或false来实现,即不一定使用枚举。一个标准的红黑树的结构如下:
红黑树特点(面试关键):
-
每个节点要么是红色,要么是黑色;
-
根节点必须是黑色;
-
每个叶子节点是黑色
-
如果一个节点是红色的那么它的子节点必须是黑色的。
-
任意一结点到每个叶子结点的路径都包含数量相同的黑结点。
红黑树并不是一个完美平衡二叉查找树,红黑树这种平衡为黑色完美平衡。java中实现的红黑树将使用null来代表空节点,因此遍历红黑树时看不到叶子节点,反而看到叶子节点是红色的。
利用红色节点和黑色节点实现均衡的控制,简单理解红黑树的结构,就是为了进行左旋和右旋的控制,以保持树的平衡性。
但是对于平衡性需要考虑两种情况:数据增加的平衡、数据删除的平衡。即增加和删除都需要对树进行平衡修复的。
红黑树能自平衡靠三种操作:左旋、右旋和变色。
- 左旋:以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。
- 右旋:以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。
- 变色:结点的颜色由红变黑或由黑变红。
![]()
![]()
数据插入平衡的修复
在进行红黑树处理的时候,为了方便新节点都会以红色标记。在数据插入有几种情况及其修复方法如下:
-
原树为空,插入则需将根节点涂黑。根据特点2。
-
原树不为空,插入时按照插入的父节点颜色,分为两种情况:
1. 其父节点为黑色,直接插入。
2. 其父节点为红色,根据父节点和其叔叔节点的颜色,分为两种情况: 注:插入结点总是存在祖父结点。
1)叔叔节点为红色
2)叔叔节点为黑色,根据插入节点位置,分为两种情况:
(1)插入节点是父节点的左子节点,没有叔叔节点也是这样
(2)插入节点是父节点的右子节点
2 中 1)做法:
我们把50结点设为红色了,如果50的父结点是黑色,那么无需再做任何处理;但如果50的父结点是红色,根据特点4,此时红黑树已不平衡了,所以还需要把50当作新的插入结点,继续做插入操作自平衡处理,直到平衡为止。
试想下50刚好为根结点时,那么根据特点2,我们必须把50重新设为黑色,那么树的红黑结构变为:黑黑红。换句话说,从根结点到叶子结点的路径中,黑色结点增加了。这也是唯一一种会增加红黑树黑色结点层数的插入情景。显然红黑树的生长是自底向上的。
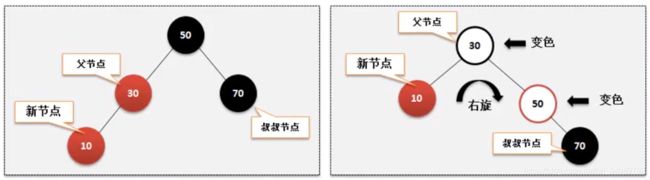
2 中 1)中 (1)做法:将30、50变色,然后右旋处理。
2 中 1)中 (2)做法:先左旋,变成上面的情况( 2 中 1)中 (1)的做法 )
下面进行完整分析一次:以2 中 1)中 (1)情况为例:
上图违反特点4
上图出现红红连接
在红黑树进行修复的过程中,它需要根据当前节点和当前节点的父节点和叔叔节点之间的颜色来推断是否进行修复处理。变化只存在在新节点父节点和叔叔节点之间。新节点只有在插入到根结点才会变色。
下面将https://www.jianshu.com/p/e136ec79235c中的内容复制过来,作为标准。
插入操作包括两部分工作:一查找插入的位置;二插入后自平衡。查找插入的父结点很简单,跟查找操作区别不大:
- 从根结点开始查找;
- 若根结点为空,那么插入结点作为根结点,结束。
- 若根结点不为空,那么把根结点作为当前结点;
- 若当前结点为null,返回当前结点的父结点,结束。
- 若当前结点key等于查找key,那么该key所在结点就是插入结点,更新结点的值,结束。
- 若当前结点key大于查找key,把当前结点的左子结点设置为当前结点,重复步骤4;
- 若当前结点key小于查找key,把当前结点的右子结点设置为当前结点,重复步骤4;
如图6所示。
![]()
图6 红黑树插入位置查找
ok,插入位置已经找到,把插入结点放到正确的位置就可以啦,但插入结点是应该是什么颜色呢?答案是红色。理由很简单,红色在父结点(如果存在)为黑色结点时,红黑树的黑色平衡没被破坏,不需要做自平衡操作。但如果插入结点是黑色,那么插入位置所在的子树黑色结点总是多1,必须做自平衡。
所有插入情景如图7所示。
![]()
图7 红黑树插入情景
嗯,插入情景很多呢,8种插入情景!但情景1、2和3的处理很简单,而情景4.2和情景4.3只是方向反转而已,懂得了一种情景就能推出另外一种情景,所以总体来看,并不复杂,后续我们将一个一个情景来看,把它彻底搞懂。
另外,根据二叉树的性质,除了情景2,所有插入操作都是在叶子结点进行的。这点应该不难理解,因为查找插入位置时,我们就是在找子结点为空的父结点的。
在开始每个情景的讲解前,我们还是先来约定下,如图8所示。
![]()
图8 插入操作结点的叫法约定
图8的字母并不代表结点Key的大小。I表示插入结点,P表示插入结点的父结点,S表示插入结点的叔叔结点,PP表示插入结点的祖父结点。
好了,下面让我们一个一个来分析每个插入的情景以其处理。
插入情景1:红黑树为空树
最简单的一种情景,直接把插入结点作为根结点就行,但注意,根据红黑树性质2:根节点是黑色。还需要把插入结点设为黑色。
处理:把插入结点作为根结点,并把结点设置为黑色。
插入情景2:插入结点的Key已存在
插入结点的Key已存在,既然红黑树总保持平衡,在插入前红黑树已经是平衡的,那么把插入结点设置为将要替代结点的颜色,再把结点的值更新就完成插入。
处理:
- 把I设为当前结点的颜色
- 更新当前结点的值为插入结点的值
插入情景3:插入结点的父结点为黑结点
由于插入的结点是红色的,当插入结点的黑色时,并不会影响红黑树的平衡,直接插入即可,无需做自平衡。
处理:直接插入。
插入情景4:插入结点的父结点为红结点
再次回想下红黑树的性质2:根结点是黑色。如果插入的父结点为红结点,那么该父结点不可能为根结点,所以插入结点总是存在祖父结点。这点很重要,因为后续的旋转操作肯定需要祖父结点的参与。
情景4又分为很多子情景,下面将进入重点部分,各位看官请留神了。
插入情景4.1:叔叔结点存在并且为红结点
从红黑树性质4可以,祖父结点肯定为黑结点,因为不可以同时存在两个相连的红结点。那么此时该插入子树的红黑层数的情况是:黑红红。显然最简单的处理方式是把其改为:红黑红。如图9和图10所示。
处理:
- 将P和S设置为黑色
- 将PP设置为红色
- 把PP设置为当前插入结点
![]()
图9 插入情景4.1_1
![]()
图10 插入情景4.1_2
可以看到,我们把PP结点设为红色了,如果PP的父结点是黑色,那么无需再做任何处理;但如果PP的父结点是红色,根据性质4,此时红黑树已不平衡了,所以还需要把PP当作新的插入结点,继续做插入操作自平衡处理,直到平衡为止。
试想下PP刚好为根结点时,那么根据性质2,我们必须把PP重新设为黑色,那么树的红黑结构变为:黑黑红。换句话说,从根结点到叶子结点的路径中,黑色结点增加了。这也是唯一一种会增加红黑树黑色结点层数的插入情景。
我们还可以总结出另外一个经验:红黑树的生长是自底向上的。这点不同于普通的二叉查找树,普通的二叉查找树的生长是自顶向下的。
插入情景4.2:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的左子结点
单纯从插入前来看,也即不算情景4.1自底向上处理时的情况,叔叔结点非红即为叶子结点(Nil)。因为如果叔叔结点为黑结点,而父结点为红结点,那么叔叔结点所在的子树的黑色结点就比父结点所在子树的多了,这不满足红黑树的性质5。后续情景同样如此,不再多做说明了。
前文说了,需要旋转操作时,肯定一边子树的结点多了或少了,需要租或借给另一边。插入显然是多的情况,那么把多的结点租给另一边子树就可以了。
插入情景4.2.1:插入结点是其父结点的左子结点
处理:
- 将P设为黑色
- 将PP设为红色
- 对PP进行右旋
![]()
图11 插入情景4.2.1
由图11可得,左边两个红结点,右边不存在,那么一边一个刚刚好,并且因为为红色,肯定不会破坏树的平衡。
咦,可以把P设为红色,I和PP设为黑色吗?答案是可以!看过《算法:第4版》的同学可能知道,书中讲解的就是把P设为红色,I和PP设为黑色。但把P设为红色,显然又会出现情景4.1的情况,需要自底向上处理,做多了无谓的操作,既然能自己消化就不要麻烦祖辈们啦~
插入情景4.2.2:插入结点是其父结点的右子结点
这种情景显然可以转换为情景4.2.1,如图12所示,不做过多说明了。
处理:
- 对P进行左旋
- 把P设置为插入结点,得到情景4.2.1
- 进行情景4.2.1的处理
![]()
图12 插入情景4.2.2
插入情景4.3:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的右子结点
该情景对应情景4.2,只是方向反转,不做过多说明了,直接看图。
插入情景4.3.1:插入结点是其父结点的右子结点
处理:
- 将P设为黑色
- 将PP设为红色
- 对PP进行左旋
![]()
图13 插入情景4.3.1
插入情景4.3.2:插入结点是其父结点的左子结点
处理:
- 对P进行右旋
- 把P设置为插入结点,得到情景4.3.1
- 进行情景4.3.1的处理
![]()
图14 插入情景4.3.2
好了,讲完插入的所有情景了。可能又同学会想:上面的情景举例的都是第一次插入而不包含自底向上处理的情况,那么上面所说的情景都适合自底向上的情况吗?答案是肯定的。理由很简单,但每棵子树都能自平衡,那么整棵树最终总是平衡的。好吧,在出个习题,请大家拿出笔和纸画下试试(请务必动手画下,加深印象):
习题1:请画出图15的插入自平衡处理过程。(答案见文末)
![]()
图15 习题1
数据删除平衡修复
删除部分参考:https://www.jianshu.com/p/e136ec79235c 。
二叉树删除结点找替代结点有3种情情景:
- 情景1:若删除结点无子结点,直接删除
- 情景2:若删除结点只有一个子结点,用子结点替换删除结点
- 情景3:若删除结点有两个子结点,用后继结点(大于删除结点的最小结点)替换删除结点
把二叉树所有结点投射在X轴上,所有结点都是从左到右排好序的,所有目标结点的前后结点就是对应前继和后继结点。
![]()
删除结点被替代后,在不考虑结点的键值的情况下,对于树来说,可以认为删除的是替代结点。替代节点是即将被替换到删除结点的位置的替代结点,在删除前,它还在原来所在位置参与树的子平衡,平衡后再替换到删除结点的位置,才算删除完成。
![]()
根据删除操作的替代节点来选择进行修复的方法:
-
替代节点为黑色根节点,直接删
-
根据替代节点的颜色,分为两种情况:
1. 替代节点红色,删除也了不会影响红黑树的平衡,只要把替换结点的颜色设为删除的结点的颜色即可重新平衡。
2. 替代节点为黑色,替换结点是其父结点的左子结点,根据当前节点的兄弟节点颜色,分为两种情况:
1)替代节点的兄弟节点为红色
2)兄弟节点为黑色,根据兄弟节点的子节点的颜色,分为三种情况:
(1)子节点均为黑
(2)右子节点为黑,左子节点为红
(3)右子节点为红,左子节点为红或黑
2 中 1)做法:将30的父节点涂红,30的兄弟节点涂黑,然后左旋
2 中 2)中 (1)做法:将70变色,
2 中 2)中 (2)做法:
2 中 2)中 (3)做法:注意这里70没有变色,图错
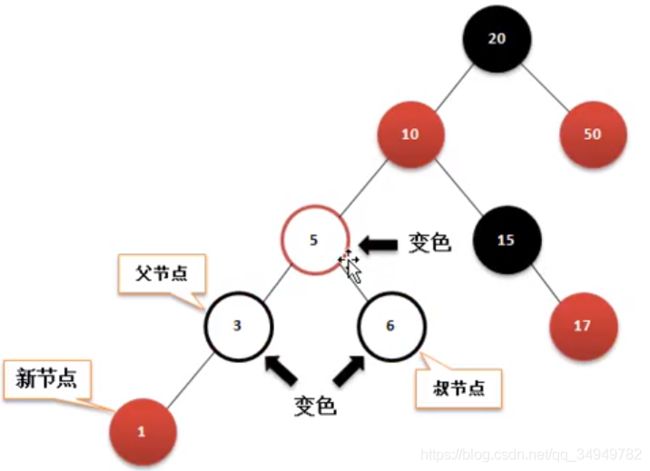
下面看一个完整例子:
删除5
删除6
在红黑树中修复的目的是为了保证树中的黑色节点的数量平衡,黑色节点的数量平衡了,才可能得到“”O(logn)“的性能,但是修复的过程是红黑的处理,另一方面是黑子节点保存的层次。
下面将https://www.jianshu.com/p/e136ec79235c中的内容复制过来,作为标准。
红黑树插入已经够复杂了,但删除更复杂,也是红黑树最复杂的操作了。但稳住,胜利的曙光就在前面了!
红黑树的删除操作也包括两部分工作:一查找目标结点;而删除后自平衡。查找目标结点显然可以复用查找操作,当不存在目标结点时,忽略本次操作;当存在目标结点时,删除后就得做自平衡处理了。删除了结点后我们还需要找结点来替代删除结点的位置,不然子树跟父辈结点断开了,除非删除结点刚好没子结点,那么就不需要替代。
二叉树删除结点找替代结点有3种情情景:
- 情景1:若删除结点无子结点,直接删除
- 情景2:若删除结点只有一个子结点,用子结点替换删除结点
- 情景3:若删除结点有两个子结点,用后继结点(大于删除结点的最小结点)替换删除结点
补充说明下,情景3的后继结点是大于删除结点的最小结点,也是删除结点的右子树种最左结点。那么可以拿前继结点(删除结点的左子树最右结点)替代吗?可以的。但习惯上大多都是拿后继结点来替代,后文的讲解也是用后继结点来替代。另外告诉大家一种找前继和后继结点的直观的方法(不知为何没人提过,大家都知道?):把二叉树所有结点投射在X轴上,所有结点都是从左到右排好序的,所有目标结点的前后结点就是对应前继和后继结点。如图16所示。
![]()
图16 二叉树投射x轴后有序
接下来,讲一个重要的思路:删除结点被替代后,在不考虑结点的键值的情况下,对于树来说,可以认为删除的是替代结点!话很苍白,我们看图17。在不看键值对的情况下,图17的红黑树最终结果是删除了Q所在位置的结点!这种思路非常重要,大大简化了后文讲解红黑树删除的情景!
![]()
图17 删除结点换位思路
基于此,上面所说的3种二叉树的删除情景可以相互转换并且最终都是转换为情景1!
- 情景2:删除结点用其唯一的子结点替换,子结点替换为删除结点后,可以认为删除的是子结点,若子结点又有两个子结点,那么相当于转换为情景3,一直自顶向下转换,总是能转换为情景1。(对于红黑树来说,根据性质5.1,只存在一个子结点的结点肯定在树末了)
- 情景3:删除结点用后继结点(肯定不存在左结点),如果后继结点有右子结点,那么相当于转换为情景2,否则转为为情景1。
二叉树删除结点情景关系图如图18所示。
![]()
图18 二叉树删除情景转换
综上所述,删除操作删除的结点可以看作删除替代结点,而替代结点最后总是在树末。有了这结论,我们讨论的删除红黑树的情景就少了很多,因为我们只考虑删除树末结点的情景了。
同样的,我们也是先来总体看下删除操作的所有情景,如图19所示。
![]()
图19 红黑树删除情景
哈哈,是的,即使简化了还是有9种情景!但跟插入操作一样,存在左右对称的情景,只是方向变了,没有本质区别。同样的,我们还是来约定下,如图20所示。
![]()
图20 删除操作结点的叫法约定
图20的字母并不代表结点Key的大小。R表示替代结点,P表示替代结点的父结点,S表示替代结点的兄弟结点,SL表示兄弟结点的左子结点,SR表示兄弟结点的右子结点。灰色结点表示它可以是红色也可以是黑色。
值得特别提醒的是,R是即将被替换到删除结点的位置的替代结点,在删除前,它还在原来所在位置参与树的子平衡,平衡后再替换到删除结点的位置,才算删除完成。
万事具备,我们进入最后的也是最难的讲解。
删除情景1:替换结点是红色结点
我们把替换结点换到了删除结点的位置时,由于替换结点时红色,删除也了不会影响红黑树的平衡,只要把替换结点的颜色设为删除的结点的颜色即可重新平衡。
处理:颜色变为删除结点的颜色
删除情景2:替换结点是黑结点
当替换结点是黑色时,我们就不得不进行自平衡处理了。我们必须还得考虑替换结点是其父结点的左子结点还是右子结点,来做不同的旋转操作,使树重新平衡。
删除情景2.1:替换结点是其父结点的左子结点
删除情景2.1.1:替换结点的兄弟结点是红结点
若兄弟结点是红结点,那么根据性质4,兄弟结点的父结点和子结点肯定为黑色,不会有其他子情景,我们按图21处理,得到删除情景2.1.2.3(后续讲解,这里先记住,此时R仍然是替代结点,它的新的兄弟结点SL和兄弟结点的子结点都是黑色)。
处理:
- 将S设为黑色
- 将P设为红色
- 对P进行左旋,得到情景2.1.2.3
- 进行情景2.1.2.3的处理
![]()
图21 删除情景2.1.1
删除情景2.1.2:替换结点的兄弟结点是黑结点
当兄弟结点为黑时,其父结点和子结点的具体颜色也无法确定(如果也不考虑自底向上的情况,子结点非红即为叶子结点Nil,Nil结点为黑结点),此时又得考虑多种子情景。
删除情景2.1.2.1:替换结点的兄弟结点的右子结点是红结点,左子结点任意颜色
即将删除的左子树的一个黑色结点,显然左子树的黑色结点少1了,然而右子树又又红色结点,那么我们直接向右子树“借”个红结点来补充黑结点就好啦,此时肯定需要用旋转处理了。如图22所示。
处理:
- 将S的颜色设为P的颜色
- 将P设为黑色
- 将SR设为黑色
- 对P进行左旋
![]()
图22 删除情景2.1.2.1
平衡后的图怎么不满足红黑树的性质?前文提醒过,R是即将替换的,它还参与树的自平衡,平衡后再替换到删除结点的位置,所以R最终可以看作是删除的。另外图2.1.2.1是考虑到第一次替换和自底向上处理的情况,如果只考虑第一次替换的情况,根据红黑树性质,SL肯定是红色或为Nil,所以最终结果树是平衡的。如果是自底向上处理的情况,同样,每棵子树都保持平衡状态,最终整棵树肯定是平衡的。后续的情景同理,不做过多说明了。
删除情景2.1.2.2:替换结点的兄弟结点的右子结点为黑结点,左子结点为红结点
兄弟结点所在的子树有红结点,我们总是可以向兄弟子树借个红结点过来,显然该情景可以转换为情景2.1.2.1。图如23所示。
处理:
- 将S设为红色
- 将SL设为黑色
- 对S进行右旋,得到情景2.1.2.1
- 进行情景2.1.2.1的处理
![]()
图23 删除情景2.1.2.2
删除情景2.1.2.3:替换结点的兄弟结点的子结点都为黑结点
好了,此次兄弟子树都没红结点“借”了,兄弟帮忙不了,找父母呗,这种情景我们把兄弟结点设为红色,再把父结点当作替代结点,自底向上处理,去找父结点的兄弟结点去“借”。但为什么需要把兄弟结点设为红色呢?显然是为了在P所在的子树中保证平衡(R即将删除,少了一个黑色结点,子树也需要少一个),后续的平衡工作交给父辈们考虑了,还是那句,当每棵子树都保持平衡时,最终整棵总是平衡的。
处理:
- 将S设为红色
- 把P作为新的替换结点
- 重新进行删除结点情景处理
![]()
图24 情景2.1.2.3
删除情景2.2:替换结点是其父结点的右子结点
好啦,右边的操作也是方向相反,不做过多说明了,相信理解了删除情景2.1后,肯定可以理解2.2。
删除情景2.2.1:替换结点的兄弟结点是红结点
处理:
- 将S设为黑色
- 将P设为红色
- 对P进行右旋,得到情景2.2.2.3
- 进行情景2.2.2.3的处理
![]()
图25 删除情景2.2.1
删除情景2.2.2:替换结点的兄弟结点是黑结点
删除情景2.2.2.1:替换结点的兄弟结点的左子结点是红结点,右子结点任意颜色
处理:
- 将S的颜色设为P的颜色
- 将P设为黑色
- 将SL设为黑色
- 对P进行右旋
![]()
图26 删除情景2.2.2.1
删除情景2.2.2.2:替换结点的兄弟结点的左子结点为黑结点,右子结点为红结点
处理:
- 将S设为红色
- 将SR设为黑色
- 对S进行左旋,得到情景2.2.2.1
- 进行情景2.2.2.1的处理
![]()
图27 删除情景2.2.2.2
删除情景2.2.2.3:替换结点的兄弟结点的子结点都为黑结点
处理:
- 将S设为红色
- 把P作为新的替换结点
- 重新进行删除结点情景处理
![]()
图28 删除情景2.2.2.3
综上,红黑树删除后自平衡的处理可以总结为:
- 自己能搞定的自消化(情景1)
- 自己不能搞定的叫兄弟帮忙(除了情景1、情景2.1.2.3和情景2.2.2.3)
- 兄弟都帮忙不了的,通过父母,找远方亲戚(情景2.1.2.3和情景2.2.2.3)
哈哈,是不是跟现实中很像,当我们有困难时,首先先自己解决,自己无力了总兄弟姐妹帮忙,如果连兄弟姐妹都帮不上,再去找远方的亲戚了。这里记忆应该会好记点~
最后再做个习题加深理解(请不熟悉的同学务必动手画下):
***习题2:请画出图29的删除自平衡处理过程。
![]()
红黑树在线生成的网站,来做各种情景梳理很有帮助:在线生成红黑树。
思考题和习题答案
思考题1:黑结点可以同时包含一个红子结点和一个黑子结点吗?
答:可以。如下图的F结点:
![]()
习题1:请画出图15的插入自平衡处理过程。
答:
![]()
习题2:请画出图29的删除自平衡处理过程。
答:
![]()
参考:https://www.jianshu.com/p/e136ec79235c,附有部分原文,防止连接失效