Leetcode题解---一维子数组
目录
1. 两数之和
39. 组合总和
40. 组合总和 II
15. 三数之和
16. 最接近的三数之和
560. 和为K的子数组
923. 三数之和的多种可能
18. 四数之和
454. 四数相加 II
494. 目标和
53. 最大子序和
从n个数中随机选出k个数,并判断和是不是素数
152. 乘积最大子数组
312. 戳气球
581. 最短无序连续子数组
1262. 可被三整除的最大和
1013. 将数组分成和相等的三个部分
698. 划分为k个相等的子集
1. 两数之和
Python代码1:
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
for i in range(len(nums)):
a = target - nums[i]
for j in range(i+1,len(nums),1):
if a == nums[j]:
return [i,j]代码2:
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
dic = {}
for k,v in enumerate(nums):
if target-v in dic:
return [k, dic[target-v]]
dic[v] = k还有一份代码,我在本地运行没有问题,带网站上提交时就显示超时,不知道为什么,有哪位大神知道求告知:
def twoSum(nums,target):
for i in range(len(nums)):
j = i + 1
while j <= len(nums)-1:
if target == nums[i] + nums[j]:
return [i, j]
break
else:
j += 139. 组合总和
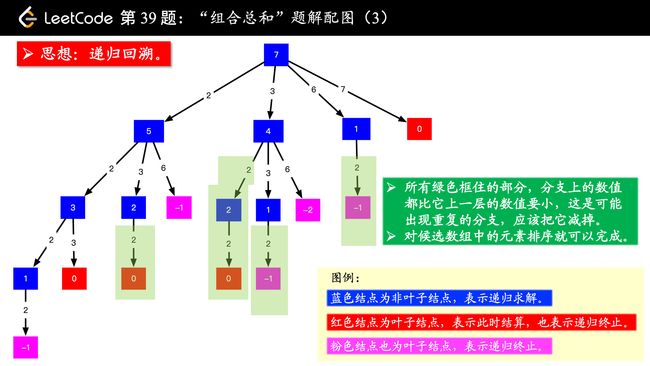
思路:根据示例 1:输入: candidates = [2,3,6,7],target = 7。
候选数组里有 2 ,如果找到了 7 - 2 = 5 的所有组合,再在之前加上 2 ,就是 7 的所有组合;
同理考虑 3,如果找到了 7 - 3 = 4 的所有组合,再在之前加上 3 ,就是 7 的所有组合,依次这样找下去;
上面的思路就可以画成下面的树形图。
其实这里思路已经介绍完了,大家可以自己尝试在纸上画一下这棵树。然后编码实现,如果遇到问题,再看下面的文字。
![]()
说明:
蓝色结点表示:尝试找到组合之和为该数的所有组合,怎么找呢?逐个减掉候选数组中的元素即可;
以 target = 7 为根结点,每一个分支做减法;
减到 00 或者负数的时候,到了叶子结点;
减到 00 的时候结算,这里 “结算” 的意思是添加到结果集;
从根结点到叶子结点(必须为 0)的路径,就是题目要我们找的一个组合。
把文字的部分去掉。
![]()
如果这样编码的话,会发现提交不能通过,这是因为递归树画的有问题,下面看一下是什么原因。
画出图以后,我看了一下,我这张图画出的结果有 44 个 00,对应的路径是 [[2, 2, 3], [2, 3, 2], [3, 2, 2], [7]],而示例中的解集只有 [[7], [2, 2, 3]],很显然,重复的原因是在较深层的结点值考虑了之前考虑过的元素,因此我们需要设置“下一轮搜索的起点”即可(这里可能没有说清楚,已经尽力了)。
去重复
在搜索的时候,需要设置搜索起点的下标 begin ,由于一个数可以使用多次,下一层的结点从这个搜索起点开始搜索;
在搜索起点 begin 之前的数因为以前的分支搜索过了,所以一定会产生重复。
剪枝提速
如果一个数位搜索起点都不能搜索到结果,那么比它还大的数肯定搜索不到结果,基于这个想法,我们可以对输入数组进行排序,以减少搜索的分支;
排序是为了提高搜索速度,非必要;
搜索问题一般复杂度较高,能剪枝就尽量需要剪枝。把候选数组排个序,遇到一个较大的数,如果以这个数为起点都搜索不到结果,后面的数就更搜索不到结果了。
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
size = len(candidates)
if size == 0:
return []
# 剪枝是为了提速,在本题非必需
candidates.sort()
# 在遍历的过程中记录路径,它是一个栈
path = []
res = []
# 注意要传入 size ,在 range 中, size 取不到
self.__dfs(candidates, 0, size, path, res, target)
return res
def __dfs(self, candidates, begin, size, path, res, target):
# 先写递归终止的情况
if target == 0:
# Python 中可变对象是引用传递,因此需要将当前 path 里的值拷贝出来
# 或者使用 path.copy()
res.append(path[:])
return
for index in range(begin, size):
residue = target - candidates[index]
# “剪枝”操作,不必递归到下一层,并且后面的分支也不必执行
if residue < 0:
break
path.append(candidates[index])
# 因为下一层不能比上一层还小,起始索引还从 index 开始
self.__dfs(candidates, index, size, path, res, residue)
path.pop()
if __name__ == '__main__':
candidates = [2, 3, 6, 7]
target = 7
solution = Solution()
result = solution.combinationSum(candidates, target)
print(result)// author:rmokerone
#include
#include
using namespace std;
class Solution {
private:
vector candidates;
vector> res;
vector path;
public:
void DFS(int start, int target) {
if (target == 0) {
res.push_back(path);
return;
}
for (int i = start;
i < candidates.size() && target - candidates[i] >= 0; i++) {
path.push_back(candidates[i]);
DFS(i, target - candidates[i]);
path.pop_back();
}
}
vector> combinationSum(vector &candidates, int target) {
std::sort(candidates.begin(), candidates.end());
this->candidates = candidates;
DFS(0, target);
return res;
}
}; 40. 组合总和 II
//Python
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
def dfs(begin, path, residue):
if residue == 0:
res.append(path[:])
return
for index in range(begin, size):
if candidates[index] > residue:
break
if index > begin and candidates[index - 1] == candidates[index]:
continue
path.append(candidates[index])
dfs(index + 1, path, residue - candidates[index])
path.pop()
size = len(candidates)
if size == 0:
return []
candidates.sort()
res = []
dfs(0, [], target)
return res//C++
class Solution {
private:
vector candidates;
vector> res;
vector path;
public:
void DFS(int start, int target) {
if (target == 0) {
res.push_back(path);
return;
}
for (int i = start; i < candidates.size() && target - candidates[i] >= 0; i++) {
if (i > start && candidates[i] == candidates[i - 1])
continue;
path.push_back(candidates[i]);
// 元素不可重复利用,使用下一个即i+1
DFS(i + 1, target - candidates[i]);
path.pop_back();
}
}
vector> combinationSum2(vector &candidates, int target) {
sort(candidates.begin(), candidates.end());
this->candidates = candidates;
DFS(0, target);
return res;
}
};
参考代码 2:以 0 为根结点,依次加上数组中的数字,直到大于 target 或者等于 target,把等于 target 的结果记录到结果集中。
#include
#include
#include 15. 三数之和
排序 + 双指针
题目中要求找到所有「不重复」且和为 00 的三元组,这个「不重复」的要求使得我们无法简单地使用三重循环枚举所有的三元组。这是因为在最坏的情况下,数组中的元素全部为 00,即
[0, 0, 0, 0, 0, ..., 0, 0, 0]
任意一个三元组的和都为 00。如果我们直接使用三重循环枚举三元组,会得到 O(N^3)O(N
3
) 个满足题目要求的三元组(其中 NN 是数组的长度)时间复杂度至少为 O(N^3)O(N
3
)。在这之后,我们还需要使用哈希表进行去重操作,得到不包含重复三元组的最终答案,又消耗了大量的空间。这个做法的时间复杂度和空间复杂度都很高,因此我们要换一种思路来考虑这个问题。
「不重复」的本质是什么?我们保持三重循环的大框架不变,只需要保证:
第二重循环枚举到的元素不小于当前第一重循环枚举到的元素;
第三重循环枚举到的元素不小于当前第二重循环枚举到的元素。
也就是说,我们枚举的三元组 (a, b, c)(a,b,c) 满足 a \leq b \leq ca≤b≤c,保证了只有 (a, b, c)(a,b,c) 这个顺序会被枚举到,而 (b, a, c)(b,a,c)、(c, b, a)(c,b,a) 等等这些不会,这样就减少了重复。要实现这一点,我们可以将数组中的元素从小到大进行排序,随后使用普通的三重循环就可以满足上面的要求。
同时,对于每一重循环而言,相邻两次枚举的元素不能相同,否则也会造成重复。举个例子,如果排完序的数组为
[0, 1, 2, 2, 2, 3]
^ ^ ^
我们使用三重循环枚举到的第一个三元组为 (0, 1, 2)(0,1,2),如果第三重循环继续枚举下一个元素,那么仍然是三元组 (0, 1, 2)(0,1,2),产生了重复。因此我们需要将第三重循环「跳到」下一个不相同的元素,即数组中的最后一个元素 33,枚举三元组 (0, 1, 3)(0,1,3)。
下面给出了改进的方法的伪代码实现:
nums.sort()
for first = 0 .. n-1
// 只有和上一次枚举的元素不相同,我们才会进行枚举
if first == 0 or nums[first] != nums[first-1] then
for second = first+1 .. n-1
if second == first+1 or nums[second] != nums[second-1] then
for third = second+1 .. n-1
if third == second+1 or nums[third] != nums[third-1] then
// 判断是否有 a+b+c==0
check(first, second, third)
这种方法的时间复杂度仍然为 O(N^3)O(N
3
),毕竟我们还是没有跳出三重循环的大框架。然而它是很容易继续优化的,可以发现,如果我们固定了前两重循环枚举到的元素 aa 和 bb,那么只有唯一的 cc 满足 a+b+c=0a+b+c=0。当第二重循环往后枚举一个元素 b'b
′
时,由于 b' > bb
′
>b,那么满足 a+b'+c'=0a+b
′
+c
′
=0 的 c'c
′
一定有 c' < cc
′
在数组中一定出现在 cc 的左侧。也就是说,我们可以从小到大枚举 bb,同时从大到小枚举 cc,即第二重循环和第三重循环实际上是并列的关系。
有了这样的发现,我们就可以保持第二重循环不变,而将第三重循环变成一个从数组最右端开始向左移动的指针,从而得到下面的伪代码:
nums.sort()
for first = 0 .. n-1
if first == 0 or nums[first] != nums[first-1] then
// 第三重循环对应的指针
third = n-1
for second = first+1 .. n-1
if second == first+1 or nums[second] != nums[second-1] then
// 向左移动指针,直到 a+b+c 不大于 0
while nums[first]+nums[second]+nums[third] > 0
third = third-1
// 判断是否有 a+b+c==0
check(first, second, third)
这个方法就是我们常说的「双指针」,当我们需要枚举数组中的两个元素时,如果我们发现随着第一个元素的递增,第二个元素是递减的,那么就可以使用双指针的方法,将枚举的时间复杂度从 O(N^2)O(N
2
) 减少至 O(N)O(N)。为什么是 O(N)O(N) 呢?这是因为在枚举的过程每一步中,「左指针」会向右移动一个位置(也就是题目中的 bb),而「右指针」会向左移动若干个位置,这个与数组的元素有关,但我们知道它一共会移动的位置数为 O(N)O(N),均摊下来,每次也向左移动一个位置,因此时间复杂度为 O(N)O(N)。
注意到我们的伪代码中还有第一重循环,时间复杂度为 O(N)O(N),因此枚举的总时间复杂度为 O(N^2)O(N
2
)。由于排序的时间复杂度为 O(N \log N)O(NlogN),在渐进意义下小于前者,因此算法的总时间复杂度为 O(N^2)O(N
2
)。
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
nums.sort()
ans = list()
# 枚举 a
for first in range(n):
# 需要和上一次枚举的数不相同
if first > 0 and nums[first] == nums[first - 1]:
continue
# c 对应的指针初始指向数组的最右端
third = n - 1
target = -nums[first]
# 枚举 b
for second in range(first + 1, n):
# 需要和上一次枚举的数不相同
if second > first + 1 and nums[second] == nums[second - 1]:
continue
# 需要保证 b 的指针在 c 的指针的左侧
while second < third and nums[second] + nums[third] > target:
third -= 1
# 如果指针重合,随着 b 后续的增加
# 就不会有满足 a+b+c=0 并且 b16. 最接近的三数之和
解题思路和求三数之和类似
- 首先对nums排序
- 固定当前
i, 从[i+1, n)中寻找j、k - 中间有两个小优化
class Solution:
def threeSumClosest(self, nums: List[int], target: int) -> int:
if not nums: return 0
if len(nums) < 3: return sum(nums)
ans = float('inf')
nums.sort()
for i in range(len(nums)):
# 优化点 1
if i > 0 and nums[i] == nums[i-1]: continue
# 新的 t
t = target - nums[i]
j, k = i + 1, len(nums) - 1
while j < k:
# 优化点 2
if t == nums[j] + nums[k]: return target
# 当前 j、k更接近target
if abs(t - nums[j] - nums[k]) < abs(target - ans):
ans = nums[i] + nums[j] + nums[k]
# 移动j | k
if t > nums[j] + nums[k]:
j += 1
else:
k -= 1
return ans
560. 和为K的子数组
hashmap 来简化时间复杂度:
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
d = {}
acc = count = 0
for num in nums:
acc += num
if acc == k:
count += 1
if acc - k in d:
count += d[acc-k]
if acc in d:
d[acc] += 1
else:
d[acc] = 1
return count第二个想法是前缀和,保存一个数组的前缀和,然后利用差分法得出任意区间段的和,这种想法是可行的,代码如下:
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
cnt, n = 0, len(nums)
pre = [0] * (n + 1)
for i in range(1, n + 1):
pre[i] = pre[i - 1] + nums[i - 1]
for i in range(1, n + 1):
for j in range(i, n + 1):
if (pre[j] - pre[i - 1] == k): cnt += 1
return cnt
923. 三数之和的多种可能
三指针代码:
class Solution(object):
def threeSumMulti(self, A, target):
MOD = 10**9 + 7
ans = 0
A.sort()
for i, x in enumerate(A):
# We'll try to find the number of i < j < k
# with A[j] + A[k] == T, where T = target - A[i].
# The below is a "two sum with multiplicity".
T = target - A[i]
j, k = i+1, len(A) - 1
while j < k:
# These steps proceed as in a typical two-sum.
if A[j] + A[k] < T:
j += 1
elif A[j] + A[k] > T:
k -= 1
# These steps differ:
elif A[j] != A[k]: # We have A[j] + A[k] == T.
# Let's count "left": the number of A[j] == A[j+1] == A[j+2] == ...
# And similarly for "right".
left = right = 1
while j + 1 < k and A[j] == A[j+1]:
left += 1
j += 1
while k - 1 > j and A[k] == A[k-1]:
right += 1
k -= 1
# We contributed left * right many pairs.
ans += left * right
ans %= MOD
j += 1
k -= 1
else:
# M = k - j + 1
# We contributed M * (M-1) / 2 pairs.
ans += (k-j+1) * (k-j) / 2
ans %= MOD
break
return ans18. 四数之和
思路同三数之和:
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
if not nums or len(nums) < 4:
return []
nums.sort()
res = []
for a in range(len(nums)-3):
if a > 0 and nums[a] == nums[a-1]:
continue
for b in range(a+1,len(nums)-2):
if b > a+1 and nums[b] == nums[b-1]:
continue
c = b+1
d = len(nums)-1
while c < d:
sum = nums[a]+nums[b]+nums[c]+nums[d]
if sum == target:
res.append([nums[a],nums[b],nums[c],nums[d]])
while c454. 四数相加 II
初始化计数器 dic,dic 记录数组 A 和 B 元素的和,及其次数
遍历数组 C 和 D,累加满足四数相加和为 0 的个数
class Solution:
def fourSumCount(self, A: List[int], B: List[int], C: List[int], D: List[int]) -> int:
dic = collections.Counter()
ans = 0
for a in A:
for b in B:
dic[a+b] += 1
for c in C:
for d in D:
ans += dic[-c-d]
return ans
494. 目标和
class Solution:
def findTargetSumWays(self, nums: List[int], S: int) -> int:
"""
(1)思路:动态规划
我们用 dp[i][j] 表示用数组中的前 i 个元素,组成和为 j 的方案数。考虑第 i 个数 nums[i],它可以被添
加 + 或 - ,那么从dp[i-1][m] —> dp[i][j] 可以在 dp[i-1][m]的基础上加上 nums[i] 或者减去 nums[i],
因此状态转移方程如下:
dp[i][j] = dp[i-1][j-nums[i]] + dp[i-1][j + nums[i]]
(2)复杂度:
- 时间复杂度:O(N * sums) 其中 N 是数组 nums 的长度
- 空间复杂度:O(N * sums)
"""
import collections
# 获取数组长度和数组和的最大值
array_length, max_sum = len(nums), sum(nums)
# 定义和初始化dp数组
# 因为该数组所能组成的值的区间为[min_sum, max_sum],即一共有 max_sum - min_sum + 1 种值
# 但是为了方便,可以直接定义为dict的形式,这样就可以一直增加key而不需要去计算dp数组第二维的长度,同时不用管下标为
# 负数的情况,直接将下标转化为dict中的key
# 这样不存在的key,也会默认是0
dp = [collections.defaultdict(int) for _ in range(len(nums))]
# 之所以dp[0][-nums[0]] 使用 += 1 而不是直接赋值1,是为了处理nums[0]就等于0的情况
# 如果nums[0], 那么dp[0][0] = 2 而不是 1
dp[0][nums[0]] = 1
dp[0][-nums[0]] += 1
# 遍历nums数组,更行dp数组的值
for i in range(1, array_length):
for j in range(-max_sum, max_sum+1):
# 状态转移方程
# 当dp[i][j]不等于的0的时候,代表至少存在一种方法得到j值
dp[i][j] = dp[i - 1].get(j + nums[i], 0) + dp[i - 1].get(j - nums[i], 0)
return dp[-1][S]53. 最大子序和
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
dp=[0]*(len(nums))
dp[0]=nums[0]
for i in range(1,len(nums)):
if dp[i-1]<=0:
dp[i]=nums[i]
else:
dp[i]=dp[i-1]+nums[i]
return max(dp)从n个数中随机选出k个数,并判断和是不是素数
#include
#include
using namespace std;
int x[20],n,k;//依照题目所设
bool isprime(int n){//判断是否质数
int s=sqrt(double(n));
for(int i=2;i<=s;i++){
if(n%i==0)return false;
}
return true;
}
int rule(int choose_left_num,int already_sum,int start,int end){//choose_left_num为剩余的k,already_sum为前面累加的和,start和end为全组合剩下数字的选取范围;调用递归生成全组合,在过程中逐渐把K个数相加,当选取的数个数为0时,直接返回前面的累加和是否为质数即可
if(choose_left_num==0)return isprime(already_sum);
int sum=0;
for(int i=start;i<=end;i++){
sum+=rule(choose_left_num-1,already_sum+x[i],i+1,end);
}
return sum;
}
int main(){
cin>>n>>k;
for(int i =0;i>x[i];
cout< 152. 乘积最大子数组
动态规划:
class Solution:
def maxProduct(self, nums: List[int]) -> int:
if not nums: return
res = nums[0]
pre_max = nums[0]
pre_min = nums[0]
for num in nums[1:]:
cur_max = max(pre_max * num, pre_min * num, num)
cur_min = min(pre_max * num, pre_min * num, num)
res = max(res, cur_max)
pre_max = cur_max
pre_min = cur_min
return res312. 戳气球
class Solution:
def maxCoins(self, nums: List[int]) -> int:
#nums首尾添加1,方便处理边界情况
nums.insert(0,1)
nums.insert(len(nums),1)
store = [[0]*(len(nums)) for i in range(len(nums))]
def range_best(i,j):
m = 0
#k是(i,j)区间内最后一个被戳的气球
for k in range(i+1,j): #k取值在(i,j)开区间中
#以下都是开区间(i,k), (k,j)
left = store[i][k]
right = store[k][j]
a = left + nums[i]*nums[k]*nums[j] + right
if a > m:
m = a
store[i][j] = m
#对每一个区间长度进行循环
for n in range(2,len(nums)): #区间长度 #长度从3开始,n从2开始
#开区间长度会从3一直到len(nums)
#因为这里取的是range,所以最后一个数字是len(nums)-1
#对于每一个区间长度,循环区间开头的i
for i in range(0,len(nums)-n): #i+n = len(nums)-1
#计算这个区间的最多金币
range_best(i,i+n)
return store[0][len(nums)-1]581. 最短无序连续子数组
解题思路
1.计算排序前后的差值
2.记录第一次和最后一次非零值对应的索引
3.maxindex-minindex+1为排序的最小数组
class Solution:
def findUnsortedSubarray(self, nums: List[int]) -> int:
diff = []
for i, (unsort, sort) in enumerate(zip(nums, sorted(nums))):
if unsort != sort:
diff.append(i)
return len(diff) and diff[-1] - diff[0] + 11262. 可被三整除的最大和
动态规划:
class Solution:
def maxSumDivThree(self, nums: List[int]) -> int:
f = [0, -1, -1]
for num in nums:
g = f[:]
for i in range(3):
if f[i] != -1:
g[(i + num % 3) % 3] = max(g[(i + num % 3) % 3], f[i] + num)
f = g
return f[0]
1013. 将数组分成和相等的三个部分
双指针:设sum_A为A所有元素之和,a与b为指针分为指向首端元素和尾端元素(因为分割数组必须非空,因此a>0,b 虽然是分成三等份,但实际上只需要求出left和right的值,mid也就呼之欲出:
(1)利用双指针在首尾分别滑动,当left和right都为sum_A/3时停止(若在a<=b之前还未达到终止条件则直接返回False);
(2)根据a和b的值求出mid;
(3)对比left、mid以及right是否相等返回判断结果。class Solution:
def canThreePartsEqualSum(self, A: List[int]) -> bool:
sum_A = sum(A)
a,b = 1,len(A) - 2
left,right = A[0],A[-1]
while a < len(A)-2 and b > 1:
if left != sum_A // 3:
left += A[a]
a += 1
if right != sum_A // 3:
right += A[b]
b -= 1
if a > b:
return False
if left == right == sum_A // 3:
break
mid = sum(A[a:b+1])
return left == mid == right698. 划分为k个相等的子集
class Solution(object):
def canPartitionKSubsets(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: bool
"""
sum_nums = sum(nums)
avg = sum_nums // k
if k <= 0 or sum_nums % k != 0 or max(nums) > avg:
return False
n = len(nums)
visited = [0] * n
nums = sorted(nums, reverse=True)
return self.canPartition(nums, visited, 0, k, 0, 0, avg)
def canPartition(self, nums, visited, start_index, k, cur_sum, cur_num, target):
if k == 1:
return True
if cur_sum == target and cur_num > 0:
return self.canPartition(nums, visited, 0, k - 1, 0, 0, target)
if cur_sum > target:
return False
for i in range(start_index, len(nums)):
if visited[i] == 0:
visited[i] = 1
if self.canPartition(nums, visited, i + 1, k, cur_sum + nums[i], cur_num + 1, target):
return True
visited[i] = 0
return False