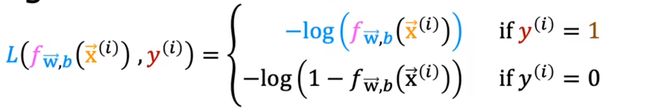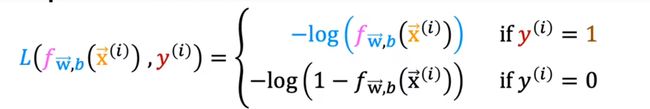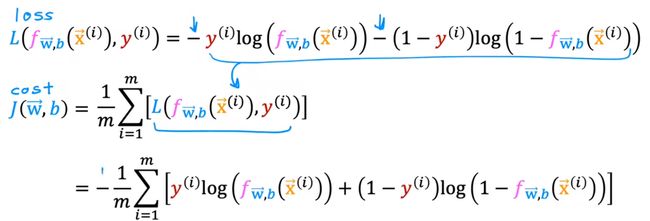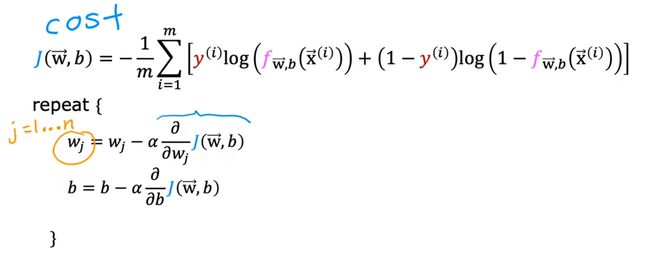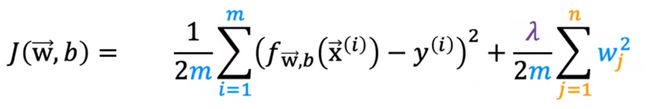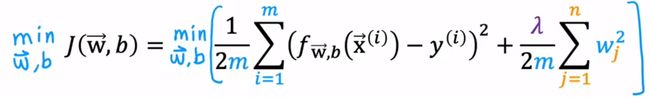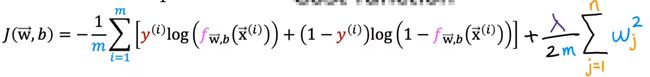第一章：part3分类模型

分类学习输出的值是从几个可能的值中选出的，但是这种方法不能继续使用线性回归，需要使用新的模型：逻辑回归

1. 二分类问题介绍

二分类模型

很多问题规定了答案：

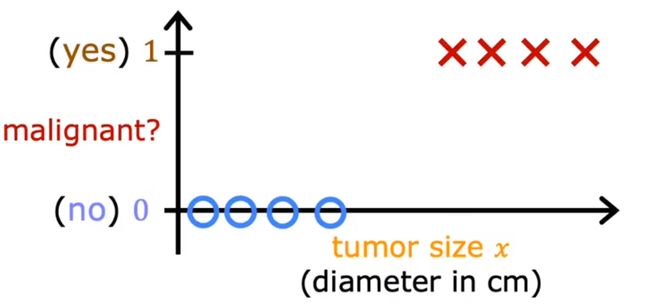
例如：下面的回答只有 yes/no（1/0）

对于上述问题，用来表示的数据集：

1：是肿瘤

0：不是肿瘤

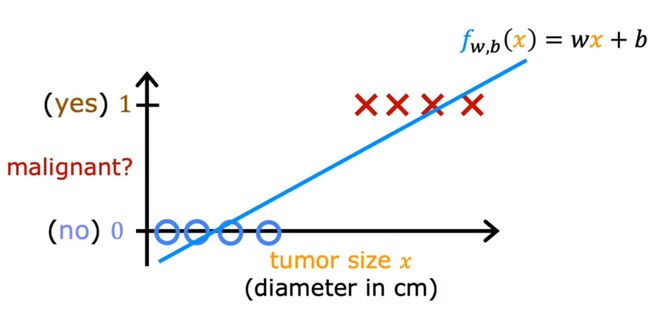
• 如果使用线性回归进行预测，很明显是不合理的

下面将讲述如何将上述数据进行处理，得到一个想要的结果

逻辑回归模型

$$f_{w,b}(x)=g((w\cdot x)+b)=\frac{1}{1+e^{-(w\cdot x)+b}}$$

由于我们的输出结果为**0（no）-1（yes）**区间内，想要得到一个函数，输出结果也为0-1：

• 逻辑函数

首先我们来看构建逻辑回归的函数

$$\begin{gathered} g(z)=1/1+e^{-z} \\ z大的时候趋近1，z小的时候趋近0 \end{gathered}$$

• 逻辑回归算法的建立

1. 将直线线性回归模型代入

线性回归模型设为z代入

2. 代入上述函数

该函数则为逻辑回归模型

这样就可以使得线性回归方程中的结果在0-1区间内

函数输出结果实例分析：

例如：
有一个病人，x为肿瘤大小，y输出为肿瘤结果的概率（0-1），则下述的例子为：有70 %的概率患病

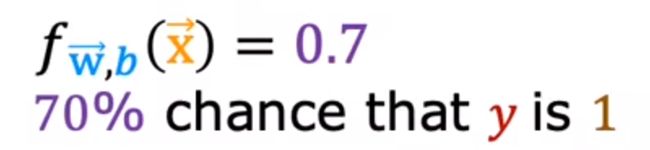
结合概率论的知识，通常情况下还可以写作：

表示在x的情况下（对应的w与b），y=1的概率

决策边界

如果我们只想要得到0/1的结果，我们可以设置阈值

例如：

$$ f(x)= \begin{cases} 0,& \text{if x >0.5} \\ 1, & \text{if x <0.5} \end{cases} $$

• 定义

在x=0.5时，意味着w*x+b=0（如下图）

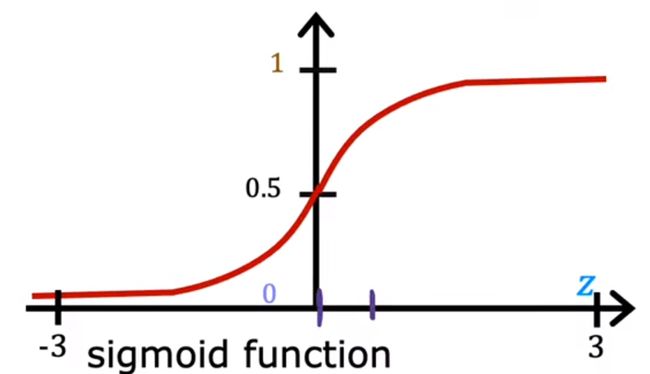
同时也意味着f(x)的值为0和1的概率相同

这样的拟合函数有什么意义呢，如下：

例：训练集如下所示，x为1，o为0，假设函数为回归函数，有两个维度，w1=1，w2=1，b=-3

决策边界可以表示为：
$$\begin{gathered} z=w\cdot x+b=0 \\ 代入w1，w2，b \\ {x}_1+x_2-3=0 \\ {x}_1+x_2=3 \end{gathered}$$

这条紫线 为决策边界

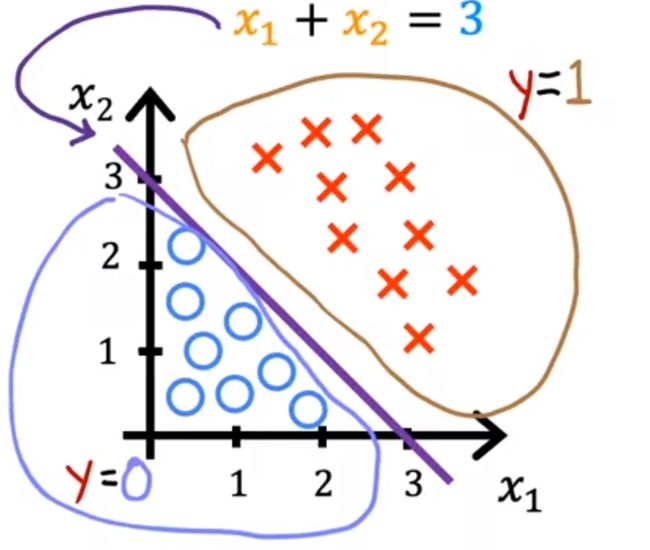
这就是回归模型的基本作用，下面我们具体来介绍如何训练回归模型

• 构建代价函数
• 实现梯度下降算法

---

2. 逻辑回归中的代价函数

逻辑回归中的代价函数实现

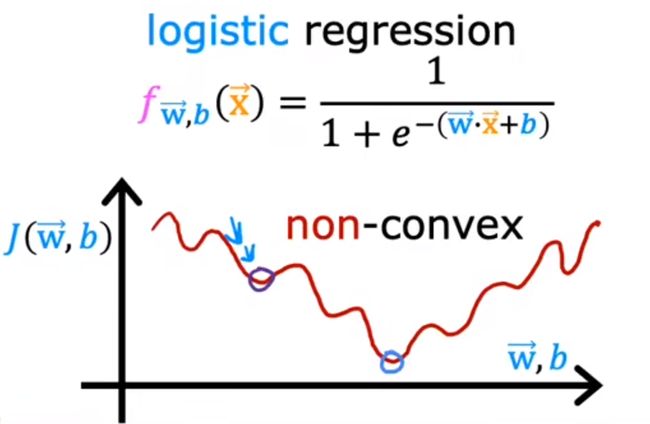
如果以之前的代价函数进行使用：
$$J(w,b)=\frac{1}{2m}\sum _{i=0}^m(f_{w,b}(x^{(i)})-y{)}^2$$

会有许多局部最小点，不方便使用

• 优化代价函数：

将1/2放在了求和函数的里面

使用这样的凸函数可以保证梯度下降算法的使用

• 损失函数L

可以告诉我们模型在样本的训练效果如何

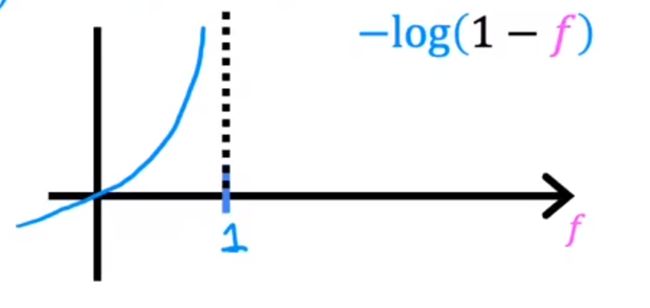
如果y的值为0，则损失函数为：

理解：

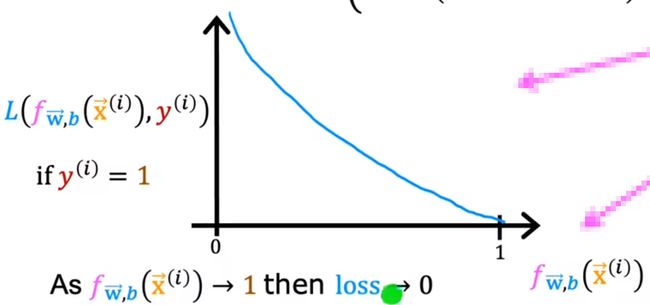
如果y的值为1，则损失函数为：

$$-log(f):0<f<1$$

即,当阈值为f(x)时，结果视为y=1，对应的损失值是多少

如果y的值为0，则损失函数为：

$$-log(1-f):0<f<1$$

即,当阈值为f(x)时，结果视为y=0，对应的损失值是多少

构建好了损失函数，那么接下来如果能知道使得J(w,b)最小的w&b，那么就可以实现逻辑回归

简化代价函数

将上述的式子可以简化为一个式子：

紧接着将上述式子代入代价函数

得到最优式
$$J(w,b)=-\frac{1}{m}\sum _{i=0}^m[y^{(i)}log(f_{w,b}(x^{(i)}))-(1-y^{(i)})log(1-f_{w,b}(x^{(i)}))]$$

这种代价函数是根据，极大似然估计推断出来的，感兴趣的可以自行了解

---

3. 实现梯度下降

通过梯度下降算法，我们可以找到使得J(w,b)最小的w&b

对上述式子的偏导分别进行计算：

代入偏导，得到下述式子：

注：此处的fw,b和线性回归的不同
$$f_{w,b}(x)=\frac{1}{1+e^{-(w\cdot x)+b}}$$

---

4. 过拟合问题

介绍过拟合（overfit）

• 术语介绍

• 泛化：模型对于未知样本的推理能力

• 欠拟合（underfit）

下面为房价的模型

对于一组数据拟合具有偏差，所以也可以称为：高偏差（high bias）

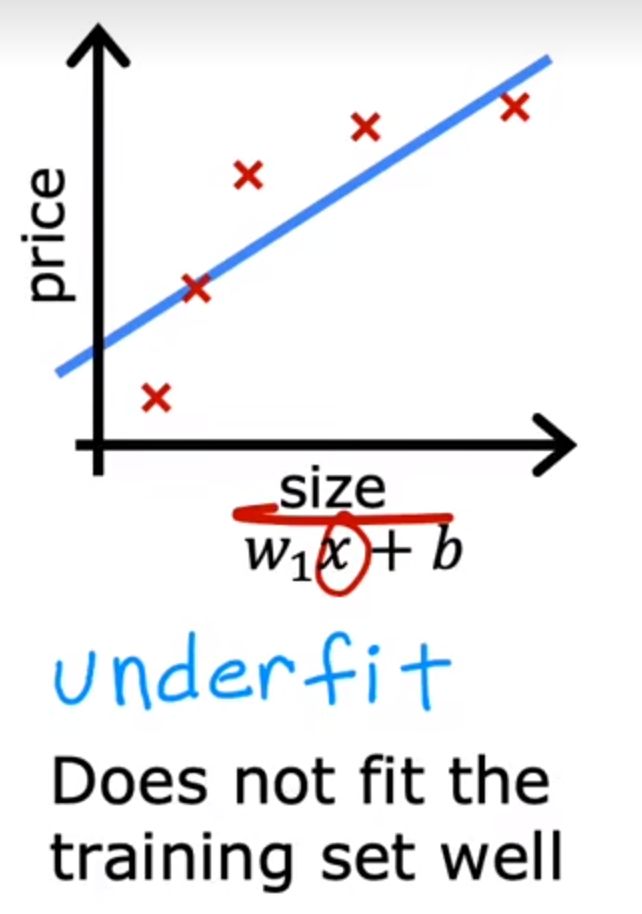
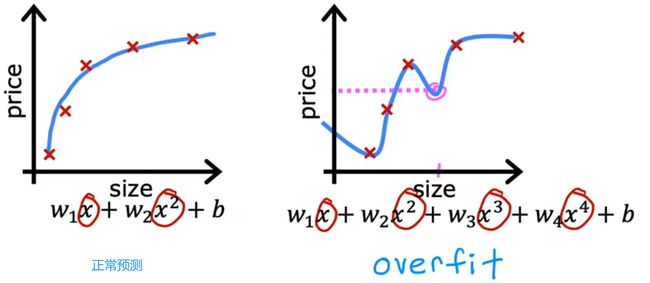
• 过拟合（overfit）

对于一组数据拟合过好失去预测能力，所以也可以称为：高方差（high variance）

所以，我们应该寻找一个既没有高偏差，也没有高方差的模型

解决过拟合问题

1. 更多的训练数据

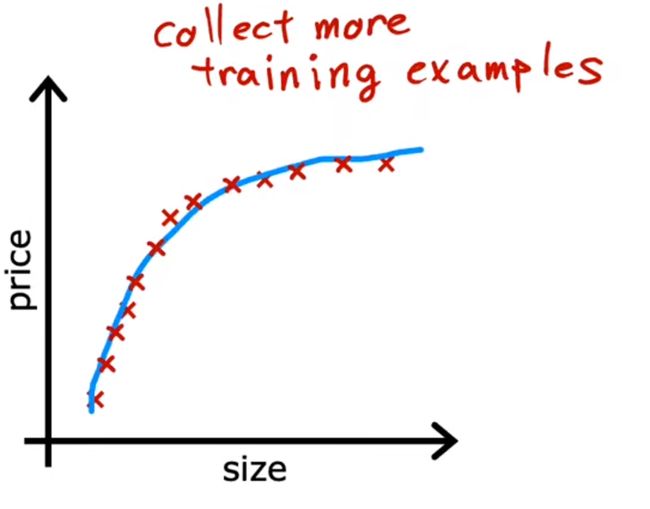
2. 观察是否可以使用更少的特征（x1、x2、x3…）

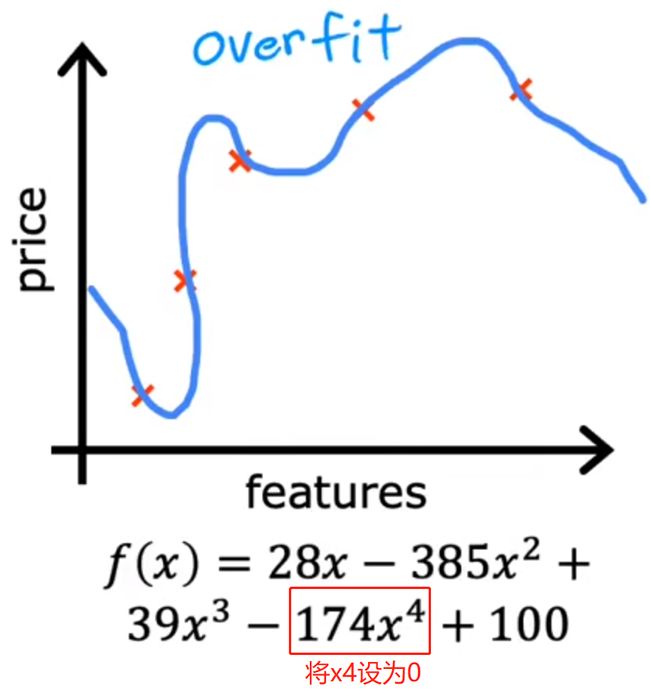
缺点：有些重要特征可能被丢弃

3. 正则化

尽可能缩小参数的值

保留所有特征，但防止特征权重过大

正则化

正则化只考虑w的影响，不考虑b（b对整体拟合影响较小）

• 原理

如果二项式的模型是正常的

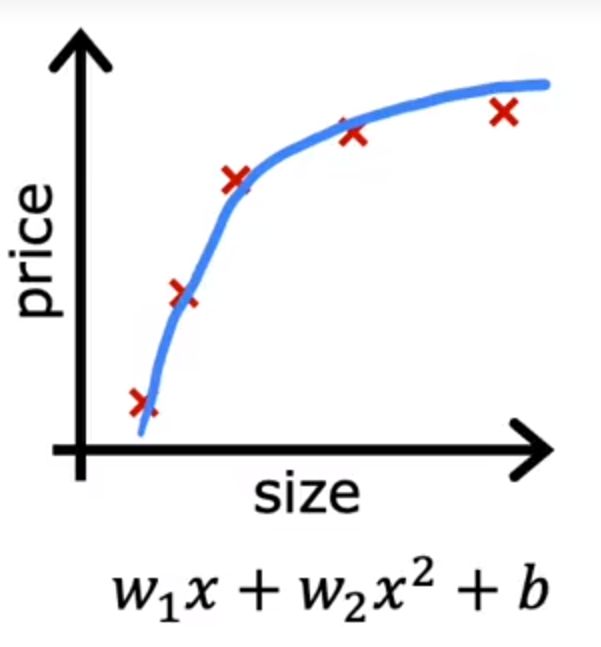
但四项式模型过拟合

我们则需要减少w3和w4的大小，防止模型过拟合

所以我们可以通过在代价函数后面增加w3和w4：

为了使代价函数最小，w3和w4肯定会赋予小值

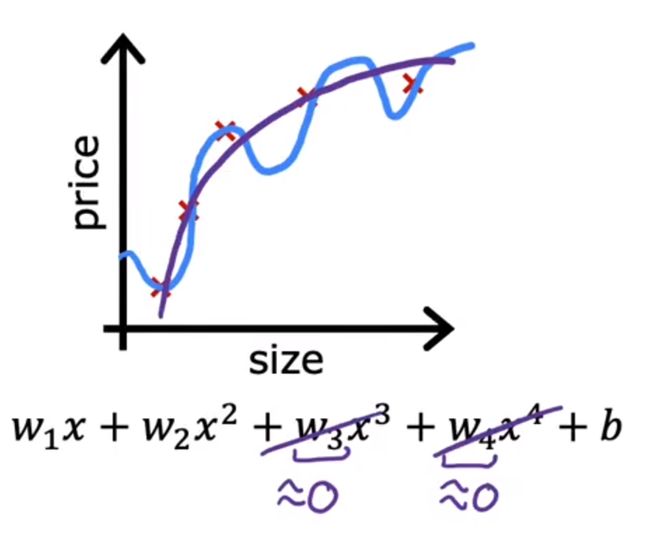
• 公式

λ：正则化参数，需要人工给定

λ不能过大（所有项都趋0），也不能过小（没有用）

1.正则化线性回归

公式：

将梯度下降算法代入：

只将w正则化

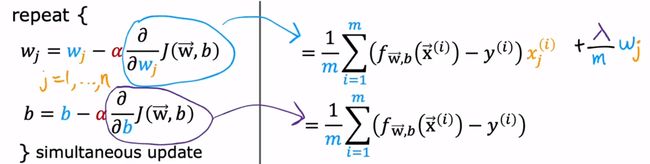
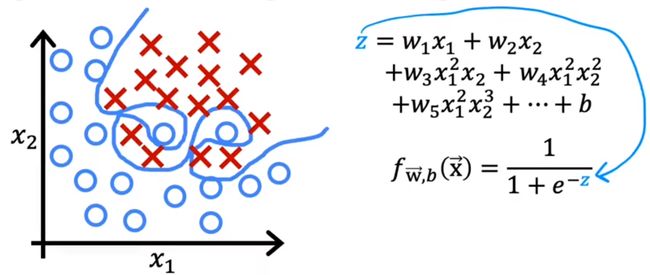
2.正则化逻辑回归

过拟合逻辑回归图

公式：

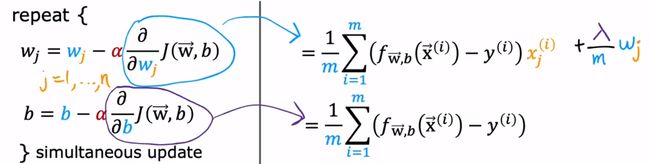
将梯度下降算法代入：

只将w正则化

**注：**此处的fw,b和线性回归的不同
$$f_{w,b}(x)=\frac{1}{1+e^{-(w\cdot x)+b}}$$