2023.4.11
文章目录
- 实现key前面的数都小于等key,key后面的数都大于等于key
-
- 1:前后指针法:
- 2:挖坑法
- 3:单指针法(左神)
- 辗转相除法求最大公约数
- 快速排序的递归写法
- 快速排序的非递归写法
实现key前面的数都小于等key,key后面的数都大于等于key
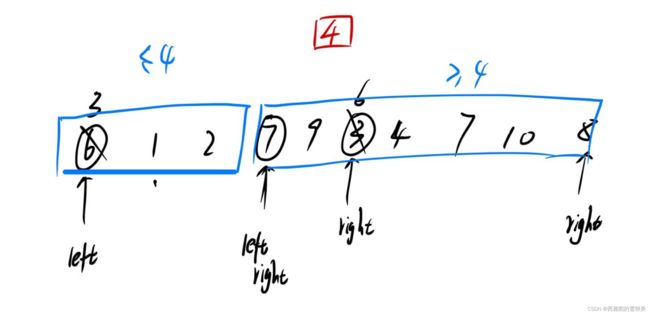
1:前后指针法:
public static void Sort(int[] array,int L,int R,int key) {
int left = L;
int right = R;
//确保key左边的都小于等于key,右边的都大于等于key
while(left < right) {
while (left < right && array[right] >= key) {
// 注意这里的等号要加 否则陷入死循环
right--;
}
//出循环之后right所指的数一定小于key
while(left < right && array[left] <= key) {
left++;
}
//出循环之后left所指的数一定大于key
swap(array,left,right);
}
//这样left后面的数一定大于等于key,left前面的数一定小于等于key
}
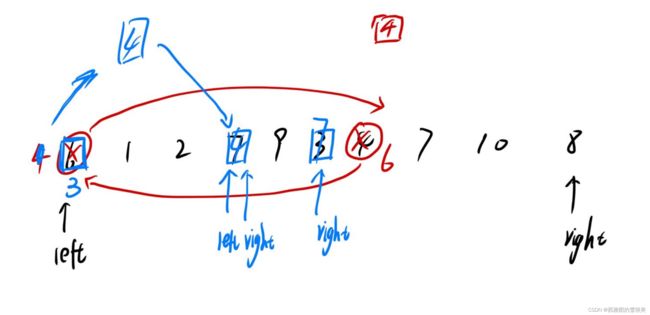
2:挖坑法
public static void sort(int[] array,int index) { // index是你的key的下标
swap(array,0,index); // 把key的值尽量往前方,重点。
int key = array[0];
int right = array.length-1;
int left = 0;
while(left < right) {
while(left < right && array[right] >= key) {
/**
这里加left < right 这个限制条件而不是right >= 0,
是因为如果出现right-- ,right小于left时候,此时还不会执行最外层while判断
,然后进行swap交换,这是错误的。
而且left < right这个条件比right >= 0 要严苛
*/
right--;
}
//出循环之后right所指的数一定小于key,去填left处的坑
swap(array,left,right);
while(left < right && array[left] <= key) {
left++;
}
//出循环之后left所指的数一定大于key,去填right处的坑
swap(array,left,right);
}
/**
1:最后right == left,right所经过的地方都是 >= key的
left所经过的地方都是 <= key的,
2:而且left与right相遇的时候一定有一个还是坑,所以相遇的地方就是个坑,直接把key放进去
3:当right停下的时候,left所指的地方是坑,当left停下的时候,right所指的地方是坑,
总之left与right来回交替着填坑。
*/
array[left] = key;
}
public static void swap(int[] array, int i,int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
重点:
之所以将你的key尽量的往前放是因为,当你的key在前面的时候,你从后往前找到小于key的数放在前面,
从前往后找找到大于key的数放在后面,这样前面的数都是小于key的后面的数都是大于key的,数不会乱。
如果你要找的key在中间,然后放数,数就会乱。
总之,将你要找的key放在最前面,然后先从后往前找,在从前往后找,循环进行,直到left = right
保证right所经过的数都 >= key , left所经过的数都小于等于key.
3:单指针法(左神)
// 思路
// 1:less只吃小于划分值的数,more只吃大于划分值的数,所以要保证less往前走的时候其前面的数要小划分值,more往前走的时 候其前面的数要大于划分值。
// 2:根据1这一特性,当index找到小于划分值的数时,就与less前面的数交换,将小数扔到less前面, 同理当index找到大于划分值的数时,就与more前面的数交换,将大数扔到more前面。
// 3:当index指向等于划分值的数时,直接跳过就行。
// 4:这样两边一起向中间挤,最终剩下的就是等于划分值的数。
// 心得
// less走的时候,其前面的数永远时小于划分值的,同理more前面永远是大于划分值的。
package algorithmbasic.class6;
// 荷兰国旗问题
public class netherlandsFlag {
// arr[L...R] 玩荷兰国旗问题的划分,以arr[R]做划分值
// arr[R]
public static int[] netherlandsFlag(int[] arr, int L, int R) {
if (L > R) {
return new int[]{Integer.MIN_VALUE, Integer.MIN_VALUE};
}
if (L == R) {
return new int[]{L, R};
}
int less = L - 1;
int more = R;
int index = L;
while (index < more) {
if (arr[index] < arr[R]) {
//swap(arr, index, less + 1);
//less++;
//index++;
swap(arr, index++, ++less);
} else if (arr[index] > arr[R]) {
// 这个地方index不可以++,因为当前新换过来的数还并没有进行判断。
swap(arr, index, --more);
} else {
index++;
}
}
// 最后将划分值与more位置的的数进行交换。
swap(arr, R, more);
return new int[]{less + 1, more};
}
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
辗转相除法求最大公约数
最大公约数:
辗转相除法求最大公约数:
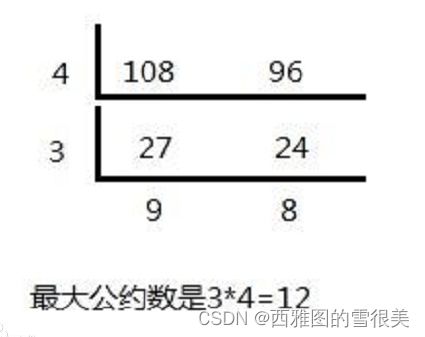
例一:
108 / 96 商:1 余:12
96 / 12 商:8 余:0
则最大公约数是:12
例二:
118 / 96 商:1 余:22
96 / 22 商:4 余:8
22 / 8 商:2 余:6
8 / 6 商:1 余:2
6 / 2 商:3 余:0
则最大公约数是2
辗转相除法的计算原理:
我们先计算出a除以b的余数c,把问题转化成求出b和c的最大公约数;然后计算出b除以c的余数d,把问题转化成求出c和d的最大公约数;再然后计算出c除以d的余数e,把问题转化成求出d和e的最大公约数…以此类推,逐渐把两个较大整数之间的运算简化成两个较小整数之间的运算,直到两个数可以整除,或者其中一个数减小到1为止。
快速排序的递归写法
// 思路:
// 1:设立一个划分值x,x的放右边,这样x值的位置就排好了,并且左边都是小于x的,右边都是大于x的。
// 2:然后递归,将左边
// 3:最后当递到一个数的时候就排好序了。
// 注意:
// 1:划分值的选择,划分值的选择是非常重要的。理想状态下每次最好的划分值x是:小于x的部分与大于x的部分个数是一样的。
// 这样尽可能的进行二分。时间复杂度保证为:N*logN,划分值偏太多会导致时间复杂度变为N^2
swap(arr, L + (int) (Math.random() * (R - L + 1)), R);
// 在arr[L , R]范围上随机找一个数作为划分值,虽然每一次都不均匀,但经过数学家计算,时间复杂度是NlogN. 图一:
// 2:递归的截止条件是
if (L >= R) {
return;
}
// 理想状态下是即有左组又有右组,这样尽可能的满足二分,但是有时会出现只有左组没有右组,或是只有右组没有左组的情况
// 如图2:当L = R时就一个数已经有序了不用再排了,直接返回。当L > R时,说明没有左组或者没有右组,也直接返回就行,不 返回就会报错。
// 心得:
// 递归的截止条件是
if (L >= R) {
return;
}
// 可能会出现没有左组huo'zh
图一:
图二:
package algorithmbasic.class6;
// 快排3.0 递归版本
public class quickSort {
public static void quickSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
process(arr, 0, arr.length - 1);
}
// 递归函数:将arr[L , R]范围排有序
public static void process(int[] arr, int L, int R) {
// 注意点2
if (L >= R) {
return;
}
// 注意点1
swap(arr, L + (int) (Math.random() * (R - L + 1)), R);
int[] equalArea = netherlandsFlag(arr, L, R);
int el = equalArea[0];
int er = equalArea[1];
process(arr, L, el - 1);
process(arr, er + 1, R);
}
// arr[L...R] 玩荷兰国旗问题的划分,以arr[R]做划分值
// arr[R]
public static int[] netherlandsFlag(int[] arr, int L, int R) {
if (L > R) {
return new int[]{Integer.MIN_VALUE, Integer.MIN_VALUE};
}
if (L == R) {
return new int[]{L, R};
}
int less = L - 1;
int more = R;
int index = L;
while (index < more) {
if (arr[index] < arr[R]) {
//swap(arr, index, less + 1);
//less++;
//index++;
swap(arr, index++, ++less);
} else if (arr[index] > arr[R]) {
swap(arr, index, --more);
} else {
index++;
}
}
swap(arr, R, more);
return new int[]{less + 1, more};
}
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
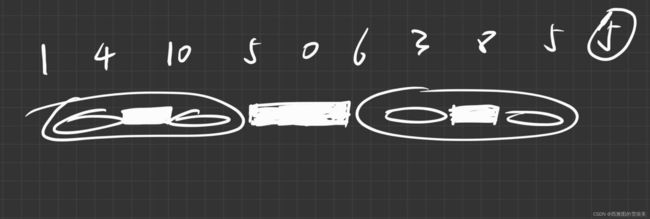
快速排序的非递归写法
// 思路:
// 1:主要是用栈来实现递归。
// 具体步骤:先通过netherlandsFlag方法将整个arr[L , R]区间划分成区域1与区域2。将区域2压入栈中,再将区域1压入栈 中,将区域1弹出,再通过netherlandsFlag方法将区域1划分成区域3与区域4,将区域3压入栈中,再将区域4压入栈中,再将 区域4弹出,再通过netherlandsFlag方法将区域4划分成区域5与区域6,将区域5压入栈中,再将区域6压入栈中,如此往复,我 们会发现压入栈中的都是区域的右半部分,当左半部分走到头的时候,递归就会“归”回来,将右半部分都完成。
图一:
package algorithmbasic.class6;
import java.util.Stack;
// 快速排序的非递归版本
public class quickSort2 {
// 栈中存储的数据结构
// 要处理的是什么范围上的排序
public static class Op {
int l;
int r;
public Op(int l, int r) {
this.l = l;
this.r = r;
}
}
public static void quick(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
int N = arr.length;
Stack<Op> stack = new Stack<>();
// 划分值随机选择,使复杂度趋于N*logN
swap(arr, (int) (Math.random() * N), N - 1);
int[] equalArea = netherlandsFlag(arr, 0, N - 1);
int el = equalArea[0];
int er = equalArea[1];
stack.push(new Op(er + 1, N - 1));
stack.push(new Op(0, el - 1));
while (!stack.isEmpty()) {
Op op = stack.pop();
// 先放右组后放左组
// 当只有左组没有右组的时候,就会出现 : er + 1 > op.r 即:L > R
// 当只有右组没有左组的时候,就会出现 :op.l > el - 1 即:L > R 图一
// if之所以放在这个地方,而不是直接包含着Op op = stack.pop();原因是,不符合的区间需要被弹出。
if (op.l < op.r) {
swap(arr, (int) (op.l + Math.random() * (op.r - op.l + 1)), op.r);
equalArea = netherlandsFlag(arr, op.l, op.r);
el = equalArea[0];
er = equalArea[1];
stack.push(new Op(er + 1, op.r));
stack.push(new Op(op.l, el - 1));
}
}
}
// arr[L...R] 玩荷兰国旗问题的划分,以arr[R]做划分值
// arr[R]
public static int[] netherlandsFlag(int[] arr, int L, int R) {
if (L > R) {
return new int[]{Integer.MIN_VALUE, Integer.MIN_VALUE};
}
if (L == R) {
return new int[]{L, R};
}
int less = L - 1;
int more = R;
int index = L;
while (index < more) {
if (arr[index] < arr[R]) {
//swap(arr, index, less + 1);
//less++;
//index++;
swap(arr, index++, ++less);
} else if (arr[index] > arr[R]) {
swap(arr, index, --more);
} else {
index++;
}
}
swap(arr, R, more);
return new int[]{less + 1, more};
}
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}