多项式模型与多项式拟合

3. 多项式模型 (一元多次方程)

3.1 多项式拟合

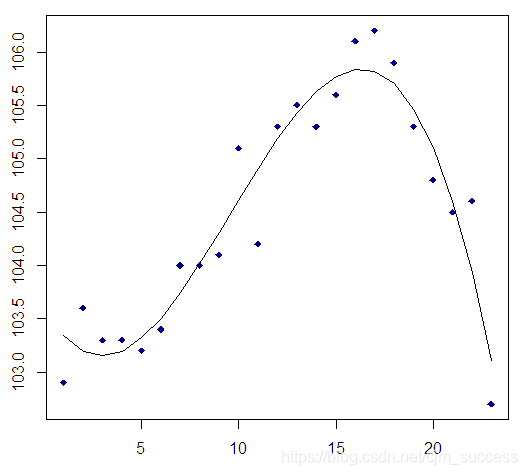
在有些数据分布中，使用一条曲线比直线能更好拟合数据，这就需要用到多项式拟合。如下图所示分布：

多项式的一般形式：
$$y=p_0{x}^n+p_1{x}^{n-1}+p_2{x}^{n-2}+p_3{x}^{n-3}+...+p_n$$
多项式拟合的目的是为了找到一组 $p_0,p_1,...,p_n$，使得拟合方程尽可能的与实际样本数据相符合。

假设拟合得到的多项式如下：
$$f(x)=p_0{x}^n+p_1{x}^{n-1}+p_2{x}^{n-2}+p_3{x}^{n-3}+...+p_n$$
则拟合函数与真实结果的差方如下：
$$loss=(y_1-f(x_1){)}^2+(y_2-f(x_2){)}^2+...+(y_n-f(x_n){)}^2$$
那么多项式拟合的过程即为求取一组$p_0,p_1,...,p_n$, 使得loss的值最小。在程序中，多项式可以表示为一个数组，格式如下：

f = [-6, 3, 8, 1]

表示多项式为：
$$y=-6x^3+3x^2+8x+1$$

3.2 多项式API

Python中, 可以用 numpy.polyfit() 函数进行多项式拟合

X = [x1, x2, ..., xn]
Y = [y1, y2, ..., yn]
# 根据一组样本，并给出最高次幂，求出拟合系数
np.polyfit(X, Y, 最高次幂)	# 得到的是一个一维数组

其他多项式运算相关函数

# 根据拟合系数与自变量求出拟合值, 由此可得拟合曲线坐标样本数据 [X, Y']
np.polyval(P, X)->Y'

# 多项式函数求导，根据拟合系数求出多项式函数导函数的系数
np.polyder(P)->Q 

# 已知多项式系数Q 求多项式函数的根（与x轴交点的横坐标, 即波峰波谷）
xs = np.roots(Q)

# 两个多项式函数的差函数（对应系数相减）的系数（可以通过差函数的根求取两个曲线的交点）
Q = np.polysub(P1, P2)

3.3 苹果股价案例

打开文件, 查看苹果股票的日期与收盘价格

import pandas as pd
import numpy as np

data = pd.read_csv('aapl.csv',					# 导入文件
                   header=None,
                   names=['dates','close'])		# 日期 & 当日收市股价
print(data)
                """
                    dates		close
                0	2011-01-28	336.10
                1	2011-01-31	339.32
                2	2011-02-01	345.03
                3	2011-02-02	344.32
                4	2011-02-03	343.44
                ...		...		...
                27	2011-03-09	352.47
                28	2011-03-10	346.67
                29	2011-03-11	351.99
                """

为了方便进行数学运算, 需要把日期改为数字格式, 可以用2011-01-01为0, 计算每个日期距离2011-01-01的天数为日期值 delta

data['delta'] = data['dates'] - pd.to_datetime('2011-01-01')
data['delta'] = data['delta'].dt.days
print(data)
                """
                    dates		close	delta
                0	2011-01-28	336.10	27
                1	2011-01-31	339.32	30
                2	2011-02-01	345.03	31
                3	2011-02-02	344.32	32
                ...		...		...		...
                """

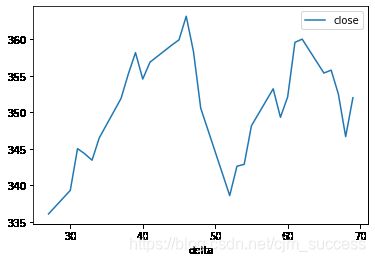
画出close和delta的图表

data.plot(x='delta', y='close')

a) 多项式拟合

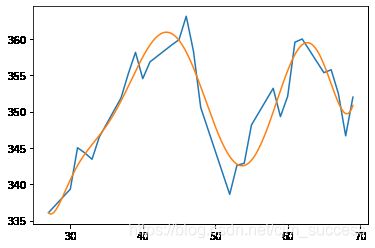
针对股票价格, 用polyfit()函数进行多项式拟合

# polyfit函数, 需要(x数据, y数据, deg=项数)三个必要参数, 
p = np.polyfit(data['delta'], data['close'], 5)
print(p)
# array([-1.97919911e-05,  4.66447608e-03, -4.27249275e-01,  1.89446747e+01, -4.05027302e+02,  3.67749979e+03])
# 得到的是多项式函数的系数

b) 计算拟合值

根据多项式函数, 可以用polyval()函数计算拟合值

我们可以计算200个拟合值, 画出曲线图 (折线图的点变多了, 就变成曲线图了~)

# 将delta从最小值到最大值之间平均分割200个数, 得到一个一维数组
xs = np.linspace(data['delta'].min(), data['delta'].max(), 200)
# linspace函数是创建数值序列的工具. 
# 需要指定间隔起始点、终止端，以及指定分隔值总数（包括起始点和终止点）；最终函数返回间隔类均匀分布的数值序列

# polyval函数, 根据拟合系数与自变量求出拟合值, 由此可得拟合曲线坐标样本数据 
# 根据函数系数p(用polyfit函数计算得到), 以及x的值序列xs(用linspace函数计算得到), 求出y值序列ys
ys = np.polyval(p, xs)

# 画出源数据图
plt.plot(data['delta'], data['close'])
# 画出多项式拟合图
plt.plot(xs, ys)

c) 欠拟合 & 过拟合

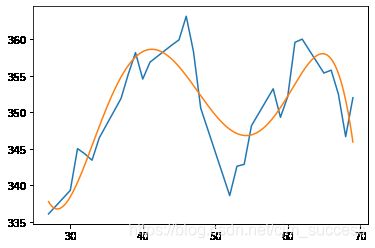
欠拟合:

• 欠拟合是指模型拟合程度不高，数据距离拟合曲线较远，或指模型没有很好地捕捉到数据特征，不能够很好地拟合数据
• 上图的拟合就较为欠缺

过拟合:

• 为了得到一致假设而使假设变得过度严格称为过拟合
• 一个假设在训练数据上能够获得比其他假设更好的拟合， 但是在训练数据外的数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。出现这种现象的主要原因是训练数据中存在噪音或者训练数据太少

调整多项式的最高次幂来调整拟合度

p = np.polyfit(data['delta'], data['close'], 20)				# 将最高次幂调整为20
xs = np.linspace(data['delta'].min(), data['delta'].max(), 200)
ys = np.polyval(p, xs)
plt.plot(data['delta'], data['close'])
plt.plot(xs, ys)

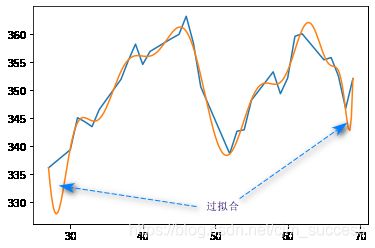
根据下图可以看得出来, 多项式函数可以很好的拟合股价波动了, 但是在一些位置出现了过拟合

继续调整多项式的最高次幂来找到最佳的拟合函数

p = np.polyfit(data['delta'], data['close'], 9)				# 将最高次幂调整为9
xs = np.linspace(data['delta'].min(), data['delta'].max(), 200)
ys = np.polyval(p, xs)
plt.plot(data['delta'], data['close'])
plt.plot(xs, ys)

d) 函数趋势

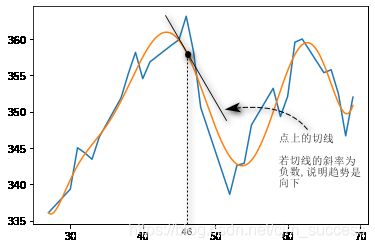
得到某一时刻股价的趋势 (涨/跌)
polyder函数可以根据拟合系数求出多项式函数导函数的系数

# polyder()函数用于多项式求导
q = np.polyder(p)

# 当x=46时, 判断是涨还是跌
# 将46放入导数函数
k = np.polyval(q, 46)
print(k)		# -1.9249425322705065
# k为负数表示, 当x=46时, 股价的趋势是下降的

e) 波峰波谷

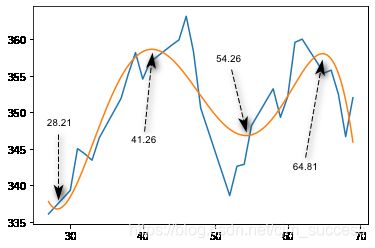
如何求出波峰波谷? ==> 函数切线斜率为0的位置 ==> 即导数函数的根

xs = np.roots(q)
print(xs)
# array([64.81228477, 54.26409333, 41.25554414, 28.20802013])
# 求出的是x轴的值

线性函数或多项式函数只是对于已经发生的数据继续拟合, 无法用于预测未发生的