什么是有理数和无理数？

目录

1. 实数(Real Number)

2. 比率数(Rational Number，姑且称为“比率数”)(有理数？)

2.1 比率数的引出和定义

2.2 比率数的图形表示

2.3 密度(Density)

3. 非比数(Irrational Number，姑且称为“非比数”)(无理数？)

3.1 非公度量(非比量)(Incommensurable Quantities)

3.2 非比数定义(Irrational Number)(无理数？)

---

1. 实数(Real Number)

实数(real number):对自然数的扩充后形成的数，使我们可以描述度量的连续渐变特性(而不是仅针对单个的计数),这种扩展数我们称为数联集(number continuum，或称，“数的连续统一体”、“数连续统”)，或者称为“实数”系统(“real number”这个名称，虽然不是学科专用描述词，但已被广泛接受，“real”即“真实”，从客观计数衍生而来)。

2. 比率数(Rational Number，姑且称为“比率数”)(有理数？)

2.1 比率数的引出和定义

对于我们来说，自然数被认为是已知的。在十进制系统中，加数和乘法满足一定的定律。

交接律(commutative laws)

a + b = b + a, ab = ba

结合律(associative laws)

(a + b) + c = a + (b + c)

(ab)c = a(bc)

分配律(distributive law)

a(b + c) = ab + ac

相消律(cancellation law)

a + c = b + c 意味着 a = b

等等。

对于加法和乘法而言，在自然数的领域内，其逆向操作(减法和除法)并非总是成立；我们不能做到——从1减去2，用1除以2，结果仍然是自然数。为了突然这种限制，使其逆向操作成为可能，人类被迫发明了数字“0”，负整数，以及分数。所有这些分类总称为比率数(Rational Number)分类或比率数集合；所有这些比率数都可以通过计算的“比率数运算(rational operations)”而获得，即，通过加减乘除而获得。

需要特别地注意，在这里，“rational”这个词不是“合理的,有理由的(reasonable)”的意思，也不是“合乎逻辑的(logical)”的意思，而是派生于单词“ratio”,其词义为“两个量纲(magnitudes)的相对比率”(译注：同量纲的事物相比才有意义)。(译注：因此，将“Rational Number”译为“有理数”，不管是从字面意义还是从逻辑意义上讲，都是一个严重的错误。同理，“Irrational Number”译为“无理数”也同样不妥。)

比率数总是可以写成   (其中，p和q为整数，且q≠0 )的形式。我们可以使这种表示具有唯一性，具体做法是，要求p是正数，且p和q为没有大于1的公因子。(译注：这揭示了比率数的本质。) 

在比率数领域内，所比率数运算，加法、乘法、减法和除法(除以零除外)都可以执行并再次产生比率数。正如我们从初等算术中了解到的，比率数运算遵循与自然数运算相同的法则：因此比率数以完全直接的方式扩展了正整数系统。

2.2 比率数的图形表示

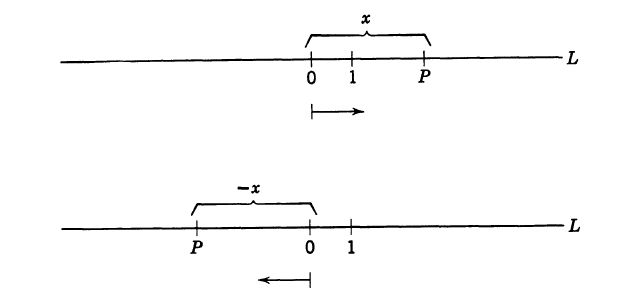
实际上，比率数可以通过一条直线L上的点来表示，这条直线称为数轴(number axis)，如下图1.1。采用直线L上任意一点作为原点或点0，另外的任意一点作为点1，我们使用这两点之间的距离作为刻度(scale)或测量单位，并将从 0 到 1 的方向定义为“正”。这条被赋予了方向的直线称为有向直线。通常将L描绘为点 1 在点 0 的右侧。L上任意一点 P 的位置完全由两条信息决定：P 到原点 0 的距离和从 0 到 P 的方向(在 0 的右边或左边)。 L上表示正比率数的点 P 位于 0 右侧的 x 个单位处。负比率数 x 由 0 左侧的点 - x 个单位表示。在任何一种情况下，从 0 到任意点的距离表示x的的绝对值，记作|x|，我们有

注意，|x|从来不为负或为零(仅当x = 0时为0)。

 -------------------------------------------------------图1.1 数轴---------------------------------------------

从初等几何学我们记得，使用尺子(ruler)和圆规(compass)可以将单位长度细分为任意数量的相等部分。由此可见，可以构造任何比率长度，因此可以通过纯几何方法找到表示比率数 x 的点。

按这种方式，我们通过 L 上的点(比率点)获得了比率数的几何表示。与我们对点 0 和 1 的表示法一致，我们冒昧地用相同的符号 x 表示比率数和L上的对应点。

对于比率数而言，x < y 的关系，在几何上意味着点x位于点y的左侧，这样的话，两点之间的距离便是(y - x)个单位。假如 x > y，则距离为(x - y)个单位。在这两种情况下，这两者之间的距离都为为| y - x|个单位，并且仍然是一个比率数。

直线L上具有站点a和b且a < b的一段，称为区间(interval)。具有0和1端点的这特殊的一段，称为单位区间(unit interval)。假如端点包含在区间中，我们说这个区间是闭区间(closed interval),假如端点不包含在区间中，我们说这个区间是开区间(open interval)。开区间用(a, b)表示，由a < x < b 之间的所有x点构成，即由“介于”a和b之间的所有点构成。闭区间用[a, b]表示，由a ≤ x ≤ b 之间的所有x点构成。在这两种情况下，区间的长度都是(b - a)个单位。

整数0、±1、±2、……对应的点将数轴细分为单位长度的区间。在直线L上的每一个点，或是端点，或是某一个细分区间上的内部点。如果我们进一步细分每个区间成q等分，则按照比率数的记法形式(p/q)，我们就获得一个将L的单位长度再次划分成单位长度为(1/q)的子区间(每个单位长度内部再等分)。则，直线L的每个点，或者是形如(p/q)的比率点，或者是介于后续(p/q)和(p + 1)/q 之间的比率点(如图1.2所示)。因此二次划分的子区间的间隔是(1/q),它遵循的原则是，我们可以求得一个比率点(p/q)，它距离P点的距离不会超过(1/q)个单位。只要我们乐意，我们可以将数(1/q)可以划分得足够小，只要选择足够大的正整数q即可。例如，可以选取  (其中，n是任意自然数)，我们可以求得一个“十进制分数”  ,其距离P点的距离不会超过 () 个单位。尽管我们不能断言L上的每一个点都是比率点，但我们至少可以看到比率点可以任意靠近 L 的任何点 P。

-----------------------------------------------------------------图1.2 -----------------------------------------------------

2.3 密度(Density)

    直线L上已知点P与比率点的接近度可以说成：比率点在数轴上的密度(density)。

显然，甚至更小的比率数集都是有密度的，比如，点   ，对于所有自然数n和整数p。

密度意味着在任意两个不同的比率点 a 和 b 之间存在无限多的其他比率点。 特别是，a 和 b之间的点  ，对应于数a 和 b的算术平均值，也是比率数。取a和 c ， b 和 c的中点，并以这种方式继续，我们可以获得a 和 b之间的任意数量的比率点。

可以使用比率点以任意精度定位 L 上的任意点 P。 乍一看，通过引入比率数似乎已经完成了通过数定位P的任务。毕竟，在物理现实中，从来没有绝对精确地给出或知道其数量，而总是只有一定程度的不确定性，因此也可以认为是用比率数来衡量的。

3. 非比数(Irrational Number，姑且称为“非比数”)(无理数？)

3.1 非公度量(非比量)(Incommensurable Quantities)

尽管比率数是稠密的，但它们不足以用作数的度量的理论基础。比率(ratio)为比率数的两个量称为可公度的(commensurable，或称可比的，可通约的)，因为它们可以表示为一个公共单位的整数倍。早在公元前五六世纪，古希腊数学家和哲学家做出了一个令人惊讶和激动人心的发现，即存在与给定单位不可比的量(commensurable quantities)。 特别是，存在不是给定单位线段的比率数倍数的线段。

很容易举出与单位长度不可公度的长度的例子：具有单位长度的正方形的对角线l。按照毕达哥拉斯定理(Pythagoras),这个长度l的平方必须等于2。因此，如果l是比率数，并且其结果可以表示成(p/q)(其中，p和q是正整数)的形式，即l = p/q，则我们应该得到  。我们可以假设p和q没有公因数，因为这些公因数可以从一开始就被抵消。按照上面的等式， 一定是一个偶数；因此，p本身一定是一个偶数，假定p = 2p’ 。用2p’代入上面的等式，得到  或  ；结果就是， 是一个偶数，因此q也是一个偶数。这就证明了p和q还有公因子2。然而，这与我们的假设p和q没有公因数矛盾。因此，假设对角线可以表示成分数(p/q)的形式会导至矛盾，这种假设不成立。

通过一个典型的案例推理，间接地证明了符号  并不对应任何比率数。另一个例子是π——圆的周长与其直径的比值。证明π是一个非比率数非常复杂，并且仅在现代才能做到(Lambert, 生于1761年，德国数学家，证明了π和e为不可通约量)。很容易找到很多非通约量；事实上，在某种意义上，非通约量远比通约量更为普遍。

3.2 非比数定义(Irrational Number)(无理数？)

由于比率数系统不足以用于几何学，因此有必要发明新数作为不可通约量的度量：这些新数称为“非比数”。 古希腊人并不强调抽象的数概念，而是将线段等几何实体视为基本元素(译注：在他们的数学思想中，一切皆几何)。 他们以纯粹的几何方式开发了一个逻辑系统，用于处理和操作不可通约量以及可通约(可比量)量。这个由毕达哥拉斯(Pythagoreans)学派发起的重要成就，被Eudoxus大大推进，并在Euclid著名的<<数学原理>>(Elements)中得到了详细的表述。在现代，数学是在数的概念而非几何概念的基础上被重新创造和极大扩展的。随着解析几何的引入，人们对数与几何量之间古老关系的重视发生了逆转，经典的不可公约理论几乎被遗忘或忽视。人们理所当然地假设数轴上的每一点都对应一个比率数或非比数，并且这个“实”数的总和遵循与比率数相同的算术定律。直到后来，在 19 世纪，Dedekind 的一本非凡的小册子才让人们感觉到并最终完全满足了证明这种假设的必要性，这本小册子至今仍令人着迷(R. Dedekind所著<>(关于数的论文集)中的“Nature and Meaning of Number(数的特征和意义)”，London和Chicago, 1901年出版，这些论文中的第一篇“Continuity and Irrational Numbers(连续性和非比数)”详细介绍了实数的定义和运算法则。Dover, New York,1964年重印时，改书名为<>(数论论文集))。

实际上，Dedekind表明，从Fermat和Newton到Gauss和Riemann的所有伟大数学家所采用的“朴素(naive)”方法是正确的：实数系统(作为线段长度的符号，或以其他方式定义)是一个一致和完整的科学测量工具，在这个系统中，比率数系统的计算规则仍然有效。

内容来源：

<>，作者：Richard Courant,Fritz John