Codeforces Round #686 (Div. 3) (题解)
传送门

 题目大意:
题目大意:
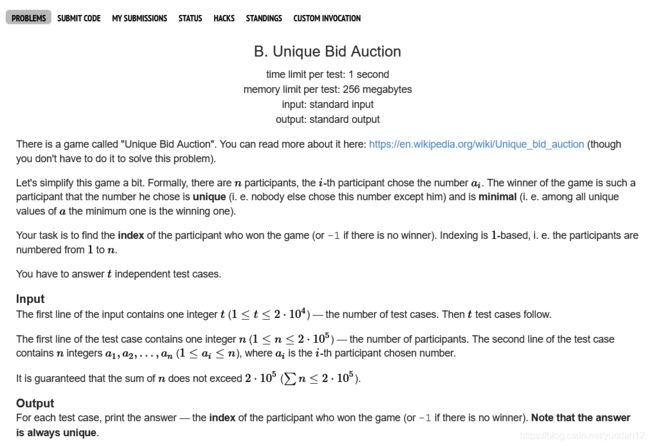
给一个自然数n,给出1~n的排序,使得第i个位置上的a[i]不等于i
思路:
错误想法:逆序输出,因为5,4,3,2,1中3的位置上还是3
正确思路:将头结点放到尾节点。例如:2,3,4,5,1
#include
using namespace std;
#define LL long long
#define IO ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
void solve()
{
int n;
cin >> n;
for(int i = 2;i <= n;++i)
{
cout << i << " ";
}
cout << 1;
cout << endl;
}
int main()
{
IO;
int t;
cin >> t;
while(t--){
solve();
}
return 0;
}
题目总结:
思维水题,在做题的时候没有主要到hack信息wrong了一发,太可惜了。
思路:
用map存储,然后遍历为1的map值。
#include
using namespace std;
#define LL long long
#define IO ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
const int maxn = 1e5+5;
struct stu{
int value;
int id;
}a[maxn*2];
bool cmp(struct stu a,struct stu b)
{
return a.value < b.value;
}
void slove()
{
int n;
cin >> n;
for(int i = 1;i <= n;++i){
cin >> a[i].value;
a[i].id = i;
}
sort(a+1,a+n+1,cmp);
bool si = false;
int i;
for(i = 1;i < n;++i)
{
if(a[i+1].value != a[i].value && !si) break;
else if(a[i+1].value == a[i].value) si = true;
else si = false;
}
if(si) cout << -1 << endl;
else cout << a[i].id << endl;
}
int main()
{
IO;
int t;
cin >> t;
while(t--){
slove();
}
return 0;
}
题目总结:
map遍历的练习
传送门

 题目大意:
题目大意:
给出n个数,可以选一个x然后从n个数据中删除l->r的所有数据。数据中心不包括x,使得最后剩下的数据只有x,求最小删除次数。
思路:
用map存储,然后寻找的最小的map值。
注意尾部数据需要净化
或者使用unique全局净化数据
#include
using namespace std;
#define LL long long
#define IO ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
const int maxn = 1e5+5;
int a[maxn*2];
map mp;
void slove()
{
mp.clear();
int n;
cin >> n;
bool si = false;
for(int i = 1;i <= n;++i)
{
cin >> a[i];
}
while(n > 0)
if(a[n] == a[n-1]) n--;
else break;
for(int i = 1;i <= n;++i)
{
if(i == 1) mp[a[i]] = 1;
else if(a[i] == a[i-1]) continue;
else if(i == n){
si = true;
if(mp[a[i]] != 0) continue;
else mp[a[i]] = 1;
}
else {
si = true;
if(mp[a[i]] == 0) mp[a[i]] = 2;
else mp[a[i]]++;
}
}
if(!si) cout << 0 << endl;
else {
int mi = 2e5+10;
for(map::iterator it = mp.begin();it != mp.end();it++)
{
//cout << it->first << " " << it->second << endl;
mi = min(mi,it->second);
}
cout << mi << endl;
}
}
int main()
{
int t;
cin >> t;
while(t--){
slove();
}
return 0;
}
题目总结:
学到了unique函数,和数据净化思路
传送门

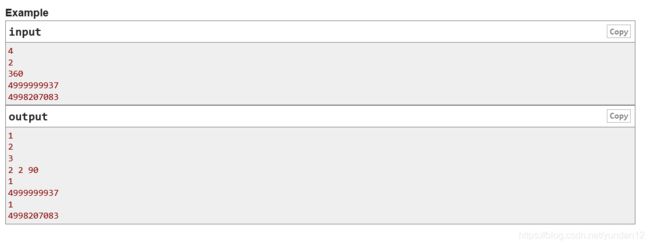
题目大意:
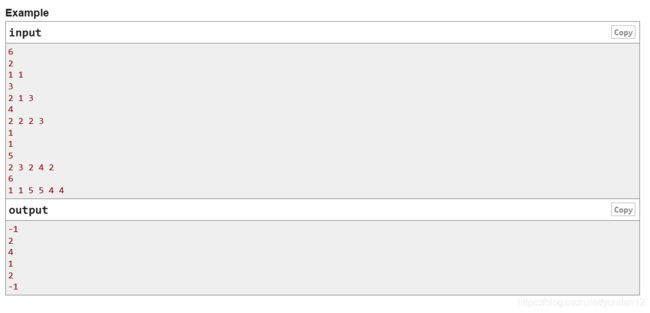
寻找k个数使得a1a2a3*···ak
而且第i个数可以整除前i-1个数的任意一个
寻找最长的k
输出k,并且输出a1->ak
思路:
寻找最长的相同因子序
例如:360->2 2 2 3 3 5
k = 3
ans = 2 2 2335
2 2 3 3 3 3 3 3 3 5
k = 7
ans = 3 3 3 3 3 3 2235
#include
using namespace std;
#define LL long long
void solve()
{
LL n,m;
cin >> n;
m = n;
LL ma = 0,cnt = 0,l = 0;
for(LL i = 2;i <= sqrt(n);++i)
if(n%i == 0){
while(n%i == 0){
cnt++;
n /= i;
}
if(cnt > ma){
ma = cnt;
l = i;
}
cnt = 0;
}
if(ma == 0 || ma == 1) {
cout << 1 << endl;
cout << m << endl;
}
else {
cout << ma << endl;
for(int i = 1;i < ma;++i)
cout << l << " ";
LL ans = m/(LL)(pow(l,ma-1));
printf("%lld\n",ans);
}
}
int main()
{
int t;
cin >> t;
while(t--){
solve();
}
}
题目总结:
思维水题,不断整除cnt计数
思路:
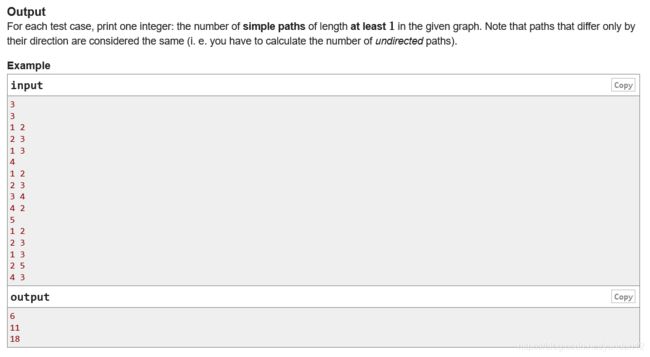
Consider some tree hung on a vertex v on a cycle. There is only one path between each pair of its vertices (including the root which is a vertex v). So, if the tree has cntv vertices, then cntv(cntv−1)2 paths are added to the answer. What about paths that go out of a tree? Let’s assume that there are cntv⋅(n−cntv)
such paths (yeah, we counted only a half of actual paths from this component but this is fine). When we consider other trees, we will take into account the other half of paths.
This information can lead us to the conclusion that the only information we need to know about trees hanged on cycle vertices is the number of vertices in these trees. So, if we know cntv
for each vertex on a cycle, we can just calculate the answer as ∑v∈cyclecntv(cntv−1)2+cntv⋅(n−cntv). So how to find values cntv?
#include
using namespace std;
int N = 2e5+5;
void solve(){
int n;
int cnt[N];
queue p;
scanf("%d",&n);
vector< set > g(n+1);
for(int i = 1;i <= n;++i) cnt[i] = 1;
for(int i = 1;i <= n;++i)
{
int u,v;
cin >> u >> v;
g[u].insert(v);
g[v].insert(u);
}
for(int i = 1;i <= n;++i)
{
if(g[i].size() == 1)
p.push(i);
}
while(p.size()){
int v = p.front();
p.pop();
int to = *g[v].begin();
cnt[to] += cnt[v];
cnt[v] = 0;
g[v].clear();
g[to].erase(v);
if(g[to].size() == 1)
p.push(to);
}
long long res = 0;
for(int i = 1;i <= n;++i)
{
res += cnt[i] * 1ll * (cnt[i]-1)/2;
res += cnt[i] * 1ll * (n-cnt[i]);
}
cout << res << endl;
}
int main(){
int t;
cin >> t;
while(t--){
solve();
}
}
题目总结:
图论加数论
传送门

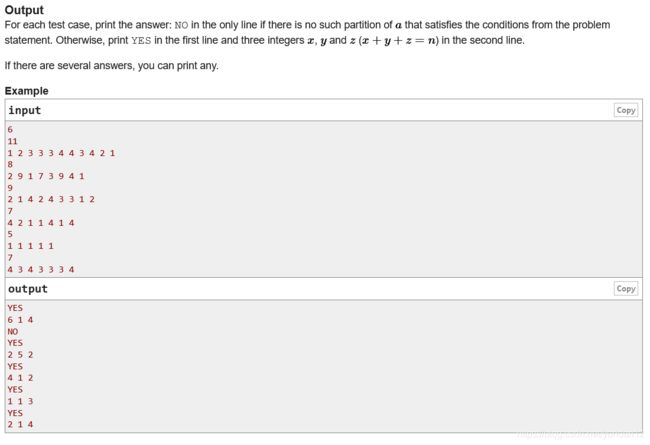
题目大意:
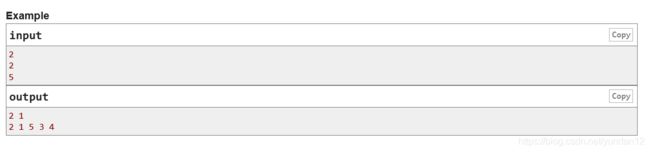
将n个数据分成三段,
使得max(l1,r1) = min(r1+1,r2) = max(r2+1,la);
思路:
线段树来记录左右的最大值
从最大数处开始左右贪心
#include
using namespace std;
const int maxn = 2e5+10;
struct node{
int l,r,v;
}p[maxn*4];
int z[maxn],y[maxn],a[maxn];
int T,n,tag;
void init(int u,int l,int r)
{
p[u] = {l,r,maxn};
if(l >= r) return ;
int mid = (l+r)>>1;
init(u << 1,l,mid);
init(u << 1 | 1,mid+1,r);
}
void pushup(int u)
{
p[u].v = min(p[u<<1].v,p[u<<1|1].v);
}
void modify(int u,int l,int r,int k)
{
if(p[u].l >= l && p[u].r <= r){
p[u].v = k;
return ;
}
int mid = (p[u].l + p[u].r) >> 1;
if(mid >= r) modify(u<<1,l,r,k);
else modify(u<<1|1,l,r,k);
pushup(u);
}
int quary(int u,int l,int r)
{
if(l > r) return maxn;
if(p[u].l >= l && p[u].r <= r)
return p[u].v;
int mid = (p[u].l + p[u].r) >> 1;
if(mid >= r)
return quary(u<<1,l,r);
else if(mid < l)
return quary(u << 1 | 1,l,r);
else
return min(quary(u<<1,l,r),quary(u << 1 | 1,l,r));
}
void solve(int x)
{
if(x >= n-1 || tag)
return ;
int l = x+2,r = n;
while(l <= r){
int mid = (l+r)>>1;
if(z[x] < y[mid])
l = mid + 1;
else if(z[x] > y[mid])
r = mid - 1;
else{
int k = quary(1,x+1,mid-1);
if(k == z[x] && !tag){
tag = 1;
cout << "YES" << endl;
cout << x << " " << mid-x-1 << " " << n-mid+1 << endl;
return ;
}
else {
if(k > z[x])
l = mid+1;
else
r = mid-1;
}
}
}
solve(x+1);
}
int main()
{
cin >> T;
for(int cnt = 1;cnt <= T;cnt++)
{
memset(z,0,sizeof(z));
memset(y,0,sizeof(y));
tag = 0;
cin >> n;
init(1,1,n);
for(int i = 1;i <= n;++i){
cin >> a[i];
modify(1,i,i,a[i]);
}
for(int i = 1;i <= n;++i)
z[i] = max(z[i-1],a[i]);
for(int i = n;i > 0;--i)
y[i] = max(y[i+1],a[i]);
solve(1);
if(!tag) cout << "NO" << endl;
}
return 0;
}
题目总结:
学到了线段树和二分