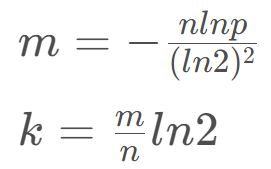哈希一刀流——布隆过滤器详解

传统艺能

小编是双非本科大二菜鸟不赘述，欢迎米娜桑来指点江山哦

非科班转码社区诚邀您入驻
小伙伴们，打码路上一路向北，彼岸之前皆是疾苦
一个人的单打独斗不如一群人的砥砺前行
这是和梦想合伙人组建的社区，诚邀各位有志之士的加入！！
社区用户好文均加精（“标兵”文章字数2000+加精，“达人”文章字数1500+加精）
直达： 社区链接点我

---

背景

听名字就有种洋玩意儿的高端感，但实际上用的十分广泛，在校招面经里面看到了有大厂在问布隆过滤器，这里我就说一下我的拙见：

在上手新游戏的时候，你想到一个很有逼格的昵称，但此时系统告诉你 “此昵称已被注册”，这个昵称的唯一性就是运用了哈希的布隆过滤器，他本质上是就是一个 key 的模型，他只需要判断对象是否存在过就行。

按照我之前的思路，这种问题就有两种方法：

方法一：用红黑树或哈希表将所有使用过的昵称存储起来，直接判断该昵称是否在红黑树或哈希表中即可，但红黑树和哈希表最大的问题就是浪费空间，当昵称数量非常多的时候内存当中根本无法 hold 住
方法二：虽然位图只能存储整型数据，但我们可以通过一些哈希算法将字符串转换成整型，比如BKDR哈希算法，我们只需要直接判断位图中该昵称对应的比特位是否被设置即可

虽然但是，使用位图的情况下，256 个字符串排列组合有无限种可能，而映射成 10 个数字的单元上，不论用何种哈希算法都是必定会出现大量冲突的，硬要使用的话，还会面临一个更大的问题：因为不同的字符串被映射成了相同的整型，此时就会出现$误判现象$，明明没有使用过的昵称也会被判定为已使用，于是$布隆过滤器$横空出世

概念

布隆过滤器是由布隆（Burton Howard Bloom）在1970年提出的一种紧凑的、比较巧妙的概率型数据结构，特点是高效地插入和查询

布隆过滤器其实就是位图的一个变形和延申，虽然无法避免哈希冲突，但我们可以想办法降低误判的概率；当一个数据映射到位图中时，布隆过滤器会用多个哈希函数映射到多个比特位，当判断一个数据是否在位图当中时，需要分别根据这些哈希函数计算出对应的比特位，比特位设置了代表着当前状态的默认值，设置为 1 则判定为该数据存在，这一点很类似于我们定义红黑数的节点颜色。

布隆过滤器使用多个哈希函数进行映射，目的就在于降低哈希冲突的概率，一个哈希函数产生冲突的概率可能比较大，但多个哈希函数同时产生冲突的概率可就没那么大了！

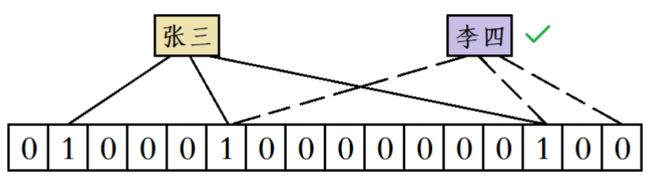
举个栗子：假设此时用三个哈希函数进行映射，那么 “张三” 这个昵称被使用后位图中会有三个地方会被置 1，当有人要使用 “李四” 这个昵称时，就算前两个哈希函数计算出来的位置都产生了冲突，但由于第三个哈希函数计算出的比特位的值为 0，此时系统就会判定“李四”这个昵称没有被使用过：

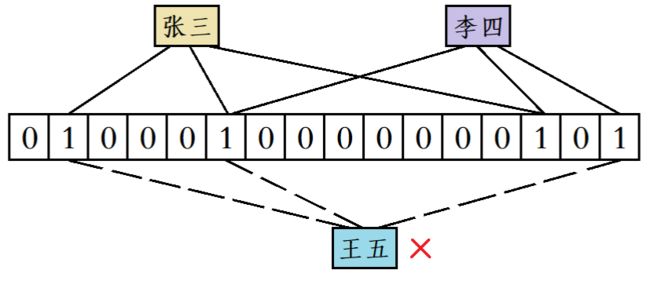
但是尽管如此，只要数据基数足够大，也会出现误判情况：比如此时又有人要使用 “王五” 这个昵称，虽然 “王五” 计算出来的三个位置既不和“张三”完全一样，也不和“李四”完全一样，但“王五”的三个位置都被“张三”和“李四”占用了，此时系统也会误判 “王五” 这个昵称已经被使用过了:

**敲黑板！**

虽然布隆过滤器判断一个数据存在可能是不准确的，因为这个数据对应的比特位可能被其他一个数据或多个数据占用了；但是布隆过滤器判断一个数据不存在却是准确的，因为如果该数据存在那么该数据对应的比特位都应该已经被设置为1了

误判控制

很显然，过小的布隆过滤器比特位很快就会都被设为 1，此时误判率就会飙升，因此布隆过滤器的长度会直接影响误判率，布隆过滤器的长度越长其误判率越小

此外，哈希函数的个数也需要权衡，哈希函数的个数越多布隆过滤器中比特位被设置为1的速度越快，但是布隆过滤器的效率越低，但如果哈希函数的个数太少，也会导致误判率变高

大佬在权衡过其中的关系后得出了一套比较得当的公式：

k 是哈希函数个数
m 为布隆过滤器长度
n为插入的元素个数
p为误判率。

我们这里可以大概估算一下，如果使用 3 个哈希函数，那么 k 的值就为 3，ln2 的值我们取 0.7，那么 m 和 n 的关系大概是 m = 4 × n ，也就是过滤器长度应该是插入元素个数的 4 倍

具体实现

因为插入过滤器的元素不仅是字符串，也可以是其他类型的数据，只有调用者能够提供对应的哈希函数将该类型的数据转换成整型即可，但一般情况下过滤器都是用来处理字符串的，我们布隆过滤器可以实现为一个模板类，所以这里可以将模板参数 K 的缺省类型设置为 string。

布隆过滤器中的成员一般也就是一个位图，我们可以在布隆过滤器这里设置一个非类型模板参数 N，用于指定位图的长度：

template<size_t N, class K = string, class Hash1 = BKDRHash, class Hash2 = APHash, class Hash3 = DJBHash>
class BloomFilter
{
public:
	//...
private:
	bitset<N> _bs;
};

实例化布隆过滤器需要调用者提供三个哈希函数，由于布隆过滤器一般处理的是字符串类型的数据，因此这里我们可以默认提供几个将字符串转换成整型的哈希函数。

这里选取将字符串转换成整型的哈希函数，是综合评分最高的 BKDRHash、APHash 和 DJBHash，这三种哈希算法在多种场景下产生哈希冲突的概率是最小的：

struct BKDRHash
{
	size_t operator()(const string& s)
	{
		size_t value = 0;
		for (auto ch : s)
		{
			value = value * 131 + ch;
		}
		return value;
	}
};
struct APHash
{
	size_t operator()(const string& s)
	{
		size_t value = 0;
		for (size_t i = 0; i < s.size(); i++)
		{
			if ((i & 1) == 0)//偶数情况
			{
				value ^= ((value << 7) ^ s[i] ^ (value >> 3));
			}
			else//奇数情况
			{
				value ^= (~((value << 11) ^ s[i] ^ (value >> 5)));
			}
		}
		return value;
	}
};
struct DJBHash
{
	size_t operator()(const string& s)
	{
		if (s.empty())
			return 0;
		size_t value = 5381;
		for (auto ch : s)
		{
			value += (value << 5) + ch;
		}
		return value;
	}
};

插入

布隆过滤器当中需要提供一个 set 接口用于插入元素，插入元素时，需要通过三个哈希函数分别计算出该元素对应的三个比特位，然后在位图中设置为1即可：

void Set(const K& key)
{
	size_t i1 = Hash1()(key) % N;
	size_t i2 = Hash2()(key) % N;
	size_t i3 = Hash3()(key) % N;

	//设置位图中三个位状态
	_bs.set(i1);
	_bs.set(i2);
	_bs.set(i3);
}

查找

布隆过滤器当中还需要提供一个 test 接口用于检测元素是否已经出现。检测时，需要通过三个哈希函数分别计算出该元素对应的三个比特位，然后判断这三个比特位是否被设置为1。

1. 只要有一个比特位未被设置则说明该元素一定不存在。
2. 如果三个比特位全部被设置，则返回 true 表示该元素存在（可能仍存在误判）

bool Test(const K& key)
{
	size_t i1 = Hash1()(key) % N;
	if (_bs.test(i1) == false)
	{
		return false; //key一定不存在
	}

	size_t i2 = Hash2()(key) % N;
	if (_bs.test(i2) == false)
	{
		return false; //key一定不存在
	}

	size_t i3 = Hash3()(key) % N;
	if (_bs.test(i3) == false)
	{
		return false; //key一定不存在
	}

	return true; //key对应的三个位都被设置，key存在（可能误判）
}

删除

布隆过滤器一般不支持删除操作，原因如下：

首先布隆过滤器判断一个元素存在时可能存在误判，此时无法保证要删除的元素确实在过滤器当中，此时将位图中对应的比特位清 0 会影响其他元素

此外，就算要删除的元素确实在布隆过滤器当中，该元素映射的多个比特位当中有些是与其他元素共用的，此时将这些比特位清 0 也会影响其他元素

当然并不是说没办法让他正常删除，结合上面我们需要两种做法：

1. 调用 test 接口确认此对象在过滤器中可能存在，再进一步遍历存储对象的文件来确认是否真正存储有；
2. 将删除操作进行解耦，保证不会影响其他的元素，我们只需要在每个比特位加一个计数器，当存在插入操作时，在计数器里面进行 ++ 操作，删除后对该位置进行 – 即可。

当然，$为什么至今过滤器都没有提供对应的删除接口呢？$其实过滤器的本来目的就是为了提高效率和节省空间，但是在确认存在时去遍历文件，文件 IO 和磁盘 IO 的时间开销是不小的，其次在每个比特位增加额外的计数器，更是让空间开销飙升到本身的好几倍。

优劣

虽然莫须有过滤器只能保证对象可能存在，我愿称之为薛定谔的过滤器，但是他的优势也绝对亮眼：

1. 不受数据量大小影响，增加和查询元素的时间复杂度为O(K)，K为哈希函数的个数，一般比较小
2. 哈希函数相互之间没有关系，方便硬件并行运算
3. 布隆过滤器不需要存储元素本身，对保密要求比较严格的场合有很大优势
4. 在能够承受一定的误判时，布隆过滤器比其他数据结构有着很大的空间优势
5. 数据量很大时也可以表示全集，其他数据结构不能
6. 使用同一组哈希函数的布隆过滤器可以进行交、并、差运算

当然缺点也不能没有：

1. 有误判率，存在假阳性即不能准确判断元素是否在集合中（补救方法：再自建一个白名单，存储可能会误判的数据）
2. 不能获取元素本身
3. 一般情况下不能从布隆过滤器中删除元素

使用场景

因为是判断可能存在，所以首要标准就是不能到影响业务逻辑

比如当我们用手机号注册账号时，系统需要判断你填入的手机号是否已经注册过，如果注册过则会提示用户注册失败，但这种情况系统不可能直接去遍历磁盘当中的用户数据，判断该手机号是否被注册过，因为磁盘IO是很慢的，这会降低用户的体验。

这种情况下就可以使用布隆过滤器，将所有注册过的手机号全部添加到布隆过滤器当中，当我们需要用手机号注册账号时，就可以直接去布隆过滤器当中进行查找：如果不存在，则说明没有被注册过，并且避免了磁盘IO。如果存在，此时再进一步访问磁盘进行复核，确认该手机号是否真的被注册过即可

大部分情况下用户用手机号注册账号时，都知道自己有没有注册过，因此在布隆过滤器就能直接搞定，此时就避免了进行磁盘IO。而只有布隆过滤器误判或用户忘记的情况下，才需要访问磁盘进行复核

aqa 芭蕾 eqe 亏内，代表着开心代表着快乐，ok 了家人们