79-七大排序总结
目录
1.辅助测试排序的性能和正确性
2.排序总代码实现
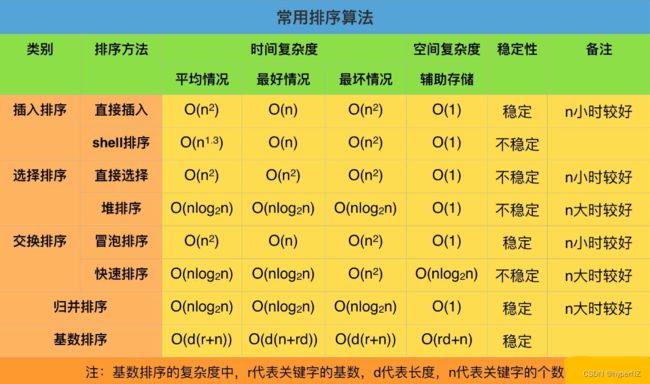
3.时间复杂度、空间复杂度、稳定性
1.辅助测试排序的性能和正确性
测试用例的选择:类似排序这种随机性比较大的问题,要多选数字,数字是随机数生成的,这种测试用例才具备代表性。
实现方法(都是一些工具方法):
- 生成n个随机数的方法。
- 生成n个近乎有序的数(测试数据敏感度)。
- 判断数组是否是升序集合(测试排序算法是否正确)。
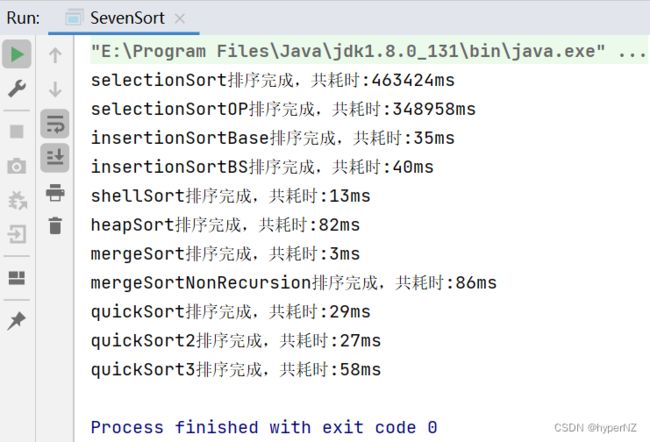
- 测试排序的性能——完全相同数据下不同算法耗时情况。
import java.lang.reflect.Method;
import java.util.Arrays;
import java.util.concurrent.ThreadLocalRandom;
/**
* 排序的辅助类
*/
public class SortHelper {
/**
* 生成随机数的一个类
* 之前的Random,(线程不安全,有可能相同的随机数被使用多次)
* 故使用:通过ThreadLocalRandom这个类的current方法来取得一个random对象,而不是直接new一个对象,
* 用法和random差不多
*/
private static final ThreadLocalRandom random = ThreadLocalRandom.current();
/**
* 1.生成一个具有n个数的随机数组,取值范围是从[L...R]
* @param n
* @param L
* @param R
* @return
*/
public static int[] generateRandomArray(int n, int L, int R) {
int[] ret = new int[n];
for(int i = 0; i < n; i ++) {
ret[i] = random.nextInt(L, R);
}
return ret;
}
/**
* 2.生成一个有n个数的近乎有序的数组
* @param n 数据个数
* @param times 交换次数
* @return
*/
public static int[] generateSortedArray (int n, int times) {
//n个完全有序的数组
int[] ret = new int[n];
for (int i = 0; i < n; i++) {
ret[i] = i;
}
//交换ret中若干个元素的位置,就会打乱其平衡
for (int i = 0; i < times; i++) {
//取任意的两个索引下标
int index1 = random.nextInt(0,n-1);
int index2 = random.nextInt(0,n-1);
swap(ret, index1, index2);
}
return ret;
}
/**
* 3.判断数组arr是否完全是升序集合,验证排序算法的正确性
* @param arr
* @return
*/
public static boolean isSorted(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
if (arr[i] > arr[i + 1]) {
System.err.println("排序算法有误");
return false;
}
}
return true;
}
/**
* 4.根据排序名称来调用相应的排序算法来对arr做排序处理
* 利用java中的反射
* @param sortName
* @param arr
*/
public static void testSort(String sortName, int[] arr) throws Exception {
//用一下反射的知识,相当于在运行的过程中动态的获取一些方法或者属性,因为在java中无法将一个方法传递给另一个方法
//因为java没有方法指针,所以通过反射来进行传入
//首先获取class对象,就是SevenSort
Class cls = SevenSort.class;
//通过反射获取方法
Method method = cls.getDeclaredMethod(sortName,int[].class);
long start = System.nanoTime();
//invoke方法,第一个参数是通过哪个对象来调用的,我们此时都是静态方法,所以不需要对象,传null就可以
//第二个参数告诉JDK方法参数是啥,我们的是整形数组,任何一个排序算法都是传入一个整形数组
//调用这个排序算法
method.invoke(null, arr);
long end = System.nanoTime();
if(isSorted(arr)) {
System.out.println(sortName + "排序完成,共耗时:" + (end - start) / 1000000 + "ms");
}
}
/**
* 5.拷贝数组
* @param arr
* @return
*/
public static int[] arrCopy(int[] arr) {
return Arrays.copyOf(arr, arr.length);
}
/**
* 6.交换三连
* @param ret
* @param index1
* @param index2
*/
private static void swap (int[] ret, int index1, int index2) {
int temp = ret[index1];
ret[index1] = ret[index2];
ret[index2] = temp;
}
} 2.排序总代码实现
import java.util.concurrent.ThreadLocalRandom;
/**
* 七大排序实现
*/
public class SevenSort {
private static final ThreadLocalRandom random = ThreadLocalRandom.current();
/**
* 直接选择排序
* @param arr
*/
//排序是一个工具,我们都用static静态方法
public static void selectionSort(int[] arr) {
//每次从待排序数组中选择最小值放在待排序数组的最前面
//最外层的for循环表示要执行的总次数,类似于冒泡,当剩下最后一趟时,整个数组已经有序
//默认第一个元素就是有序的
//已经有序的集合[0,i)
//待排序的集合[i+1,n)
//每次进行一趟排序,最小值就放在了数组的最前面,已经有序的集合元素个数 + 1
//待排序集合元素个数 - 1
for(int i = 0; i < arr.length - 1; i++) {
//min变量存储了最小值元素的下标
int min = i;
//每次从无序区间中选择最小值
for(int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
//此时min就存储了最小值的元素下标,就把min对应的元素换到无序区间的最前面
swap(arr, i, min);
}
}
/**
* 双向选择排序
* 每次选出最小值放前面,最大值放后面
* @param arr
*/
public static void selectionSortOP(int[] arr) {
int low = 0, high = arr.length - 1;
//有序区间[0, low + 1)
//用<,无序区间只剩一个元素,当low==high时,直接跳出循环,不用走下面的判断
while(low < high) {
int min = low, max = low;
for(int i = low + 1; i <= high; i++) {
if (arr[i] > arr[max]) {
max = i;
}
if(arr[i] < arr[min]) {
min = i;
}
}
//min存储了无序区间的最小值,max存储了无序区间的最大值
swap(arr, low, min);
if(max == low) {
//当max就处在low的位置,由于swap(arr,low,min),low对应的元素值修改了,修改到min对应的下标
//(相当于将min和max这俩下标对应的值交换了,其下标也要进行交换)
max = min;
}
swap(arr, max, high);
low += 1;
high -= 1;
}
}
/**
* 直接插入排序
* 每次选择无序区间的第一个元素,插入到有序区间的合适位置
* @param arr
*/
public static void insertionSortBase(int[] arr) {
//有序区间[0,i) [0,1)
//默认第一个元素就是有序
for (int i = 1; i < arr.length; i++) {
//每次选择无序区间的第一个元素,插入到有序区间的合适位置
//无序区间[i, n)
for (int j = i; j > 0 && arr[j] < arr[j - 1]; j--) {
swap(arr, j, j-1);
// //arr[j] > arr[j - 1]此时循环直接终止
// //arr[j - 1]已经是有序区间元素,大于前面的所有值
}
}
}
/**
* 折半插入排序
* @param arr
*/
public static void insertionSortBS(int[] arr) {
for (int i = 1; i < arr.length; i++) {
//无序区间第一个值
int val = arr[i];
//有序区间[0,i)
int low = 0;
int high = i;
while(low < high) {
int mid = (low + high) >> 1;
//将相等的值放在左半区间,保证稳定性
if(val >= arr[mid]) {
low = mid + 1;
}else{
//右区间取不到,不用 -1
high = mid;
}
}
//数据搬移
for (int j = i; j > low; j--) {
arr[j] = arr[j - 1];
}
//low就是元素插入位置
arr[low] = val;
}
}
/**
* 在数组arr[l...r]上使用插入排序
* @param arr
* @param l
* @param r
*/
private static void insertBase(int[] arr, int l, int r) {
//有序的区间[l...i]
//无序的区间[i...r]
for (int i = l + 1; i <= r; i++) {
for (int j = i; j > l && arr[j] < arr[j - 1]; j--) {
swap(arr, j, j - 1);
}
}
}
/**
* 希尔排序
* @param arr
*/
public static void shellSort(int[] arr) {
int gap = arr.length >> 1;
while(gap > 1) {
//不断按照Gap分组,组内按照插入排序
insertionSortGap(arr, gap);
gap /= 2;
}
//整个数组的插入排序
insertionSortGap(arr,1);
}
/**
* 按gap分组,组内按插入排序
* @param arr
* @param gap
*/
private static void insertionSortGap(int[] arr, int gap) {
//外层从gap索引处开始不断向后走到数组末尾
//i = 4
for (int i = gap; i < arr.length; i++) {
//内层从gap索引开始向前看,看的元素就是距离他gap长度的元素
//不断比较当前元素和前面gap元素的大小
//j - gap >= 0,说明前面数组还有相同距离的元素,比较arr[j] 和 arr[j - gap]的大小
//j = 9
for (int j = i; j - gap >= 0 && arr[j] < arr[j - gap] ; j = j - gap) {
swap(arr, j, j - gap);
}
}
}
/**
* 将任意数进行原地堆排序
* @param arr
*/
public static void heapSort(int[] arr) {
//将任意数组调整为最大堆,从最后一个非叶子节点开始
for (int i = (arr.length - 1 - 1) / 2; i >= 0 ; i--) {
siftDown(arr, i, arr.length);
}
//依次将堆顶元素和最后位置元素交换
//最开始:待排序数组[0...arr.length - 1],已排序数组[];
//交换第一个元素之后:待排序数组[0...arr.length - 2],已排序数组[arr.length - 1];
//交换第二个元素之后:待排序数组[0...arr.length - 3],已排序数组[arr.length - 2,arr.length - 1];
//此处终止条件不用写i = 0,当整个待排序数组就剩一个元素时,整个数组已经有序
for (int i = arr.length - 1; i >0; i--) {
swap(arr, 0, i);
siftDown(arr, 0, i);
}
}
/**
* 元素下沉操作
* @param arr
* @param i
* @param n 当前arr中有效的元素个数
*/
private static void siftDown(int[] arr, int i, int n) {
//仍然存在子树
while((2 * i + 1) < n) {
int j = 2 * i + 1;
//右孩子存在且大于左子树值
if (j + 1 < n && arr[j + 1] > arr[j]) {
j = j + 1;
}
//j对应的下标就是左右子树的最大值
if(arr[i] >= arr[j]) {
break;
} else {
swap(arr,i,j);
i = j;
}
}
}
/**
* 将任意数组进行冒泡排序
* @param arr
*/
public static void bubbleSort(int[] arr) {
//最外层表示要比较的趟数,此处-1是因为,整个待排序数组剩一个元素时,整个数组已经有序
for (int i = 0; i < arr.length - 1; i++) {
boolean isSwaped = false;
//此处-1是为了防止越界
for (int j = 0; j < arr.length - i - 1; j++) {
if(arr[j] > arr[j + 1]){
isSwaped = true;
swap(arr, j, j + 1);
}
}
if(!isSwaped){
//内层循环没有元素交换,整个数组有序
break;
}
}
}
/**
* 在arr上进行归并排序
* @param arr
*/
public static void mergeSort(int[] arr) {
mergeSortInternal(arr, 0, arr.length - 1);
}
/**
* 在arr[l...r]上进行归并排序
* @param arr
* @param l
* @param r
*/
private static void mergeSortInternal(int[] arr, int l, int r) {
//优化① 减少若干次递归的过程
if(r - l <= 15){
//拆分后的小区间直接使用插入排序,不再递归
insertBase(arr, l, r);
return;
}
// if(l >= r){
// //区间只剩下一个元素,整个区间有序,不需要再排序
// return;
// }
//若r和l都特别大的时候,有溢出的风险 (r + l) >> 1
int mid = l + ((r - l) >> 1); //会规避溢出风险
//在拆分后的两个小数组上使用归并排序
//先排序左半区间
mergeSortInternal(arr, l, mid);
//再排序右半区间
mergeSortInternal(arr, mid + 1, r);
// //此时左半区间和右半区间已经有序,只需要合并两个小区间即可
// merge(arr, l, mid, r);
//优化② 减少若干次合并的过程
//arr[mid]是左区间的最后一个元素,arr[mid + 1]是右区间的第一个元素
//不是上来就和并,当两个小区间之间存在乱序时才合并
//arr[mid] < arr[mid + 1],说明左区间已经小于右区间的所有值,整个区间已经有序,不需要merge
if(arr[mid] > arr[mid + 1]) {
merge(arr, l, mid, r);
}
}
/**
* 将已经有序的arr[l...mid]和arr[mid + 1...r]合并为一个大的有序数组arr[l...r]
* @param arr
* @param l
* @param mid
* @param r
*/
private static void merge(int[] arr, int l, int mid, int r) {
//假设此时l = 1000, r = 2000
//开辟一个大小和合并后数组大小相同的数组
int[] temp = new int[r - l + 1];
//将原数组内容拷贝到新数组中
for (int i = l; i <= r; i++) {
//temp[0] = arr[1000]
//新数组的索引和原数组的索引有l个单位的偏移量
temp[i - l] = arr[i];
}
//遍历原数组,选择左半区间和右半区间的最小值写回原数组
//i对应于左半有序区间的第一个索引
int i = l;
//j对应右半区间的第一个索引
int j = mid + 1;
//k表示当前处理到原数组的哪个位置
for (int k = l; k <=r; k++) {
if(i > mid){
//此时左半区间已经全部处理完毕,将右半区间的所有值写回原数组
arr[k] = temp[j - l];
j++;
} else if(j > r) {
//此时右半区间已经全部处理完毕
arr[k] = temp[i - l];
i++;
} else if(temp[i - l] <= temp[j - l]) {
arr[k] = temp[i - l];
i++;
} else {
arr[k] = temp[j - l];
j ++;
}
}
}
/**
* 归并排序的非递归版本
* @param arr
*/
public static void mergeSortNonRecursion(int[] arr) {
//sz表示每次合并的元素个数,最开始从1个元素开始合并,(每个数组只有一个元素)
//第二次循环时,合并的元素个数就成了2(每个数组有两个元素)
//第三次循环时,合并的元素个数就成了4(每个数组有四个元素)
for (int sz = 1; sz <= arr.length; sz = sz + sz) {
//merge过程,i表示每次merge开始的索引下标
for (int i = 0; i + sz < arr.length; i += sz + sz) {
//i + sz表示第二个小数组的开始索引 < n 表示还有右半区间要合并
//当sz长度过大时,i + 2sz - 1会超过数组长度了
merge(arr, i, i + sz - 1, Math.min(i + 2 * sz - 1, arr.length - 1) );
}
}
}
/**
* 快速排序 一路快排
* @param arr
*/
public static void quickSort(int[] arr) {
quickSortInternal(arr, 0, arr.length - 1);
}
/**
* 在l...r上进行快速排序
* @param arr
* @param l
* @param r
*/
private static void quickSortInternal(int[] arr, int l, int r) {
//递归终止时,小数组使用插入排序
if(r - l <= 15) {
insertBase(arr, l ,r);
return;
}
//选择基准值,找到该值对应的下标
int p = partition(arr, l, r);
//在<基准值区间进行快速排序
quickSortInternal(arr, l, p - 1);
//在>=基准值区间进行快速排序
quickSortInternal(arr, p + 1, r);
}
/**
* 在arr[l...r]上选择基准值,将数组划分为 = v 两部分,返回基准值对应的元素下标
* @param arr
* @param l
* @param r
* @return
*/
private static int partition(int[] arr, int l, int r) {
//优化:随机选择一个元素值作为基准值(在当前数组中)
int randomIndex = random.nextInt(l, r);
swap(arr, l, randomIndex);
int v = arr[l];
// //默认选择数组的第一个元素作为基准值
// int v = arr[l];
//arr[l + 1...j] < v
int j = l;
//i是当前处理的元素下标
//arr[l + 1...j] < v 最开始为空区间 [l + 1...l] = 0
//arr[j + 1...i] >= v 最开始为空区间 [l + 1...l + 1] = 0
for (int i = l + 1; i <= r; i++) {
if(arr[i] < v) {
swap(arr, j + 1, i);
//小于v的元素值新增一个
j++;
}
}
//此时j下标对应的就是最后一个 < v 的元素,交换j和l的值,选取的基准值交换到j的位置
swap(arr, l, j);
return j;
}
/**
* 二路快排
* @param arr
*/
public static void quickSort2(int[] arr) {
quickSortInternal2(arr, 0, arr.length - 1);
}
/**
*
* @param arr
* @param l
* @param r
*/
private static void quickSortInternal2(int[] arr, int l, int r) {
if(r - l <= 15) {
insertBase(arr, l, r);
return;
}
int p = partition2(arr, l, r);
quickSortInternal2(arr, l, p - 1);
quickSortInternal2(arr, p + 1, r);
}
/**
*
* @param arr
* @param l
* @param r
* @return
*/
private static int partition2(int[] arr, int l, int r) {
int randomIndex = random.nextInt(l, r);
swap(arr, l, randomIndex);
int v = arr[l];
//arr[l + 1...i) < v
int i = l + 1;
//arr(j...r] > v
int j = r;
while(true) {
//i从前向后扫描碰到第一个 >= v 的元素停止
while (i <= r && arr[i] < v) {
i++;
}
//j从后向前扫描,碰到第一个 <= v 的元素停止
while(j >= l + 1 && arr[j] > v) {
j--;
}
if(i > j) {
//此时整个数组已经全部扫描完毕
break;
}
swap(arr, i, j);
i++;
j--;
}
//此时j落在最后一个 <= v的元素
swap(arr, l, j);
return j;
}
/**
* 三路快排
* @param arr
*/
public static void quickSort3(int[] arr) {
quickSortInternal3(arr, 0, arr.length - 1);
}
/**
*
* @param arr
* @param l
* @param r
*/
private static void quickSortInternal3(int[] arr, int l, int r) {
if(r - l <= 15) {
insertBase(arr, l, r);
return;
}
int randomIndex = random.nextInt(l, r);
swap(arr, l, randomIndex);
int v = arr[l];
//arr[l + 1...lt] < v
int lt = l;
//arr[gt...r] > v
int gt = r + 1;
//arr[lt + 1...i) == v
int i = l + 1;
//终止条件 i == gt
while(i < gt) {
if(arr[i] < v) {
//arr[l + 1...lt] < v
swap(arr, lt + 1, i);
lt++;
i++;
}else if(arr[i] > v) {
//arr[gt...r] > v
swap(arr, gt - 1, i);
gt--;
//此时i无需++,因为gt - 1这个元素还没有处理,刚好换到了i这个位置继续处理
}else{
//arr[lt + 1...i) == v
i++;
}
}
swap(arr, l, lt);
//arr[l...lt - 1] < v
quickSortInternal3(arr, l, lt - 1);
//arr[gt...r] > v
quickSortInternal3(arr, gt, r);
}
/**
* 判断数组中元素是否有序排列(小->大)
* @param arr
* @return
*/
public static boolean isSorted(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
if(arr[i] > arr[i + 1]) {
return false;
}
}
return true;
}
/**
* 交换操作
* @param arr
* @param i
* @param j
*/
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) throws Exception {
int n = 1000000;
int[] arr = SortHelper.generateSortedArray(1000000,100);
int[] arrCopy = SortHelper.arrCopy(arr);
int[] arrCopy1 = SortHelper.arrCopy(arr);
int[] arrCopy2 = SortHelper.arrCopy(arr);
int[] arrCopy3 = SortHelper.arrCopy(arr);
SortHelper.testSort("selectionSort", arr);
SortHelper.testSort("selectionSortOP",arrCopy);
SortHelper.testSort("insertionSortBase",arrCopy1);
SortHelper.testSort("insertionSortBS",arrCopy2);
SortHelper.testSort("shellSort",arr);
SortHelper.testSort("heapSort",arrCopy);
SortHelper.testSort("mergeSort",arr);
SortHelper.testSort("mergeSortNonRecursion",arrCopy1);
SortHelper.testSort("quickSort",arrCopy);
SortHelper.testSort("quickSort2",arrCopy3);
SortHelper.testSort("quickSort3",arrCopy3);
}
}