软考 - 数据结构与算法
数据结构
线性结构
线性表
存储结构
-
顺序存储:用一组地址连续的存储单元 依次存储线性表中的数据元素,使得逻辑上相邻的元素物理上也相邻。
-
链式存储:存储各数据元素的结点的地址并不要求是连续的,数据元素逻辑上相邻,物理上分开。
例题:
若长度为n的线性表采用链式存储结构,要在第i个位置(0<=i<=n)插入一个新元素的算法的时间复杂度为(On)?
解:
一般来讲,链式存储很方便插入和删除,确实是O(1),但是这是建立在你有指针指向要插入的位置作为前提的。
本题无专门指针,强调了第i个位置,那么就还需要额外的O(n)来找到第i个位置。
栈和队列
- 循环队列的计算
串的模式匹配算法
- 基本的匹配方法
- KMP算法【掌握】
矩阵
- 特殊矩阵:对称矩阵,对角矩阵,三角矩阵
- 稀疏矩阵
树与二叉树
树的基本概念
(1)双亲、孩子和兄弟。结点的子树的根称为该结点的孩子;相应地,该结点称为其子结点的双亲。具有相同双亲的结点互为兄弟。
(2)结点的度。一个结点的子树的个数记为该结点的度。
(3)叶子结点。叶子结点也称为终端结点,指度为0的结点。
(4)内部结点。度不为0的结点,也称为分支结点或非终端结点。除根结点以外,分支结点也称为内部结点。
(5)结点的层次。根为第一层,根的孩子为第二层,依此类推,若某结点在第i层,则其孩子结点在第计1层。
(6)树的高度。一棵树的最大层数记为树的高度(或深度)。
(7)有序(无序)树。若将树中结点的各子树看成是从左到右具有次序的,即不能交换,则称该树为有序树,否则称为无序树。
例:
若n2、n1、n0分别表示一个二叉树中度为2、度为1和叶子结点的数目(结点的度定义为结点的子树数目),
则对于任何一个非空的二叉树,() 。
解:
叶子节点 = 度为2的结点+1
https://zhidao.baidu.com/question/306578964.html
- 在树中,结点总数 = 分支总数+1 【只有总结点没有分支】
二叉树【重点】
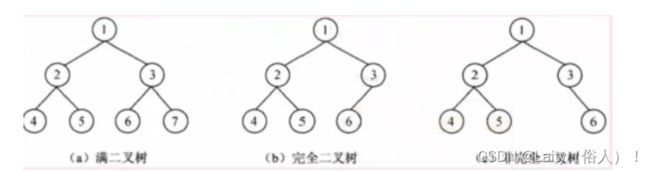
三种二叉树
完全二叉树的k-1层是满结点的,第k层结点从左到右是满的。 如下图所示:
二叉树存数结构
- 顺序存储
- 链式存储
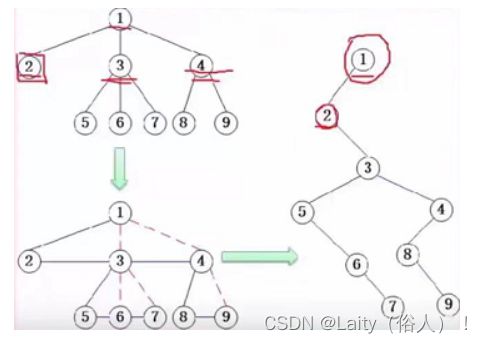
具有3个结点的二叉树有5种,可推测出具有4个节点的二叉树有()种?
如果增加的结点是根结点,则可以分为在原有结点的左侧和右侧两种情况,则有5*2=10种二叉树。如下图,虚线代表一种可能性。
上面的情况是根结点一个分支,当根结点为两个分支时,又有4种情况:
https://blog.csdn.net/Stephen___Qin/article/details/109557499
二叉树遍历
- 先序(前序)遍历:根左右
- 中序遍历:左根右
- 后续遍历:左右根
- 层次遍历:上下,左右
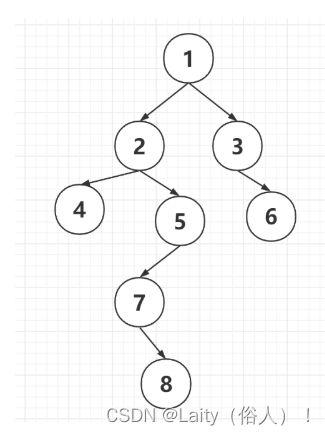
例:
前序:12457836
中序:42785136
后序;48752631
反向构造二叉树
仅仅有前序和后序是无法构造二叉树的,必须要是和中序遍历的集合才能反向构造出二叉树,
因为构造时前序和后序可以确定根结点,中序遍历用来确定根节点左子树和右子树
例题:
先序+中序 -> 后序 (可以推导根结点)
中序 + 后序 -> 前序(可以推导根结点)
先序+后序 不能构造确定的二叉树
层序 + 中序 可以构造 先序
层序+ 后序 不能构造 先序
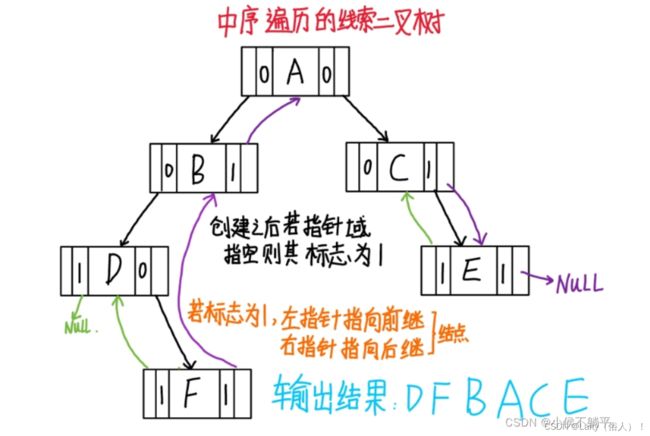
线索二叉树【重点】
笔记:https://blog.csdn.net/m0_61886762/article/details/124541056
我们现在倡导节约型社会,一切都应该以节约为本。但当我们创建二叉树时我们会发现其中一共有两个指针域,有的指针域指向的结构为空,这也就浪费了很多空间。所以为了不去浪费这些空间我们采取了一个措施。就是利用那些空地址,存放指向结点在某种遍历次序之下 的前驱和后继结点的地址。就好像GPS导航仪一样,它可以告诉我们下一站是哪里,我们是从那里来的。我们把这种指向前驱和后继的指针成为线索,加上线索的二叉链表称为线索链表,相应的二叉树就成为线索二叉树。
最优二叉树(哈夫曼树或赫夫曼树)【重点】
树的带权路径长度=所有叶子节点带权路径长度之和,即所有叶子节点的权值乘以该叶子节点所在的层次(第一层为0)之和。
权值就是指的一个节点的权重,比如把二叉树应用在编码中,权重就可以理解为码出现的概率。
- 哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
例:
若用n个权值构造一棵最优二叉树(哈夫曼树),则该二叉树的结点总数为()
解:
n 个叶子,n-1 个非叶节点,共2n-1 个。
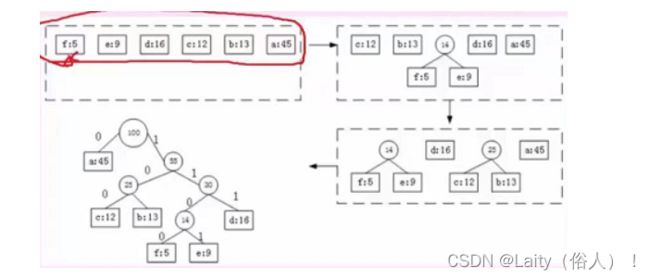
构造哈夫曼树
- 将其中两个最小的权值作为叶子节点,其和作为父节点,将其和替换两个权值,重复操作!
构造哈夫曼编码
- 构造哈夫曼树编码,左右结点相差最小,左节点小于右节点,左节点编码为0,右节点编码为1
例:采用霍夫曼编码对下列字符编码,则字符“bee”的编码为(?);编码:“110001001101”对应的字符序列为(?);
解:先画出哈夫曼树!!!
| 字符 | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| 频率(%) | 45 | 13 | 12 | 16 | 9 | 5 |
哈夫曼树的压缩比(对于二级制压缩来说)
res1 用二级制编码至少需要n位二级制,平均字符长度位n
res2 用哈夫曼树编码,平均字符长度 = n1*a1字符频率+n2*a2字符频率+n3*a3字符频率...
压缩比: (res1-res2)/res2
树和森林【不怎么考】
树的存储结构
双亲表示法:用一组连续的地址单元存储树的节点,并在每个节点中附带一个指 示器,指出其双亲节点所在数组元素的下标。
孩子表示法:在存储结构中用指针指示出节点的每个孩子,为树中每个节点的孩 子建立一个链表。
孩子兄弟表示法:又称为二叉链表表示法,为每个存储节点设置两个指针域,分 别指向该节点的第一个孩子和下一个兄弟节点。
树和森林的遍历
树和森林的遍历
由于树中每个节点可能有多个子树,因此遍历树的方法有两种:
先根遍历:先访问根节点,再依次遍历根的各颗子树。
后根遍历:先遍历根的各颗子树,再访问根节点。
森林中有很多课树,森林的遍历方法也分为两种,与树的遍历类似,就是对森林 中的每棵树都依次做先根遍历或后根遍历。
树和二叉树的转化
树的最左边结点作为二叉树的左子树,树的其他兄弟结点作为二叉树的右子树结点。
查找(排序)二叉树
一句话:中序遍历(左根右)从小到大
二叉排序树的查找效率取决于二叉排序树的深度,对于结点个数相同的二叉排序树,平衡二叉树的深度最小,而单枝树的深度是最大的,故效率最差。
二叉排序树的关键码序列
给出的序列,能够通过 左小右大 组成的查找树和给出的查找树相同!
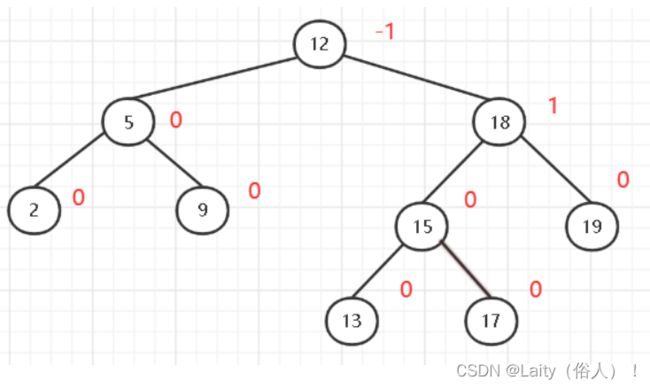
平衡二叉树
一句话:平衡二叉树就是任意左右子树层次相差不超过1
平衡二叉(AVL)树本质还是一棵二叉查找树
为了方便起见,给树上的每个结点附加一个数字,给出该结点左子树与右子树的高度差,这个数字称为结点的平衡因子(BF)
平衡因子 = 结点左子树的高度-结点右子树的高度。
因此平衡二叉树所有结点的平衡因子只能是-1、0、1,如下图,是一个平衡二叉树
图
图的种类
- 有向图
- 无向图
- 完全图:无向完全图中,节点两两之间都有连线,n个结点的连线数为n-1)+n-2+…+1 n*(-1)/2:有向完全图中,节点两两之间都有互通的两个箭头,n个节点的连线数为 n*(n-1)
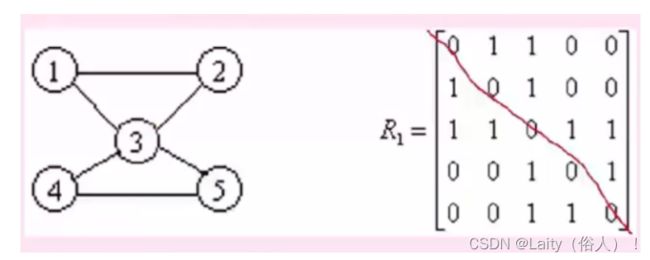
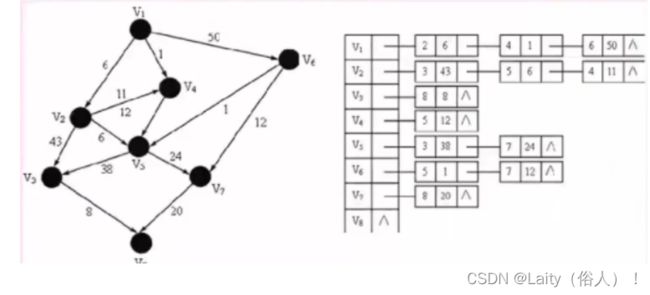
图的存储
- 临接矩阵 – 二维数组
- 临接链表 - 一维数组+链表
图的遍历
-
深度优先(dfs)
-
广度优先(bfs)
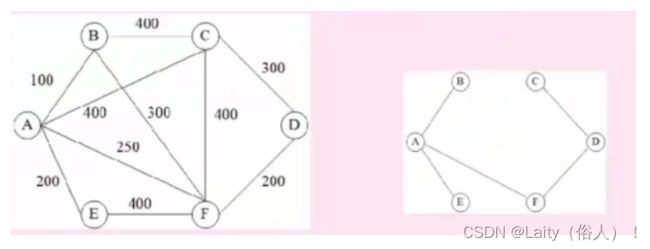
图的最小生成树【重点】
-
普利姆算法【Prim】(不断寻找最小边,然后加入集合判断)
- 适合网比较稠密
-
克鲁斯卡苏纳法【Kruscal推荐】
- 与边数相关,每次需要遍历边,适合网稀疏
- 这个算法是从边出发的,因为本质是选取权值最小的n-1条边,因此,就将边按权值大小排序,依次选取权值最小的边,直至囊括所有节点,要注意,每次选边后要检查不能形成环路。
网的拓扑序列
AV网(以顶点表示活动的网):在有向图中,以顶点表示活动,用有向边表示活 动之间的优先关系。
AV网用来表示大的工程项目执行计划,因此不能出现有向环,若存在,则意味着 某项活动必须以自身任务的完成为先决条件,因此,若要检测一个工程是否可行, 首先应检查对应的AV网是否存在回路。检测的方法是对有向图构造其顶点的拓扑 有序序列。
求拓扑序列【重点】
构造方法:将有向图的有向边作为活动开始的顺序,若图中一个节点入度为0,则 应该最先执行此活动,而后删除掉此节点和其关联的有向边,再去找图中其他没 有入度的结点,执行活动,依次进行,示例如下:

堆
构建大顶堆 和 小顶堆
算法
基础知识点
时间复杂度(渐进时间复杂度)
T(n) = 3n^3+2n^2+n 时间复杂度为 O(n^3)
时间复杂度用递归式表示的计算
- https://blog.csdn.net/qq_31829611/article/details/105063979
公式法表达式:
当参数 a、b 都确定的时候,光看递归的部分,它的时间复杂度就是:
空间复杂度
指在运行过程中 临时占用存储空间的大小(全局变量即本来就需要占用的不算)
查找
- 顺序查找
- 二分查找【重点】
(i+j)/2 - 哈希表查找
- 哈希值冲突,线性探测法,按物理地址(当前冲突地址)顺序取下一个空闲的存储空间
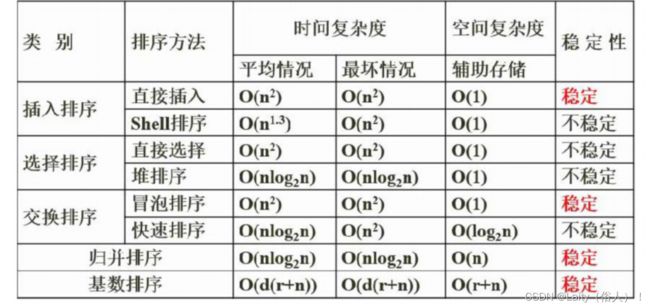
排序
稳定性:时间复杂度 和 是否改变相同数字的顺序
-
插入类排序:直接插入排序(类似玩扑克排序,从后往前比较)、希尔排序(分割若干序列直接插入排序)
-
交换类排序:冒泡排序、快速排序(二分思想,取中间值,其他值对其左右排序后,在递归)
快速排序
快速排序:
https://www.cnblogs.com/nicaicai/p/12689403.html
看源码便于理解
- 选择类排序:简单选择排序(选择最小值,只交换一次)、堆排序
- 归并排序
归并排序
- 基数排序
直接插入排序元素次数比较最小:序列为需要顺序,比较次数最小;序列为需要顺序逆序,比较次数最多!
https://blog.csdn.net/qq_44616044/article/details/115708056
搞懂直接插入排序 和 归并排序!!!
https://www.cnblogs.com/haowuji/p/6961731.html
动态规划法DP
- 构造表格,每一步最优,最后全局最优
- 求矩阵连乘??
贪心法
- 局部最优,最后全部不一定最优
KMP算法
求next函数
- https://www.jianshu.com/p/2ac684ab44c8
规定:第一个字母的 next 值置 0 (next[1] = 0),第二个字母的 next 值置 1(next[2] = 1)
从第 3 个开始,计算第 i 个位置的 next 值时,检查 p[i-1]== p[next[i-1]] ?(即这两个值是否相等)
若相等,则 next[i] = next[i-1] + 1
若不等,则继续往回找,检查p[i-1]== p[next[next[i-1]]] ?
以此类推!!
若不等,则继续往回找,直到找到下标为 1 还不等(即字符串第一个元素),直接赋值 next[i] = 1