AcWing 245. 你能回答这些问题吗（线段树）

一、题目

AcWing 246. 区间最大公约数（线段树）

二、分析

1、节点定义

我们肯定要维护是区间的左右端点。另外，根据题目的询问，我们还要去记录一下该区间的最大子段和。但是仅仅记录这三个就够了吗？

当我们无法确定我们的结构定义是否正确的时候，我们就要想一想，根据我们左右子节点中维护的数据能否更新出父节点的最大子段和？答案是不一定。

假设除了左右端点外，我们只维护了一个区间最大子段和。

假设我们的红色区间是我们父节点所代表的区间的最大子段和。那么很明显，由于这个红线所覆盖的区间也在左子节点中，所以可以直接从子节点更新过来，如果这个红线在右侧也同理。

但是还有一种情况，就是这个红线横跨两个区间。（如下图所示）

此时我们发现，父节点所代表的区间的最大子段和等于左孩子的最大后缀和加上右子树的最大前缀和。

也就是说，我们想求出当前节点的所代表区间的最大子段和，就需要再去维护子区间的最大前缀和以及最大后缀和。

好了，接下来最大子段和的问题解决了，但又衍生出了新的问题：如何维护最大的前缀和与后缀和？

我们还是去画图：

如果这个节点的最大前缀和没有超过中间点的话，那么当前节点的最大前缀和就等于左子树的最大前缀和。但是如果超过了呢？

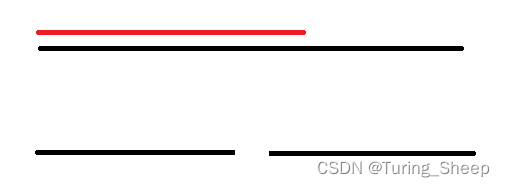
如果超过了的话，我们的最大前缀和就等于左孩子的区间和加上右孩子的最大前缀和。

所以为了及时的更新出最大前缀和与后缀和，我们还需要去维护一下区间和。

综上所述，我们的节点定义如下：

struct Node
{
	int l, r;
	int lsum;
	int rsum;
	int tsum;
	int sum;
}tre[N * 4];

2、函数分析

（1）pushup函数

这个函数的作用是利用两个子节点维护的信息去更新父节点维护的信息。函数内容即将刚刚的分析过程转化为代码即可。

void pushup(Node & u, Node & ls, Node & rs)
{
	u.sum =  ls.sum + rs.sum;
	u.lsum = max(ls.lsum, ls.sum + rs.lsum);
	u.rsum = max(rs.rsum, rs.sum + ls.rsum);
	u.tsum = max(max(ls.tsum, rs.tsum), ls.rsum + rs.lsum);
}

void pushup(int u)
{
	pushup(tre[u], tre[u << 1], tre[u << 1 | 1]);
}

（2）build函数

这个函数的作用是在一开始的时候，利用初始数组去建立我们的线段树。建树的过程只需要不断地递归即可，同时当回溯到当前状态时，说明该节点的子树都已经建好了，此时需要调用我们的$pushup$函数去利用子节点更新当前节点。

void build(int u, int l, int r)
{
	if(l == r)
	{
		tre[u] = {l, r, a[l], a[l], a[l], a[l]};
		return;
	}
	else
	{
	    tre[u] = {l, r};
		int mid = l + r >> 1;
		build(u << 1, l, mid);
		build(u << 1 | 1, mid + 1, r);
		pushup(u);
		return;
	}

}

（3）modify函数

这个函数的作用是实现题干中的单点修改操作，我们首先要递归到叶子节点，修改叶子节点后，在回溯的过程利用$pushup$来更新父节点。

void modify(int u, int x, int v)
{
	if(tre[u].l == x && tre[u].r == x)
	{
		tre[u] = {x, x, v, v, v, v};
		return;
	}
	else
	{
		int mid = tre[u].l + tre[u].r >> 1;
		if(x <= mid)
			modify(u << 1, x, v);
		else
			modify(u << 1 | 1, x, v);
		pushup(u);
	}
}

（4）query函数

假设我们查询的是下面的红色区间，那么最终我们的递归函数会查到子树中的蓝色区间。
当我们查到这些蓝色区间后，我们需要通过这些蓝色的区间维护出红色区间的答案。因此，我们可以将这些蓝色区间看作红色区间的子节点，然后通过子节点更新出当前红色区间的答案，该操作恰好就是我们的$pushup$函数。

Node query(int u, int l, int r)
{
	if(tre[u].l >= l && tre[u].r <= r)
		return tre[u];
	else
	{
		int mid = tre[u].l + tre[u].r >> 1;
		if(r <= mid)
			return query(u << 1, l, r);
		else if(l > mid)
			return query(u << 1 | 1, l, r);
		else
		{
			auto left = query(u << 1, l, r);
			auto right = query(u << 1 | 1, l, r);
			Node res;
			pushup(res, left, right);
			return res;
		}
	}
}

三、代码

#include
#define endl '\n'
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 5e5 + 10;
int a[N];
int n, m;
struct Node
{
	int l, r;
	int lsum;
	int rsum;
	int tsum;
	int sum;
}tre[N * 4];

void pushup(Node & u, Node & ls, Node & rs)
{
	u.sum =  ls.sum + rs.sum;
	u.lsum = max(ls.lsum, ls.sum + rs.lsum);
	u.rsum = max(rs.rsum, rs.sum + ls.rsum);
	u.tsum = max(max(ls.tsum, rs.tsum), ls.rsum + rs.lsum);
}

void pushup(int u)
{
	pushup(tre[u], tre[u << 1], tre[u << 1 | 1]);
}

void build(int u, int l, int r)
{
	if(l == r)
	{
		tre[u] = {l, r, a[l], a[l], a[l], a[l]};
		return;
	}
	else
	{
	    tre[u] = {l, r};
		int mid = l + r >> 1;
		build(u << 1, l, mid);
		build(u << 1 | 1, mid + 1, r);
		pushup(u);
		return;
	}

}

Node query(int u, int l, int r)
{
	if(tre[u].l >= l && tre[u].r <= r)
		return tre[u];
	else
	{
		int mid = tre[u].l + tre[u].r >> 1;
		if(r <= mid)
			return query(u << 1, l, r);
		else if(l > mid)
			return query(u << 1 | 1, l, r);
		else
		{
			auto left = query(u << 1, l, r);
			auto right = query(u << 1 | 1, l, r);
			Node res;
			pushup(res, left, right);
			return res;
		}
	}
}

void modify(int u, int x, int v)
{
	if(tre[u].l == x && tre[u].r == x)
	{
		tre[u] = {x, x, v, v, v, v};
		return;
	}
	else
	{
		int mid = tre[u].l + tre[u].r >> 1;
		if(x <= mid)
			modify(u << 1, x, v);
		else
			modify(u << 1 | 1, x, v);
		pushup(u);
	}
}

void solve()
{
	cin >> n >> m;
	for(int i = 1; i <= n; i ++ )
		cin >> a[i];
	build(1, 1, n);
	while(m --)
	{
		int opt, x, y;
		cin >> opt >> x >> y;
		if(opt == 1)
		{
		    if(x > y)
			    swap(x, y);
			cout << query(1, x, y).tsum << endl;
		}
		else
			modify(1, x, y);
	}
}

signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	solve();
}