数据结构-二叉树前中后层序遍历(顺序存储/链式存储&递归/非递归)

1 二叉树的存储与建立

1.1 顺序存储结构

1.1.1 什么是顺序存储结构

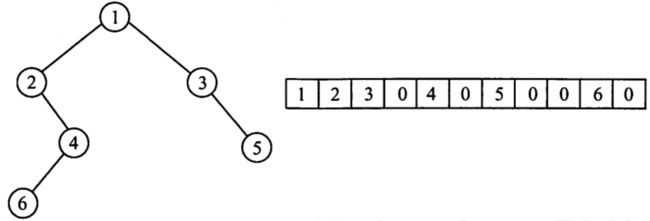
  二叉树的顺序存储结构是将二叉树中所有节点按层序遍历方式存放在一维数组中，从而实现对二叉树的存储和遍历。 如果某个节点的左子节点或右子节点为空，那么对应的数组位置就存放一个特殊的值，比如 null 或者 -1，表示该节点不存在。
比如二叉树和其顺序存储结构示意图如下：

1.1.2 代码案例

比如将上图二叉树用顺序存储结构进行存储：

#include 
#include 
#define MAX_SIZE 11

int tree[MAX_SIZE] = {0, 1, 2, 3, 0, 4, 0, 5, 0, 0, 6}; //一般从下标1开始存储，更利于后续计算

1.2 二叉链表存储

1.2.1 什么是链式存储结构

  二叉树的链式存储结构是一种常用的存储二叉树的方式，即用二叉链表进行存储。在这种存储结构中，每个节点都包含一个数据域和两个指针域，分别指向其左孩子节点和右孩子节点。整棵二叉树通过指针链接起来，形成一个链式结构。

1.2.2 代码案例

比如将上图二叉树用链式存储结构进行存储：

#include 
#include 

typedef struct node {
    int data;
    struct node *left;
    struct node *right;
} Node;

Node *createNode(int data) {
    if (data == 0) return NULL;
    Node *newNode = (Node *)malloc(sizeof(Node));
    newNode->data = data;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

int main() {
    int tree[] = {0, 1, 2, 3, 0, 4, 0, 5, 0, 0, 6, 0};
    int n = sizeof(tree) / sizeof(tree[0]);

    Node *nodes[n]; //创建了一个大小为n的指针数组nodes
    for (int i = 0; i < n; i++) {
        nodes[i] = createNode(tree[i]);
    }

    for (int i = 0; i < n; i++) {
        if (nodes[i] != NULL) {
        //假设一个节点在数组中的下标为 i (根结点编号为1)，那么它的左孩子节点和右孩子节点的下标分别为 2 * i 和 2 * i + 1
            nodes[i]->left = nodes[2 * i];
            nodes[i]->right = nodes[2 * i + 1];
        }
    }

    return 0;
}

  这段代码定义了一个 Node 结构体，表示二叉树中的一个节点。createNode 函数用于创建新的节点。在 main 函数中，创建了一个数组 tree，然后遍历这个数组，为每个非零元素创建一个节点。接着，再次遍历这个数组，根据节点在数组中的位置，将它们链接起来形成一棵二叉树。
  综上，就是用二叉链表实现了对二叉树的存储。

1.3 顺序存储结构和链式存储结构对比

二叉树顺序存储结构的优点：
访问节点快速：可以通过数组下标直接访问任意一个节点。
存储空间连续：所有节点都存储在一个连续的内存空间中，便于管理。

二叉树顺序存储结构的缺点：
空间浪费：对于不完全二叉树，数组中会有很多空位，造成空间浪费。
插入和删除操作困难：需要移动大量元素来保持树的结构。

二叉树链式存储结构的优点：
空间利用率高：每个节点都只占用实际需要的空间，不会造成空间浪费。
插入和删除操作简单：只需要修改指针即可完成插入和删除操作。

二叉树链式存储结构的缺点：
访问节点慢：需要遍历链表才能访问到指定的节点。

  总之，二叉树顺序存储结构适用于完全二叉树和满二叉树或节点数量较少的情况，而二叉树链式存储结构适用于不完全二叉树或节点数量较多的情况。

1.4 补充知识

① 含有n个结点的二叉链表中，含有n+1个空链域
② 假设一个节点在数组中的下标为 i (根结点编号为1)，那么它的左孩子节点和右孩子节点的下标分别为 2 * i 和 2 * i + 1

2 二叉树的遍历

2.1 递归算法

以下图为例

2.1.1 顺序存储结构

#include 
#define MAXSIZE 100

int tree[MAXSIZE] = {0, 1, 2, 3, 0, 4, 0, 5, 0, 0, 6};

void preOrder(int index) {
    if (tree[index] == 0 || index >= MAXSIZE) return;
    printf("%d ", tree[index]);  //根
    preOrder(index * 2);	//左
    preOrder(index * 2 + 1);  //右
}

void inOrder(int index) {
    if (tree[index] == 0 || index >= MAXSIZE) return;
    inOrder(index * 2);  //左
    printf("%d ", tree[index]); //根
    inOrder(index * 2 + 1); //右
}

void postOrder(int index) {
    if (tree[index] == 0 || index >= MAXSIZE) return; 
    postOrder(index * 2); //左
    postOrder(index * 2 + 1);  //右
    printf("%d ", tree[index]);  //根
}

void levelOrder() {
    for (int i = 1; i < MAXSIZE; i++) {
        if (tree[i] != 0) printf("%d ", tree[i]);  //层序遍历直接依次输出数组各个元素即可
    }
}

int main() {
    printf("前序遍历: ");
    preOrder(1);
    printf("\n中序遍历: ");
    inOrder(1);
    printf("\n后序遍历: ");
    postOrder(1);
    printf("\n层序遍历: ");
    levelOrder();
}

这段代码的输出结果为:

前序遍历: 1 2 4 6 3 5 
中序遍历: 2 6 4 1 3 5
后序遍历: 6 4 2 5 3 1
层序遍历: 1 2 3 4 5 6

2.1.2 链式存储结构

#include 
#include 

#define MAXSIZE 100

typedef struct BiTNode {
    int data;
    struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

//递归创建二叉树，注意是使用二级指针创建二叉树
void CreateBiTree(BiTree *T, int *a, int i) {
    if (a[i] == 0 || i > MAXSIZE) {
        *T = NULL;
    } else {
        *T = (BiTree)malloc(sizeof(BiTNode));
        (*T)->data = a[i];
        CreateBiTree(&(*T)->lchild, a, 2 * i);
        CreateBiTree(&(*T)->rchild, a, 2 * i + 1);
    }
}

void PreOrderTraverse(BiTree T) {
    if (T == NULL) {
        return;
    }
    printf("%d ", T->data);  //根
    PreOrderTraverse(T->lchild);  //左
    PreOrderTraverse(T->rchild); //右
}

void InOrderTraverse(BiTree T) {
    if (T == NULL) {
        return;
    }
    InOrderTraverse(T->lchild); //左
    printf("%d ", T->data); //根
    InOrderTraverse(T->rchild); //右
}

void PostOrderTraverse(BiTree T) {
    if (T == NULL) {
        return;
    }
    PostOrderTraverse(T->lchild); //左
    PostOrderTraverse(T->rchild); //右
    printf("%d ", T->data); //根
}

//层序一般使用队列进行辅助
void LevelOrderTraverse(BiTree T) {
    BiTree queue[MAXSIZE];
    int front = 0, rear = 0;
    BiTree p;
    if (T != NULL) {
        queue[rear++] = T;
        while (front != rear) {
            p = queue[front++];
            printf("%d ", p->data);
            if (p->lchild != NULL) {
                queue[rear++] = p->lchild;
            }
            if (p->rchild != NULL) {
                queue[rear++] = p->rchild;
            }
        }
    }
}

int main() {
    int a[MAXSIZE] = {0, 1, 2, 3, 0, 4, 0, 5, 0, 0, 6};
    BiTree T;
    CreateBiTree(&T, a, 1);

    printf("前序遍历: ");
    PreOrderTraverse(T);
    printf("\n");

    printf("中序遍历: ");
    InOrderTraverse(T);
    printf("\n");

    printf("后序遍历: ");
    PostOrderTraverse(T);
    printf("\n");

    printf("层序遍历: ");
    LevelOrderTraverse(T);
    printf("\n");

    return 0;
}

这段代码的输出结果为:

前序遍历: 1 2 4 6 3 5 
中序遍历: 2 6 4 1 3 5
后序遍历: 6 4 2 5 3 1
层序遍历: 1 2 3 4 5 6

2.2 非递归算法

我们在链式存储结构的基础上来实现代码

#include 
#include 

#define MAXSIZE 100

typedef struct BiTNode {
	int data;
	struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

//递归建立二叉树
void CreateBiTree(BiTree *T, int *a, int i) {
	if (a[i] == 0 || i > MAXSIZE) {
		*T = NULL;
	} else {
		*T = (BiTree)malloc(sizeof(BiTNode));
		(*T)->data = a[i];
		CreateBiTree(&(*T)->lchild, a, 2 * i);
		CreateBiTree(&(*T)->rchild, a, 2 * i + 1);
	}
}

void PreOrderTraverse(BiTree T) {
	BiTree stack[MAXSIZE];
	int top = -1;
	BiTree p = T;
	while (p || top != -1) {
		while (p) {
			printf("%d ", p->data);
			stack[++top] = p;
			p = p->lchild;
		}
		if (top != -1) {
			p = stack[top--];
			p = p->rchild;
		}
	}
}

void InOrderTraverse(BiTree T) {
	BiTree stack[MAXSIZE];
	int top = -1;
	BiTree p = T;
	while (p || top != -1) {
		while (p) {
			stack[++top] = p;
			p = p->lchild;
		}
		if (top != -1) {
			p = stack[top--];
			printf("%d ", p->data);
			p = p->rchild;
		}
	}
}

void PostOrderTraverse(BiTree T) {
	BiTree stack[MAXSIZE];
	int top = -1;
	BiTree p = T;
	BiTree r = NULL;
	while (p || top != -1) {
		if (p) {
			stack[++top] = p;
			p = p->lchild;
		} else {
			p = stack[top];
			if (p->rchild && p->rchild != r) {
				p = p->rchild;
				stack[++top] = p;
				p = p->lchild;
			} else {
				p = stack[top--];
				printf("%d ", p->data);
				r = p;
				p = NULL;
			}
		}
	}
}


int main() {
	int a[MAXSIZE] = {0, 1, 2, 3, 0, 4, 0, 5, 0, 0, 6};
	BiTree T;
	CreateBiTree(&T, a, 1);
	
	printf("前序遍历: ");
	PreOrderTraverse(T);
	printf("\n");
	
	printf("中序遍历: ");
	InOrderTraverse(T);
	printf("\n");
	
	printf("后序遍历: ");
	PostOrderTraverse(T);
	printf("\n");
	
	return 0;
}

2.2.1 可能的疑难点

1、为什么CreateBiTree(BiTree *T, int *a, int i)中要定义成BiTree *T而不是BiTree T?

  跟以下代码一个道理：

void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

int main() {
    int x = 1, y = 2;
    swap(&x, &y);
    printf("x = %d, y = %d\n", x, y);
    return 0;
}

  对于上述例子，简单来说，你想在函数内部对树进行修改，那么就得对指针类型进行修改，这样才能把修改后的结果带出函数外部。
  现在我们回到原代码，在CreateBiTree(&T, a, 1);中，T是指向结构体BiNode的指针，我们在CreateBiTree方法中创建二叉树，为了让修改的结果带出去，所以就需要定义BiTree *T这一个二级指针，才能修改指向结构体的指针T。然后我们才得以在PreOrderTraverse(T);InOrderTraverse(T);···一系列方法中传入T，来进行遍历。
  如果定义成BiTree T，相当于只是对形参进行操作，就不能实现对二叉树的修改创建了，简单来说也就是函数内的操作传不出去，无法传递给T，那么T没被修改，就不能继续下面的遍历工作了。

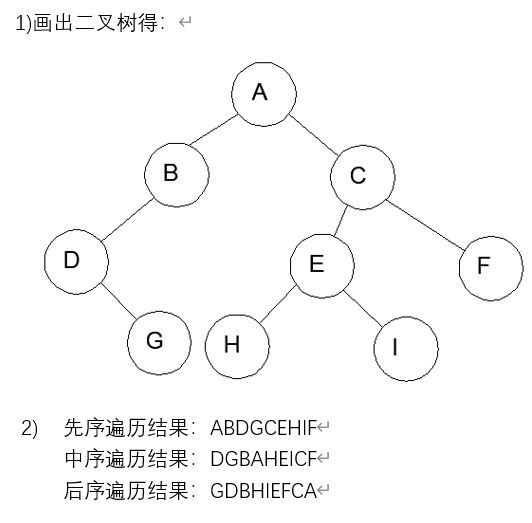
3 考研真题举例

1、




解析

2、



解析

3、



解析

4、



解析

附送一张壁纸ヽ(^ｰ^)人(^ｰ^)ノ