Dijkstra 单源最短路径算法 Java实现

算法导入

在图论中，求最短路径有一个经典的算法 Dijkstra算法（银行家算法其实也是这人提出的），就离谱。

如果已经忘了，出门右拐——银行家算法

Dijkstra（/ˈdikstrɑ/或/ˈdɛikstrɑ/）算法由荷兰计算机科学家 E. W. Dijkstra 于 1956 年发现，1959 年公开发表，是一种求解 非负权图 上单源最短路径的算法。

上面一段话有两点需要注意：1. 非负权图。指所有路径的权值都非负。2. 单源。指从一个源点到其他点的最短路径。
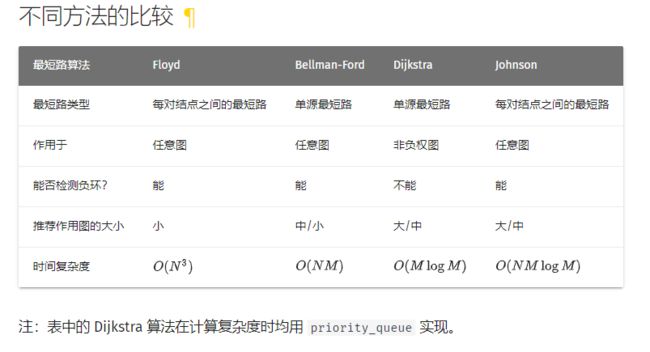
那有人想问了，求每对结点之间的最短路径，用啥呢？Floyd算法、Johnson算法。

那对于负权图，上面的算法能用吗？能用，你还能用 Bellman-Ford算法。

那，我说停停。

好，言归正传。咱们这节先介绍 Dijkstra算法，为后面的几种算法铺个路。正式开始前先告知一些图论中的定义：

• n ，图上点的数目， m 图上边的数目。
• s： 为最短路的源点。
• dis(u) ：源点 s 到 u 点的最短路长度。
• w(u,v) ：边(u, v) 的权值。

算法核心

Dijkstra算法的思想为 贪心，每次选择最短路长度最小的点，来更新相连边的最短路。从局部最优到全局最优。

初始化：

将结点分为两个集合：已确定最短路点集合 S 和 待确定最短路点集合 T。初始时，所有点都在 T 中。
初始化 dis(s) = 0，其余点的 dis 均为 正无穷。

重复操作：

1. 从T集合中，选取一个最短路长度最小的结点，移到S集合中。
2. 对刚加入S集合的所有出边，执行松弛操作。

直到T集合为空，算法结束。可能有读者不理解松弛操作是啥，公式解答如下：
对于边 (u,v) 松弛操作为： dis(v) = min(dis(v) , dis(u) + w(u,v) )

你在的城市只能坐绿皮火车去北京，哎呀老远了，要1天才能到达。突然你发现去省会只要2小时，省会坐飞机去北京只要5小时，合计7个小时，这不更香了？那肯定赶紧更新这个最短路径。

复杂度分析

判断一个算法的优劣，我们需要对算法进行复杂度分析。复杂度分析从两个维度来评判，一个是时间，一个是空间。因此，这部分我们将对Dijkstra算法进行复杂度分析。

时间复杂度

算法核心操作：

1. 从T集合中，选取一个最短路长度最小的结点，移到S集合中。
2. 对刚加入S集合的所有出边，执行松弛操作。

对于2来说，我们只需要 O(1) 的时间复杂度，重点在于如何维护最短路长度最小的结点。

• 暴力：枚举才是永远滴神。每次操作2结束后。直接在T集合中暴力寻找最短的点，需要O(n)，进行 n 次循环。总时间复杂度为 O(n^2)；2 操作对于边做处理，时间复杂度为O(m)。全过程的时间复杂度为 O(n^2 + m) = O(n^2) 。
• 二叉堆：每成功松弛一条边(u, v)，就将 v 插入二叉堆中如果v已经在二叉堆中，直接修改相应的元素的权值即可，1操作直接取堆顶结点。共计O(m)次二叉堆上的插入（修改操作），O(n) 次 删除堆顶操作，而插入和删除元素的时间复杂度为O(logn) ，时间复杂度为 O((n + m) logn)。
• 优先队列：和二叉树类似，但使用优先队列时，如果同一个点的最短路被更新多次，因为先前更新时插入的元素不能被删除，也不能被修改，只能留在优先队列中，故优先队列内的元素个数是O(m) 的，时间复杂度为 O(mlogm)。
• Fibonacci堆、线段树方式，这里咱不考虑。有兴趣同学可以自行研究。

在稀疏图中，m = O(n)，使用二叉堆实现的 Dijkstra 算法较 Bellman-Ford 算法具有较大的效率优势；而在稠密图中，这时候使用暴力做法较二叉堆实现更优。

空间复杂度

空间复杂度的主要消耗在于图的存储方式。

• 邻接矩阵：空间复杂度为 O(n^2)，消耗二维数组的空间。
• 邻接表：空间复杂度为 O(m)。因为存储的是边信息。

注：该部分参考 OI Wiki，详见：oi wiki

代码实现

由于图不同的存储方式，复杂度也不同，这里只提供较为普遍使用的两种存图方式。

针对稀疏图 m ≈ n，邻接表存图，优先队列维护最短路长度最小的结点。

import java.util.*;

/**
 * @author LKQ
 * @date 2022/4/21 16:20
 * @description Dijkstra算法：一种求解 非负权图上 单源最短路径算法，流程有两步：
 * 将结点分成两个集合：已确定最短路长度的点集（记为 S 集合）的和未确定最短路长度的点集（记为 T 集合）。一开始所有的点都属于 T 集合。
 * 定义：n 为 图上点的数目，m 为 图上边的数目
 * s 为最短路的源点
 * D(u) 为 s点到 u点的实际最短路长度，dis(u)为 s -> u 点的 估计最短路长度，
 * w(u,v)为 (u, v)这一条边的边权值。
 * 初始化 dis(s) = 0，其他点的 dis 均为 +∞。
 * 

 * 然后重复这些操作：
 * 

 * 1. 从 T 集合中，选取一个最短路长度最小的结点，移到 S集合中。
 * 2. 对那些刚刚被加入 S 集合的结点的所有出边执行松弛操作。
 * 直到 T 集合为空，算法结束。
 * 

 * 针对稠密网，当 边数量 接近点数量的平方时，采用邻接矩阵存图，枚举算法进行更好
 * 针对稀疏网，当 边数量接近点的数量时，采用邻接表存图，优先队列实现Dijkstra更好
 */
public class Solution {
    /**
     * 邻接表存储图
     */
    List<int[]>[] graph;

    /**
     * 源点到其他点的最短距离，dis[s] = 0, 其他为 +∞
     */
    int[] dis;

    /**
     * 结点 0 - n-1 是否访问
     */
    boolean[] vis;

    /**
     * 正无穷，除2的意义在于 距离相加时不会溢出int
     */
    public static final int INF = Integer.MAX_VALUE / 2;
    /**
     * 算法
     *
     * @param n    n个结点
     * @param edge 有向边 + 权值，如[1, 2, 5]表示 结点 1->2 的边权值为 5
     * @param s    源点 0 <= s < n
     */
    public void dijkstra(int n, int[][] edge, int s) {
        // 1. 抽象化。根据edge信息建图。
        // 注意：有时候edge并不会直接给出，比如一些题目给出的是字符串表示的结点，那么需要使用 Map 来 给字符串编号，再抽象化
        graph = new List[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] e : edge) {
            // w(e[0], e[1]) = e[2] 
            graph[e[0]].add(new int[]{e[1], e[2]});
        }
        // 2. 初始化源点到其他点的最短距离
        dis = new int[n];
        Arrays.fill(dis, INF);
        // 源点到自身的距离为0
        dis[s] = 0;

        // 3. 初始化访问标志，默认为false
        vis = new boolean[n];

        // 4. 初始化优先队列, 根据权值升序排序
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[1] - b[1]);
        pq.add(new int[]{s, 0});

        // 5. dijkstra
        while (!pq.isEmpty()) {
            // 弹出最短路长度最小的点 和 其权值
            int[] temp = pq.poll();
            int u = temp[0];
            // 访问过，跳过
            if (vis[u]) {
                continue;
            }
            vis[u] = true;
            // 遍历所有 u 能够到达的点，刚开始为 u = s
            for (int[] q: graph[u]) {
                // 下一个点 v, 即其边权值 w
                int v = q[0], w = q[1];
                if (dis[v] > dis[u] + w) {
                    // s->v 的距离 > s->u 的距离 + u->v 的距离，更新最短距离，注意时 s-> 其他点 距离为 +∞
                    dis[v] = dis[u] + w;
                    // 加入优先队列，s->v 的距离 dis[v]
                    pq.add(new int[]{v, dis[v]});
                }
            }
        }
    }
}

针对稠密图m ≈ n^2，采用邻接矩阵存储

import java.util.*;

/**
 * @author LKQ
 * @date 2022/4/21 20:20
 * @description 当边的数量接近点的数量，用邻接矩阵存储图，
 */
public class Solution2 {
    /**
     * 邻接矩阵存储图
     */
    int[][] graph;
    /**
     * 判断是否访问过
     */
    boolean[] vis;

    /**
     * 源点到其他点的最短距离，dis[s] = 0, 其他为 +∞
     */
    int[] dis;
    /**
     * 无穷大
     */
    int INF = Integer.MAX_VALUE / 2;

    /**
     * @param n n个结点，编号 0 .. n-1
     * @param s 源点
     * @param edges 边信息
     */
    public void dijkstra(int n, int s, int[][] edges) {
        // 1. 初始化邻接矩阵
        graph = new int[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(graph[i], INF);
            // 点到自身的权值为0
            graph[i][i] = 0;
        }
        for (int[] e : edges) {
            graph[e[0]][e[1]] = e[2];
        }
        // 2. 初始化源点到其他点的距离
        dis = new int[n];
        Arrays.fill(dis, INF);
        // 源点到自身的距离为0
        dis[s] = 0;

        // 3. 初始化访问标志
        vis = new boolean[n];

        // 4. 迭代n次
        for (int i = 0; i < n; i++) {
            // 每次找到[最短距离最小] 且 [没有更新] 点 t
            int u = 0, min = INF;
            for (int j = 0; j < n; j++) {
                if (!vis[j] && dis[j] < min) {
                    u = j;
                    min = dis[j];
                }
            }
            vis[u] = true;
            // 用点u的[最小距离]更新其他点
            for (int j = 0; j < n; j++) {
                if (dis[u] + graph[u][j] < dis[j]) {
                    dis[j] = dis[u] + graph[u][j];
                }
            }
        }
    }
}

参考资料

OI Wiki
图灵程序设计丛书 算法 第4版

结尾

如果有天兜兜转转再一次相遇 我一定会不顾一切紧紧抱着你
许嵩 《庞贝》