Direct3D 12——灯光——镜面光照
反射的发生是根据一种名为菲涅耳效应(Fresnel effect,也译作菲涅 尔效应)的物理现象。当光线到达两种不同折射率(index of refraction )介质之间的界面时,一部分光将 被反射,而剩下的光则发生折射(refract),折射率是一种介质的物理性质,即 光在真空中传播的速度与光在给定介质内的传播速度之比。我们将第二种光的反射过程称为镜面反射 (specular reflection ),把被反射的光称为镜面(反射)光(specular light)
 (a)具有法线 n 的完全光滑平整的镜面(即理想镜面)所呈现的菲涅耳效应。入射光 I 抵达表面后分为
(a)具有法线 n 的完全光滑平整的镜面(即理想镜面)所呈现的菲涅耳效应。入射光 I 抵达表面后分为
两个部分进行传播,一部分按反射方向 r 发生反射,剩余部分则以折射方向 t 折射入介质。所有这些
向量都位于同一平面内。反射向量 r 与法线 n 之间的夹角总保持为θi,而且光向量L= -I与法线 n 之间
的夹角也同为θi。至于折射向量 t 与 -n 之间的夹角则取决于两种介质间的折射率以及斯涅尔折射
定律(SnelFsLaw) (b)事实上,大多数的物体并不是完全光滑平整的理想镜面,而是在微观上
具有一定的粗糙度。这就导致了反射光与折射光分别关于反射向量与折射向量产生一些扩散
菲涅耳效应
**菲涅耳方程(Fresnelequations)**以数学方法描述了入射光线被反射的百分比, 即0≤ RF≤ 1。根据能量守恒定律,如果RF是反射光量,则(1 -RF)为折射光量。RF的值是一个RGB向量, 因为光的颜色反映了反射光量。反射的光量既依赖于介质(某些材质的反射率相对更大),也与法向量 n 与光向量 L 之间的夹角θi有关。由于光照过程的复杂性,我们一般不会将完整的菲涅耳方程用于实时渲染,而是采用石里克近似 (Schlick approximation )法来加以代替:
![]()
可以将菲涅耳效应简洁地概括为:反射光量取决于材质(RF(0°))以及法线与光向量之间的夹角。
金属会吸收透射光(transmitted light) [Mdller08],这意味着它们不具有本体反射率(body reflectance, 也有译作体反射,或体漫反射等)。虽然如此,但金属并不会看上去表现为纯黑色,因为它们的RF(0°))值 较高,也就是说,就算是在接近于0。这样的极小入射角度上,它们也能反射可观的镜面光量
表面粗糙度
真实世界中的反射物体往往不是理想镜面(perfectmirror)。尽管一个物体的表面看起来似乎十分平 滑,但从微观水平上看,它还是具有一定的粗糙度(roughness )0,如图所示,我们可以认为理想镜 面的粗糙度为0,它的微观表面法线(micro-normal,或作微表面法线)都与宏观表面法线(macro-normal, 或作宏表面法线)的方向相同。随着粗糙度的增加,微观表面法线的方向开始纷纷偏离宏观表面法线, 由此反射光逐渐扩展为一个镜面瓣(specular lobe )
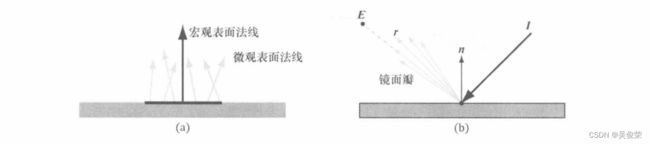
图a中,黑色的水平线条表示被放大的小面元(small surface element )。从微观角度来看,由于在此层级的表面上具有一定的粗糙度,因此许多微观表面法线各指向不同的方向。若表面愈平滑, 便会有更多的微观表面法线愈发平行于宏观表面法线;而表面越粗糙,则会有更多的微观表面法线 越发偏离于宏观表面法线。图b中,粗糙度令镜面反射光扩散开来,镜面反射光的范围称为镜面瓣。
一般来讲,镜面瓣的形状将根据建模所用的表面材质种类而各不相同
以h为法线,光从L反射至卩的微平面
为了用数学方法对粗糙度进行建模,我们采用了微平面(microfacet,也作微表面)模型。在此模型
中,我们将微观表面模拟为由多个既微小又平滑的微平面所构成 的集合;而微观表面法线正是这些微平面上的法线。针对指定的 观察单位向量 v 以及光向量L,我们需要了解由L向 v反射的所有 微平面片段的分布情况;换言之,即法线为 **h=normalize(L+v)**这种微平面片段在所有微平面中所占比例,如图所示。这样 一来,就可以确定有多少光通过镜面反射的方式,以此路径进入 到观察者的眼中一发生由L到v反射过程的微平面越多,则观 察者在此角度上看到的镜面光越明亮。
由于向量人位列向量A与向量y间的中间位置,故称之为中间向量(halfway vector,也有译作中途 向量、半角向量等)。此外,还要再引进一个中间向量方与宏观表面法线”之间的夹角θh
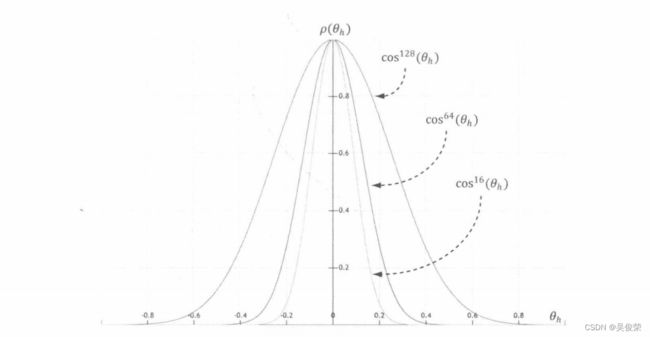
我们定义归一化分布函数p(θh)∈[0, 1],用来表示微观表面法线h与宏观表面法线n之间夹角为θh的微平面的分布情况。从直观上来讲,我们希望函数p(θh)在θh=0° 时取得最大值。也就是说,我们希 望微平面法线都平行于宏观表面法线。并盼望随着θh的增加(即渐渐偏离于宏观表面法线的微观表面法 线h),这些以向量h为法线的微平面片段逐渐减少。用来模拟以上讨论中期望模型p(θh)的一种较流行 的可控函数为:
注意到,为了求出cos(θh)=(n·h)就需要知道两种向量以及单位长度。图展示了对于取不同m 值时函数 p(θh)=cosᵐ(θh)的图像。其中,变量m控制的是粗糙度,它指定了所有以微观表面法线h与 宏观表面法线n之间夹角为θh的微平面片段。随着m的减小,表面变得更加粗糙,而微平面的法线也 都愈加偏离宏观表面法线。随着m的增大,表面变得更加光滑,微平面法线也都越发趋于宏观表面法线。
我们可以将以 p(θh) 与某种归一化因子进行组合,从而获得基于粗糙度来模拟镜像反射光量的新函数:

图展示了此函数根据不同取值的变量m所得到的图像。与之前一样,变量m依然控制着粗糙 度,但是我们还为之加上了归一化因子 m+8/8,以使光能守恒。该归一化因子实际上支配着图中曲线的高度,因此随着变量m的变化使镜面瓣变宽或变窄,令光能整体达到守恒。对于较小的m值来说, 表面会更加粗糙,并且镜面瓣变宽,继而促使光能散播得更广。因此,我们预计镜面高光(specular highlight,即镜面光)会变暗,因为其能量已经被广泛播散岀去了。另一方面,对于较大的m值而言, 表面会更加平滑,而镜面瓣会变得更窄。因此,我们预计镜面高光会更亮,因为其能量更为集中。从几 何角度上来看,变量m控制着镜面瓣的扩散程度。如果要模拟光滑的表面(例如被抛光的金属)就使用 较大的m值,而针对更粗糙的表面而言,则使用较小的m值。
我们把菲涅耳反射以及表面粗糙度这两个公式的组合来作为这一节的尾声。首先尝试计算在观察方 向v上所反射的光量。回顾以h为法线,且反射光沿观察向量v传播的微平面。设αh为光向量v与中间向量h之间的夹角,那么,根据菲涅耳效应所言,RF(αh)反映了关于h射入v的反射光 量。又由于表面的粗糙度为S(θh),所以我们还要将反射光量RF(αh乘以粗糙度。由此,我们便可得到 镜面反射光量:设(max(L· n, 0) (BL)表示入射光照到表面上一点的光量,而根据粗糙度与菲涅耳效应,(max(L· n, 0) (BL)这一段镜面反射到观察者眼中的实际光量为:
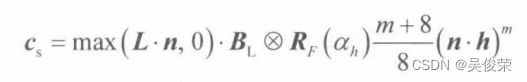
可以发现,如果L・n ≤ 0,那么所计算的结果是射向表面另一侧的光,因而此时的正表面并不会接 收到任何光照。