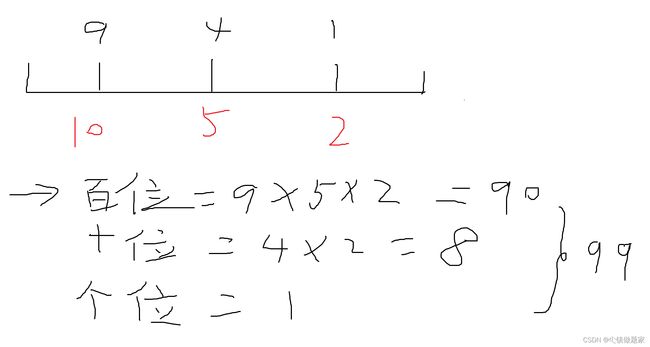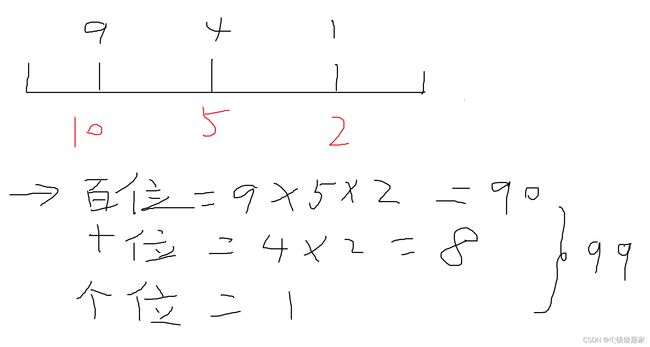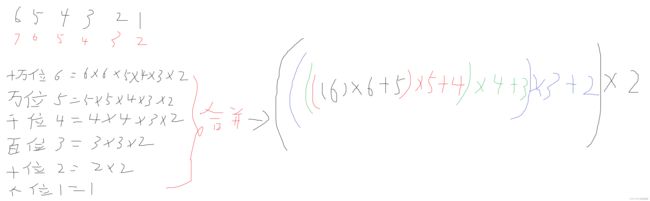蓝桥杯：X进制减法

蓝桥杯：X进制减法https://www.lanqiao.cn/problems/2108/learning/

目录

问题描述

输入格式

输出格式

样例输入

样例输出

样例说明

评测用例规模与约定

题目分析(贪心)

        X进制转换推导：

        解题：

AC代码(Java):

---

问题描述

        进制规定了数字在数位上逢几进一。

        X 进制是一种很神奇的进制, 因为其每一数位的进制并不固定！例如说某 种 X 进制数, 最低数位为二进制, 第二数位为十进制, 第三数位为八进制, 则 X 进制数 321 转换为十进制数为 65 。

        现在有两个 X 进制表示的整数 A 和 B, 但是其具体每一数位的进制还不确 定, 只知道 A 和 B 是同一进制规则, 且每一数位最高为 N 进制, 最低为二进 制。请你算出 A−B 的结果最小可能是多少。

        请注意, 你需要保证 A 和 B 在 X 进制下都是合法的, 即每一数位上的数字要小于其进制。

输入格式

        第一行一个正整数 N, 含义如题面所述。

        第二行一个正整数 Ma​, 表示 X 进制数 A 的位数。

        第三行 Ma​ 个用空格分开的整数, 表示 X 进制数 A 按从高位到低位顺序各 个数位上的数字在十进制下的表示。

        第四行一个正整数 Mb​, 表示 X 进制数 B 的位数。

        第五行 Mb​ 个用空格分开的整数, 表示 X 进制数 B 按从高位到低位顺序各 个数位上的数字在十进制下的表示。

        请注意, 输入中的所有数字都是十进制的。

输出格式

        输出一行一个整数, 表示 X 进制数 A−B 的结果的最小可能值转换为十进制后

        再模 1000000007 的结果。

样例输入

11
3
10 4 0
3
1 2 0

样例输出

94

样例说明

        当进制为: 最低位 2 进制, 第二数位 5 进制, 第三数位 11 进制时, 减法 得到的差最小。此时 A 在十进制下是 108,B 在十进制下是 14 , 差值是 94。

评测用例规模与约定

对于 30%30% 的数据, N≤10;Ma​,Mb​≤8.

对于 100%100% 的数据,2≤N≤;1≤Ma​,Mb​≤; A≥B.

题目分析(贪心)

        X进制转换推导：

        首先这道题我们要明白进制之间推导的过程。

        拿4进制来说，我们来让4进制的321转换成10进制。

        首先是个位的1，因为只有自身，所以肯定是1

        然后是十位的2，根据进制公式是

        然后是百位的3，根据进制公式是

        为什么十位到百位会从呢？因为个位只有满4了，才会向百位进1，也就是百位上一个1，就对应十位上的4.

        与之相同，一个十位上的1，就相当于一个个位上的4。

        也就是说，一个百位上的1，等于4个十位上的4，等于4*4个个位上的1.

        这就是进制之间转换的规律，也就是进制每一位是对应进制的N-1次方的由来。

---

        然后我们继续分析题目X进制的321，结果是65.

        题目已经给出了，最低位是1，第二位是10，第三位是8，那么我们画个图记录一下进制关系

        其中第一行代表是数字，第二行是对应位置代表的进制，然后我们开始计算一下：

 

        看不懂图没关系，我们一个个来分析，可以随时根据图片来继续对比。

        首先是个位1，这个他的后面没有位数了，所以它就是1

        然后是十位2，我们不能直接按照10进制的方式来进行计算，我们要从后面的位数推导上来。

        也就是十位的2，是需要从后面的位数，也就是个位推导出来的，我们已经知道个位是2进制了，那么如果十位要为1的话，也就是个位需要2个数，才会在二进制的情况下，转换成十位的1。如：2，这个数是用二进制表示就是 10。因此十位是1，代表需要2个数。

        但是十位是2，也就是说，需要4个数，个位2个数=十位1个数，我们十位这里是2，所以需要的是个位的4个数，因此十位的计算是 .

        再到百位：百位是3，那么我们从后面一位，也就是十位来推到，十位是10进制，也就是如果百位是1的话，那么就需要十位的10个数。

        所以百位是3，那么就需要十位的30个数，之前我们推到过了，十位的1个数，需要个位的2个数，因此百位的3一共需要个数。

        因此百位，十位，个位加起来一共就是60+4+1 = 65。1个 个位的数对应 1个十进制的1。

        接下来再看样例里面的X进制转换成十进制：

         继续按照之前的思想来分析：

        个位是0，直接就是0了

        然后十位是4，后面位数是个位，个位的进制是2进制，也就是说，十位的1个数，需要个位的2个数。那么十位是4，就需要个位的  个数。

        最后是百位，后面的位数是十位，十位的进制是5进制，也就是说，百位的1个数，需要十位的5个数，那么百位是10，也就是需要  个十位的数，那么1个十位的数，需要2个各位的数，因此百位一共需要  个个位的数。

        因此这个X进制的321应该是 .

        剩下那个样例就留着大家自己推导。

---

        根据上面的推导，我们可以知道每一位对应的十进制数值，都跟后面的每一位的进制有关。

        因此，我们可以划出：

        黑色对应的从高到底每一位的数值，红色则是对应的进制。

       X进制转换成十进制就推导到这里，接下来解题。 

解题：

        说明一下贪心的原因，因为当对于两个数A,B,已知A>B,如A=111，B=100，如果进制越大，代表他们之间的差也就越大，如果A，B是20进制，那么它的值是421，B的值是400，差为20。

        如果A，B是2进制，那么他们之间的差值是7-4=3。

        因此，如果要求A和B之间的差值最小，那么他们可能的进制就要越小，因为每一位都不能超出X进制（因为一旦达到X，就要往前一位进1），因此，A的第i位和B的第i位，要选最小的可能的进制数，就需要求这两位中的最大值，然后+1，就是满足进制条件的最小可能的进制。

---

        对于100%的数据来说，A一定是大于B的，并且题目没有说A的位数和B的位数一致，那么根据A>=B,可以得知A的位数在一些数据之中是可以大于B的。

        因此我们需要对两个数组进行同样的长度扩展，B位不足的长度补0即可。

        A的长度位4，B的长度位3，则B在前面填充0，保持位数一致，如A= 4321，B=0321，这样就能满足位数相同了。

        但是我们拿数据的时候，是从高位到低位的，要是下标从0开始，那么这两个数组就成了：

        所以我们不能从0开始写入数据，也就是不能顺序写入数据到数组之中，要进行逆序写入，如： 

        A从Ma-1开始写入，B从Mb-1开始写入数据，这样就能保证他们的位数一致，我们接下来计算A-B，就可以直接从高位开始。

        这是我们假设一个C，C=A-B，那么C[i] = A[i]-B[i]* 后面所有位数的进制。

         这样的话每次都需要往后查找进制，很麻烦，我们就直接合并一下，得出：

        从高位向低位计算结果的时候：

        C[i] = ( C[i] *当前进制 + A[i]-B[i] ),初始状态，C[i] = 0,那么就不会计算当前位数的进制，只会记录当前位数的值，然后到下一位，就会用上一位的值，计算该位的进制。

        这里再拿例题中的10，4，0，说明一下

        首先令C为0，那么百位的10，是11进制，可以计算得出 0*11+10,当前的结果为10.

        然后再到十位，之前的C已经为10了，那么个位的十进制数是5，所以当前结果为10*5+4=54.

        最后才到个位，之前的C是54了，那么个位的值是0，十进制数是2，所以结果就是54*2+0 =108。

        至于为什么是这样，涉及到一个前缀和的推导，这里简单写一下:

        依旧是样例中的数据，10，4，0.

        10需要*5*2，

        4也需要*2，那么为什么不可以直接合并成(10*5+4)*2呢？

        再弄个大点的数吧，如A为 6 5 4 3 2 1 ，每一位的进制都是其本身+1。

        那么设十万位为A，则A=

        设万位为B，则B=

        设千位为C，则C=

        设百位为D，则D=

        设十位为E，则E=

        设个位为F，则F=1.

        那么这个数转换成十进制就应该是A+B+C+D+E+F，相当于：

        

        可以进行合并，如下： 

         可以得出推导公式为 

        因为题目求A-B，设C=A-B，那么Ci=Ai-Bi，因此推导也可以写成                                                   

        其中X为当前位的进制（通过贪心求出）。

AC代码(Java):

        因为这道题是C组的题，Java会被卡输入输出的，所以要用StreamTokenizer来接受数据：

import java.io.*;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    //要让A和B的差值最小，那么考虑贪心，局部最优解转换成全局最优解
    static final int MOD = 1000000007;
    static int M = 100000+10;
    static int[] A = new int[M];
    static int[] B = new int[M];

    //快速输入
    static StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    static int nextInt() throws IOException {
        st.nextToken();
        return (int) st.nval;
    }
    
    public static void main(String[] args) throws IOException {
        int n = nextInt();
        int ma = nextInt();
        for(int i = ma-1;i>=0;i--) {
            A[i] = nextInt();
        }
        int mb = nextInt();
        for(int i = mb-1;i>=0;i--) {
            B[i] = nextInt();
        }

        //记录最高的位数
        int m = Math.max(ma,mb);

        long ans = 0;
        //从高位遍历到低位
        for(int i = m-1;i>=0;i--) {
            //计算出当前最小的可能的进制
            int X = Math.max(A[i],B[i])+1;
            //需要保证最低进制必须位2，所以这里面也需要进行一下最小进制的判断
            X = Math.max(X,2);
            ans = (ans*X+A[i]-B[i])%MOD;
        }

        System.out.println(ans);
    }
}