stata简单回归与检验

stata简单回归与检验 – 潘登同学的stata笔记

OLS回归

sysuse auto, clear
regress price weight   // OLS

aaplot price weight    // 图示拟合情况

系数的t检验

// *-OLS 的估计系数是一个随机变量, SE 衡量了其不确定程度;

regress price weight
dis "t-value = " %4.2f _b[weight]/_se[weight]

twoway function y=tden(72, x),   ///
        rang(-6 6) xline(5.2, lp(dash) lc(red))

异方差稳健型标准误

sysuse auto, clear
reg price weight, robust

计算拟合值和残差

regress price weight
	
predict price_fit, xb  // 拟合值, xb 选项可以省略,默认
gen price_fit2 = _b[_cons] + _b[weight]*weight //手动计算

predict e, residual    // 残差, residual 选项是必须的, 可以简写为 r
gen e2 = price - price_fit //手动计算

br price weight price_* e*

残差分析

计算正常工资和超额工资
  
sysuse nlsw88, clear
        
global x "age hours tenure collgrad married south"
reg wage $x
keep if e(sample)   //仅保留参与回归的观察值, 参见 D3_miss.do
        
predict normal_wage       //正常工资(线性拟合值)
        
predict excess_wage, res  //超额工资(残差, 可正可负)
        
// *-进一步分析	  

histogram excess_wage     //直方图, 参见 G3_histogram.do
        
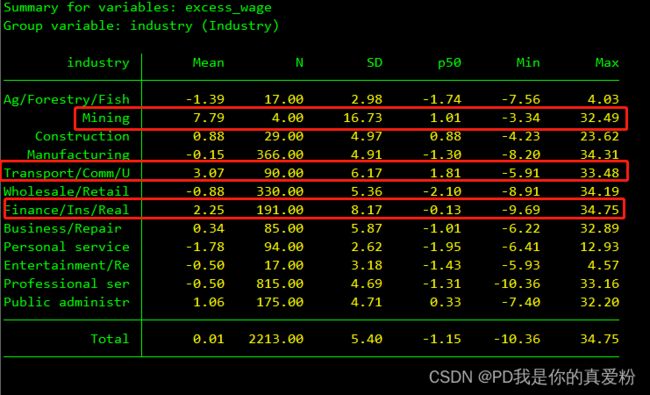
tabstat excess_wage, by(industry)  c(s)   /// //统计分析
        s(mean N sd p50 min max) f(%4.2f)
        
global z "i.race union never_married"	
reg excess_wage $z    //影响因素,不完整

相关系数矩阵

相关矩阵散点图

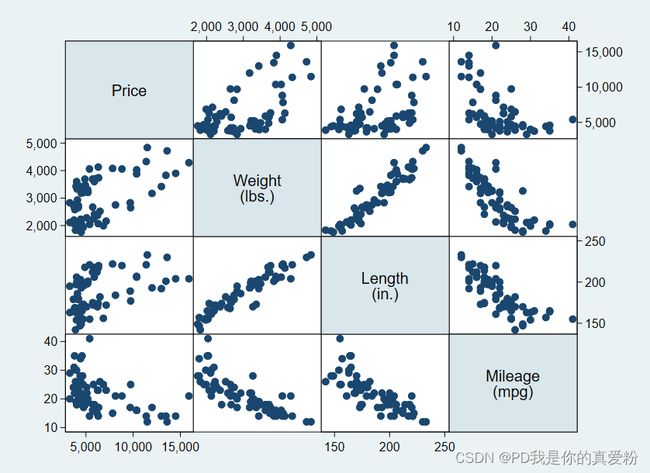
sysuse auto, clear
graph matrix price weight length mpg

Pearson 相关系数

sysuse nlsw88, clear

// *-stata 官方命令
global x "age grade wage hours ttl_exp tenure"
pwcorr $x      //缺陷: (1)小数点后两位为宜; (2)没有标注显著水平;
pwcorr $x, sig        //整理起来很麻烦
pwcorr $x, star(0.05) //小数点后两位不易调整;

// 自编命令 _a与_c的主要区别就是标星的时候a会根据显著性水平标1-3颗星
pwcorr_a $x, format(%7.3f)
pwcorr_c $x, star(0.05) format(%7.2f) //比较符合多数期刊的要求

Spearman 相关系数

sysuse nlsw88, clear

// *-stata 官方命令
global x "age grade wage hours ttl_exp tenure"
spearman $x, star(0.05)

Spearman 和 Pearson 相关系数矩阵的合并呈现

sysuse nlsw88, clear

// *-stata 官方命令
global x "age grade wage hours ttl_exp tenure"
corsp $x, format(%7.3f)
corsp $x, format(%7.3f) pvalue

注意：

• Pearson 相关系数, 下三角
• Spearman相关系数, 上三角
• 可以根据 p-value 自行添加星号,标注显著水平

Spearman 和 Pearson 相关系数的区别

• 连续变量, 正态分布, 线性关系. 二者均可, Pearson 相关系数较好;
• 上述任一条件不满足，用 spearman 相关系数，不能用 Pearson 相关系数

t检验

单变量t检验

sysuse nlsw88, clear
	
ttest wage, by(collgrad)  

ttest wage, by(race)            //错误命令
ttest wage if race!=3, by(race) //限定为两组即可

多变量t检验

本质上是多个单变量合并的结果

sysuse nlsw88, clear
global x "wage hours tenure ttl_exp" //待检验变量列表
ttable3 $x, by(collgrad)

normdiff 命令： 输出 t 值 或 p 值

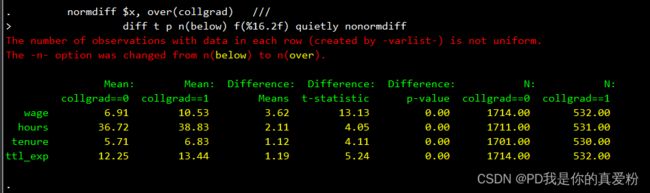
sysuse nlsw88, clear
global x "wage hours tenure ttl_exp" //待检验变量列表
normdiff $x, over(collgrad)   ///
        diff t p n(below) f(%16.2f) quietly nonormdiff

normdiff:标准化差异

sysuse nlsw88, clear
global x "wage hours tenure ttl_exp" //待检验变量列表
qui reg $x
keep if e(sample) //保证所有的变量有相同的观察值个数
normdiff $x, over(collgrad)   ///
            diff t p n(below) f(%16.2f) quietly

变量在多组之间的差异

本质上就是单变量运行多个分组合并的结果

sysuse nlsw88, clear
ttestplus wage, by(married union collgrad south)
// Group1: var=0; Group2: var=1

稳健型标准误

White 异方差稳健型标准误

sysuse nlsw88, clear
global x "ttl_exp race age industry hours"

reg wage $x
est store homo

reg wage $x, robust  // White(1980)
est store robust

esttab homo robust, mtitle(Homo Het_Robust) nogap

注意：

• 这是 90% 以上的文献都采用的方法；
• 后续复杂模型的稳健型标准误也基本上以 White(1980) 为基础

聚类调整后的标准误

思想：

• 同行业的个体的干扰项之间彼此相关
• 不同行业的个体的干扰项之间彼此不相关

sysuse nlsw88, clear
global x "ttl_exp race age industry hours"
reg wage $x, vce(cluster industry)

// 二维 cluster: industry occupation
  
egen indoccu = group(industry occupation) //D5_egen.do
sort industry occupation
br industry occupation indoccu

reg wage $x, vce(cluster indoccu)

自抽样法(Bootstrap)稳健型标准误

基本思想:假设样本是母体中随机抽取的,通过反复从样本中抽取样本来模拟母体的分布；

1. 采用 OLS 估计原始模型, 得到 $x$ 的估计系数 ${\beta }_x$
2. 从样本中有放回地抽取 N 个观察值，执行OLS，记录系数估计值
3. 将第2步重复进行 300 次，得到系数估计值的 300 个记录, 即${\beta }_j=\{{\beta }_1,{\beta }_2,...,{\beta }_{300}\}$；
4. 计算这 300个估计值的标准差 $sd({\beta }_j)=sd\{{\beta }_1,{\beta }_2,...,{\beta }_{300}\}$， 将其视为实际估计值 ${\beta }_x$ 的标准误, 即 $sd({\beta }_j)=se({\beta }_x)$
5. 计算 t 值: $t={\beta }_x/se({\beta }_x)$, 以及相应的 p 值

reg wage hours, vce(bs,reps(300) noheader nodots) 
reg wage hours, robust noheader // White s.e.

注意：

1. 多数情况下，1000 次可重复抽样即可获得非常稳定的结果
2. stata 中的多数命令都支持 vce(bs) 选项
3. 投稿前, 请设定种子值, 以保证结果可以重现

reg price weight, vce(bs,reps(1000) seed(13579))

结果的呈现与输出

• regfit: 输出线性拟合表达式

reg price weight length mpg trunk i.foreign i.rep78
regfit
dis in g "R-square = " in y %4.2f e(r2) in g "  F = " in y %4.2f e(F)

• ereturn回归后的返回值

reg price weight length mpg trunk i.foreign i.rep78
ereturn list 

• logout将结果输出到文档中

// 调入数据
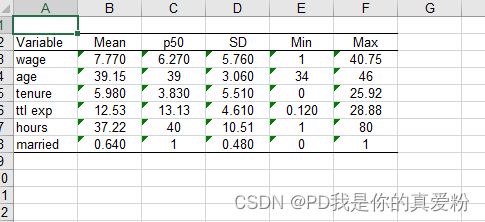
sysuse nlsw88.dta, clear
 
global xx "wage age tenure ttl_exp hours married"
logout, save("Tab1_statis") excel replace: ///
tabstat $xx, stat(mean p50 sd min max)   ///
                        format(%3.2f) column(statis)

• est store暂存结果
• esttab 将暂存结果显示

// 调入数据
sysuse nlsw88.dta, clear
 
global xx "wage age tenure ttl_exp hours married"
reg $xx
est store full
reg $xx if race==1
est store white
reg $xx if race==2
est store black
reg $xx i.occupation
est store occu

esttab full white black occu, nogap // 基本设定

// 接上面
// local s "using Tab3_reg.csv"    // 输出 Excel 文档的暂元
local m "full white black occu" // 放置模型名称的暂元 
// esttab `m' `s', nogap compress replace 能直接输出到csv文档中
esttab `m' , nogap compress             ///
        mtitle("Full" "White" "Black" "with_occu") ///
        b(%4.3f) t(%4.2f)                          /// 
                scalar(N r2_a)                             ///
                star(* 0.1 ** 0.05 *** 0.01)               ///
                drop(*.*)

其中：

• nogap 去掉空行
• compress 以比较紧凑的形式呈现结果
• replace 覆盖已经存在的旧文件
• b(%4.3f) 系数保留小数点后三位
• t(%4.2f) t 值保留小数点后两位
• scalar() 最后两行的统计量: N-样本数; r2_a-adj-R2