Strange display

这个题一道区间覆盖题:

这里要用到线性规划：

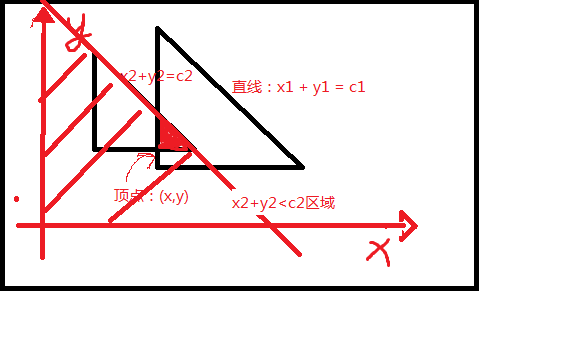
max（x , xi），max(y,yi)寻找顶点坐标；

min(c , ci) 寻找最下的区域；

因此:r = c - x - y;

View Code

View Code 

#include<cstdio>

#include<cstdlib>

#include<cmath>

#include<algorithm>

#define LL long long

using namespace std;

LL sum;

int X[15],Y[15],R[15],C[15],n;

void Solve( int x , int y , int  floor , int c , int kol , int sign )

{

     //floor表示递归的层数，kol表示重合的个数，sign表示黑白区间；

     //c表示一条直线 x + y + c = 0; 

     if( x + y >= c ) return ;//x,y不在区间内 

     if( floor == n )

     {

         if( kol == 0 ) return;

         LL r = c - x - y;

         sum += sign*( 1LL<<(kol-1) )*r*r;

         return ;        

     }    

     Solve( x , y , floor + 1, c, kol , sign );//不选这个三角形 

     //选取这个三角形； max 选取最大的x与y做顶点，min选取划定区间的直线 

     Solve( max( x , X[floor] ) , max( y , Y[floor] ), floor + 1, min( c , C[floor] ), kol+1 , -sign );

}

int main( )

{

    while( scanf( "%d",&n )==1 )

    {

        sum = 0LL;

        for( int i = 0 ; i < n ; i ++ )

        {

             scanf( "%d %d %d",&X[i],&Y[i],&R[i] );

             C[i] = X[i] + Y[i] + R[i]; //直线 x + y + c = 0； 

        }

        Solve( 0 , 0 , 0,  1000000000 , 0 ,-1  );

        printf( "%I64d.%I64d\n",sum/2,sum&1?5LL:0LL );

    }

    return 0;

}