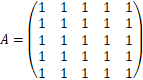Python实现奇异值分解（SVD）压缩图片

奇异值分解(Singular Value Decomposition 简称SVD)是线性代数中的一种重要分解，在很多领域都有着广泛的应用。这篇文章将通过一个图像压缩的例子教你如何在Python中使用SVD实现数据压缩，并说明其原理。

奇异值分解压缩的原理

先看一个简单的例子，如果你想要在网络上给别人发送一段数据，数据的内容为

当然，最简单的方法就是给这个矩阵直接发过去，这是一个5x5的矩阵，你至少需要发送25个数字。

但是我们可以把这个矩阵分解为两个矩阵的乘积，这样只需要发送10个数字。

图像也可以被视为矩阵，图像的每一个点都是由RGB值定义的，所以每个图像可以被表示为三个巨型矩阵（分别是R，G，B矩阵）。

但图像所生成的矩阵显然不会像上面的例子那样简单的就被分解了。想要分解任意矩阵，这就需要用到SVD了。

SVD分解可以被认为是EVD（Eigen Value Decomposition 特征值分解）的延伸。特征值分解将一个矩阵分解为两组正交的特征向量和一个特征值对角线矩阵。

而特征值矩阵又是从大到小排列的，特征值大小的下降速度很快，我们可以通过丢弃一些特征值来压缩数据。对于压缩图像来说，只要人眼不可察觉便可以认为是成功的压缩。

简单来说，就是通过把一块大的数据分解为很多项，通过给数据的每个项的重要程度排序，挑选出一部分最重要的保留，丢弃一部分最不重要的，来实现数据压缩。

Python实现图像压缩

在python中使用SVD算法很容易，直接使用库函数即可。这里主要使用numpy库用来进行矩阵计算，matplotlib用来显示图像以及PIL库用来读取本地测试图片。

首先需要把测试图片导入进来，转换为numpy的矩阵。

img=Image.open(,)
a=np.array(img)

 

这里图片转矩阵后的格式实际上是一个图片长乘宽的矩阵，这个矩阵的每一个项都包含3个数字，分别是R,G,B的值

实现SVD分解

SVD分解只需要一句话即可

u,sigma,v=np.linalg.svd(a[:,:,0])

这里的SVD分解返回三个执行后返回三个矩阵，分别是u,sigma和v

实现重建函数

def rebuild_img(u,sigma,v,p):
     m=len(u)
     n=len(v)
     a=np.zeros((m,n))
 
     count=(int)(sum(sigma))
     curSum=0
     k=0
 
     while curSum<=count*p:
         uk=u[:,k].reshape(m,1)
         vk=v[k].reshape(1,n)
         a+=sigma[k]*np.dot(uk,vk)
         curSum+=sigma[k]
         k+=1
 
     a[a<0]=0
     a[a>255]=255
    
     return np.rint(a).astype()

重建函数接受4个参数，u,sigma,v即重建矩阵所需的内容，p则为使用特征值的比例，我们将通过改变比例p来看使用特征值比例对画面的影响。

算法的步骤如下描述：

首先计算出m和n，即图片矩阵的长和宽，然后创建一个零矩阵a作为组装场地。

count是所有特征值加起来的总和，用于后面计算比例使用

uk和vk就是从参数u和v中取出，改变形式后形成的与当前特征值对应得一组特征向量。

然后不断地从参数中取出uk、vk和sigma，运算后叠加到a上去，直到满足一定的比例。

最后把所有矩阵内的项取整数退出即可。

数据压缩实验

有了分解与重建，现在可以设计数据压缩试验了。

这里我们控制特征值的使用比例，从0.1到1，每次步进0.1，然后分解重建，看看图像的显示情况。

for i in np.arange(0.1,1,0.1):
     u,sigma,v=np.linalg.svd(a[:,:,0])
     R=rebuild_img(u,sigma,v,i)
 
     u,sigma,v=np.linalg.svd(a[:,:,1])
     G=rebuild_img(u,sigma,v,i)
 
     u,sigma,v=np.linalg.svd(a[:,:,2])
     B=rebuild_img(u,sigma,v,i)
 
     I=np.stack((R,G,B),2)
     plt.subplot(330+i*10)
     plt.title(i)
     plt.imshow(I)
 
 plt.show()

为了展示细节的丢失程度，特地找了一张细节丰富的图像作为试验对象。原图分辨率1920×724,见图1.

 

                                                  图 1    丰富细节的原始图

图2为运行结果

                                                  图 2     SVD分解后结果图

可以看到，当sigma比例在0.5及以下时，能够明显察觉到图片被压缩的痕迹，但当sigma比例超过0.6时，细节的还原就比较好了，当0.7,0.8,0.9时，肉眼几乎无法发现压缩痕迹，证明了SVD作为图像压缩算法，在细节丢失方面是可以控制得比较好的。在保持细节的前提下，可以将数据压缩10%-30%左右。

最后，如果您有python /java /小程序/安卓/linux相关需求，可以通过微信公众号联系我们。

微信公众号：320科技工作室。