树的直径问题

一，定义

树的直径就树中所有最短路经距离的最大值

求取树的直径可以使用两遍dfs或者树形dp获得

二，两遍dfs获得树的直径（注意，该方法边权必须都为正边权）

思路：

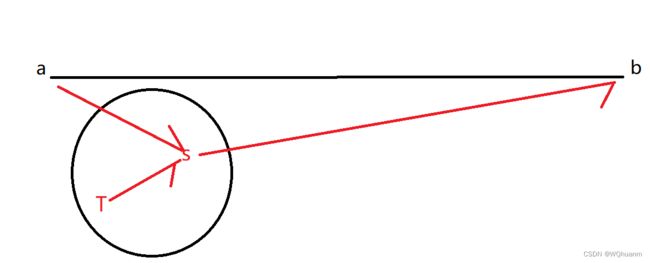
我们首先任取一点走dfs，然后拿深度最深的点a（必为直径的端点）为root再做一遍dfs，此时获得的最深深度就是树的直径（离直径端点最远的点当然是直径的另一端点）

证明：

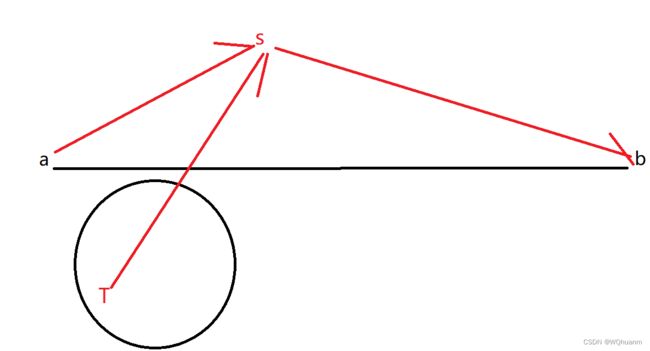
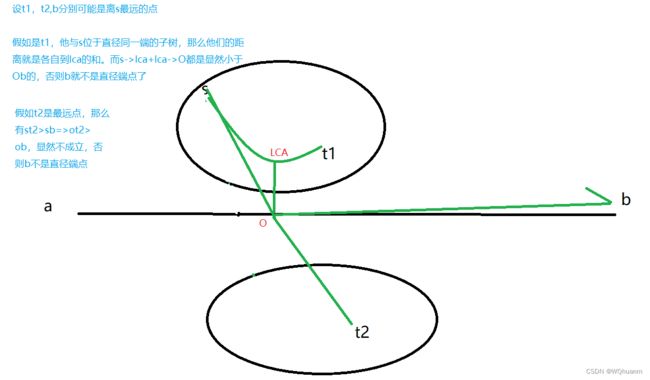
1. 如果s在ab上，假如遍历后深度最深不是a，而是t，那么有ts>as=>tb>ab(直径），不成立

如果s不在直径上

 

1. 当t与s在一块时，那么有ts>as=>tb>ab,仍然不成立
2. 
3. 当t与s不在一块 ，最深不是a而是t，还是有ts>as=>tb>ab,不成立
4. 
5.  综上，a必定是直径端点

三，树形dp

思路：

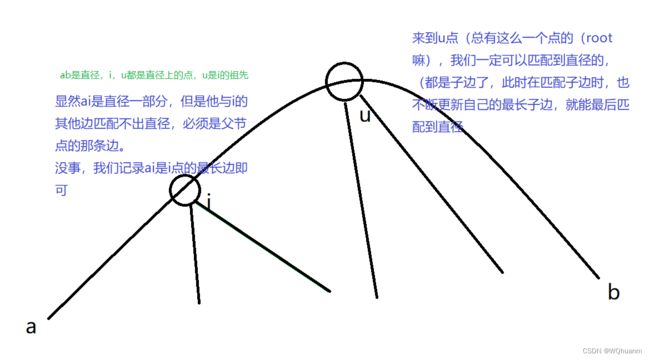
我们用len[i]数组存储i为根节点时，他的最长边，显然当i是直径端点时，len[i]就是直径，当i是直径上的点时，他的最长边必定是直径的一部分，另一部分就是他连接的其他边的其中一条（或者多条），匹配一下更新最长直径即可。具体如下图

代码看下面例题即可，两道各用一种方法 

例题一：Problem - 2196 (hdu.edu.cn)

思路：

求每个点的最长距离，先说结论，每个点的最远距离点一定是直径端点。

 所以我们两遍dfs求出树直径，那么第三遍从直径另一端点出发遍历，显然每个点的最远距离就是到其中一个端点的距离

#include 
using namespace std;
#define ll               long long
#define endl             "\n"
typedef pair pii;
const int N = 2e5 + 10;

vectoredge[N];

void dfs(int u,int f,int w,vector&dis)
{
	dis[u]=dis[f]+w;
	for( pii k:edge[u])if(k.first!=f)dfs(k.first,u,k.second,dis);
}

void mysolve()
{
	int n;
	while(cin>>n)
		{
			int x,y;
			for(int i=1; i<=n; ++i)edge[i].clear();
			for(int i=2; i<=n; ++i)cin>>x>>y,edge[i].push_back({x,y}),edge[x].push_back({i,y});
			vectordis1(n+1),dis2(n+1);
			dfs(1,0,0,dis1);//第一遍dfs确定第一个直径端点
			int a=max_element(dis1.begin()+1,dis1.end())-dis1.begin();
			dfs(a,0,0,dis1);//第二遍dfs确定直径另一个端点
			int b=max_element(dis1.begin()+1,dis1.end())-dis1.begin();
			dfs(b,0,0,dis2);//从另一个端点出发，每个点的最远距离就是到两个端点的最大值
			for(int i=1; i<=n; ++i)cout<> t;
	while (t--)
		{
			mysolve();
		}
	system("pause");
	return 0;
}

例题二：Problem - 3534 (hdu.edu.cn)

思路：

我们用dp求，增添一个记录路径数的数组num。每次更新最长路径的时候更新该路径的路径数即可

#include 
using namespace std;
#define ll               long long
#define endl             "\n"
typedef pair pii;
const int N = 2e5 + 10;
vectoredge[N];
		
int len[N],num[N],ans,sum;
		
void dfs(int u,int f)
{
	len[u]=0,num[u]=1;
	for(pii k:edge[u])if(k.first!=f)
			{
				int v=k.first;
				dfs(v,u);
				int tmp=k.second+len[v];
				if(tmp+len[u]>ans)ans=tmp+len[u],sum=num[u]*num[v];//如果更新最长（待定）直径或者最长（待定）路径，顺便更新其数量
				else if(tmp+len[u]==ans)sum+=num[u]*num[v];
				if(tmp>len[u])len[u]=tmp,num[u]=num[v];
				else if(tmp==len[u])num[u]+=num[v];
			}
}
		
void mysolve()
{
	int n;
	while(cin>>n)
		{
			for(int i=1; i<=n; ++i)edge[i].clear();
			int x,y,w;
			for(int i=1; i>x>>y>>w,edge[x].push_back({y,w}),edge[y].push_back({x,w});
			ans=sum=0;
			dfs(1,0);
			cout<> t;
	while (t--)
		{
			mysolve();
		}
	system("pause");
	return 0;
}